Kreisgleichung
In diesem Artikel erklären wir dir die Kreisgleichung und zeigen dir anhand eines Beispiels, wie du sie aufstellen kannst. Des Weiteren gehen wir mittels der Kreisfunktion auf die Lage von Punkten im Kreis und auf den Schnitt von Kreisen ein.
Du möchtest wissen, was die Kreisgleichung genau ist? Dann schau dir unser Video dazu an.
Inhaltsübersicht
Kreisgleichung einfach erklärt
Ein Kreis mit Radius  und Mittelpunkt
und Mittelpunkt  ist allgemein als die Menge aller Punkte definiert, die den Abstand
ist allgemein als die Menge aller Punkte definiert, die den Abstand  zum Mittelpunkt
zum Mittelpunkt 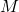 besitzen. Ein solcher Kreis beziehungsweise die Punkte auf dem Kreis lassen sich mit einer sogenannten Kreisgleichung beschreiben. Für diese gibt es zwei Arten der Darstellung:
besitzen. Ein solcher Kreis beziehungsweise die Punkte auf dem Kreis lassen sich mit einer sogenannten Kreisgleichung beschreiben. Für diese gibt es zwei Arten der Darstellung:
Normalform:

Parameterform:


Kreisgleichung in Normalform
Die Kreisgleichung

beschreibt einen Kreis mit Radius  um den Ursprung. Diese Formel ergibt sich aus dem Satz des Pythagoras. Denn die Strecken der Ortskoordinaten
um den Ursprung. Diese Formel ergibt sich aus dem Satz des Pythagoras. Denn die Strecken der Ortskoordinaten  und
und  eines jeden Punktes
eines jeden Punktes  auf dem Kreis bilden zusammen mit dem Ortsvektor
auf dem Kreis bilden zusammen mit dem Ortsvektor  ein rechtwinkliges Dreieck.
ein rechtwinkliges Dreieck.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Kreisgleichung in Parameterform
Bei der Parameterdarstellung betrachtet man neben dem Radius noch einen weiteren Parameter, den Winkel  . Dieser ermöglicht es uns die Koordinaten
. Dieser ermöglicht es uns die Koordinaten  und
und  unabhängig von einander anhand der sogenannten Polarkoordinaten
unabhängig von einander anhand der sogenannten Polarkoordinaten
 darzustellen:
darzustellen:


Sie beschreiben einen Kreis mit Radius  um den Ursprung (
um den Ursprung ( und
und  ). Um diese Darstellung zu verstehen, betrachten wir den Einheitskreis mit
). Um diese Darstellung zu verstehen, betrachten wir den Einheitskreis mit  . Zeichnet man den Ortsvektor
. Zeichnet man den Ortsvektor

eines Punktes auf dem Einheitskreis, so beschreibt  den Winkel, den dieser ausgehend von der positiven x-Achse gegen den Uhrzeigersinn zurücklegt. Mit
den Winkel, den dieser ausgehend von der positiven x-Achse gegen den Uhrzeigersinn zurücklegt. Mit  können wir nun den Ortsvektor
können wir nun den Ortsvektor 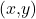 bestimmen, dessen Spitze auf dem Kreis mit Radius
bestimmen, dessen Spitze auf dem Kreis mit Radius  um den Ursprung liegt.
um den Ursprung liegt.  gibt uns bereits die Richtung an, in welche der Vektor
gibt uns bereits die Richtung an, in welche der Vektor 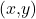 zeigt. Damit die Spitze des Vektors
zeigt. Damit die Spitze des Vektors 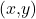 tatsächlich auf dem Kreis mit Radius
tatsächlich auf dem Kreis mit Radius  liegt, muss
liegt, muss  entsprechend um den Faktor
entsprechend um den Faktor  gestreckt bzw. gestaucht werden. Das Ergebnis ist der gesuchte Ortsvektor
gestreckt bzw. gestaucht werden. Das Ergebnis ist der gesuchte Ortsvektor 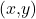 auf dem Kreis mit Radius
auf dem Kreis mit Radius 

Kreisgleichung aufstellen
Im folgenden zeigen wir, wie du eine Kreisgleichung aufstellen kannst. Gegeben sei der Mittelpunkt 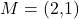 eines Kreises, sowie ein Punkt
eines Kreises, sowie ein Punkt  , welcher auf dem Kreis liegt. Bestimme nun seine Kreisgleichung in Normalform.
, welcher auf dem Kreis liegt. Bestimme nun seine Kreisgleichung in Normalform.
Wir haben die Koordinaten des Mittelpunktes  und
und  bereits gegeben. Um die Gleichung aufstellen zu können, müssen wir daher lediglich den Radius
bereits gegeben. Um die Gleichung aufstellen zu können, müssen wir daher lediglich den Radius  berechnen.
berechnen.
Wir wissen, dass ein Kreis mit Mittelpunkt 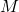 und Radius
und Radius  definiert ist als die Menge aller Punkte, welche den Abstand
definiert ist als die Menge aller Punkte, welche den Abstand  zum Punkt
zum Punkt 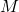 besitzen. Damit können wir
besitzen. Damit können wir  bestimmen, indem wir den Abstand des Punktes
bestimmen, indem wir den Abstand des Punktes  , welcher auf dem Kreis liegt, zum Mittelpunkt
, welcher auf dem Kreis liegt, zum Mittelpunkt 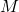 berechnen. Das heißt gesucht ist die Länge der Strecke
berechnen. Das heißt gesucht ist die Länge der Strecke 
Wir berechnen also zunächst  :
:

und anschließend die Länge des Vektors  :
:

Damit ergibt sich schließlich der Radius  . Setzt man nun
. Setzt man nun  , sowie
, sowie  und
und  in die Kreisgleichung ein, erhält man:
in die Kreisgleichung ein, erhält man:

Kreisfunktion und Lage im Kreis
Wir wissen nun, was eine Kreisgleichung ist und wie sie aufgestellt wird. Jetzt können wir sie verwenden, um die Lage eines Punktes  im Kreis zu untersuchen. Dafür betrachten wir die Kreisfunktion
im Kreis zu untersuchen. Dafür betrachten wir die Kreisfunktion

eines Kreises mit Mittelpunkt  . Der Kreis habe den Radius
. Der Kreis habe den Radius  .
.
Nun setzen wir den Punkt  in die Kreisfunktion
in die Kreisfunktion  ein, um herauszufinden, ob er innerhalb des Kreises, auf dem Kreis oder außerhalb des Kreises liegt. Gilt für die Funktion
ein, um herauszufinden, ob er innerhalb des Kreises, auf dem Kreis oder außerhalb des Kreises liegt. Gilt für die Funktion

so befindet sich der Punkt im Inneren des Kreises.
Ist hingegen

dann liegt der Punkt genau auf dem Kreis. Dementsprechend befindet sich der Punkt außerhalb des Kreises, wenn

Beispiel
Betrachten wir noch einmal unser Beispiel vom Aufstellen einer Kreisgleichung. Dort ist die Kreisfunktion durch

gegeben. Den Radius  haben wir bereits bestimmt. Nun wollen wir die Lage des Punktes
haben wir bereits bestimmt. Nun wollen wir die Lage des Punktes  untersuchen. Dafür setzen wir (3,-2) in die Kreisfunktion
untersuchen. Dafür setzen wir (3,-2) in die Kreisfunktion  ein:
ein:

Jetzt vergleichen wir dieses Ergebnis mit  Es gilt
Es gilt

somit liegt der Punkt  außerhalb des Kreises.
außerhalb des Kreises.
Kreisgleichung — häufigste Fragen
(ausklappen)
Kreisgleichung — häufigste Fragen
(ausklappen)-
Was bedeuten Mittelpunkt und Radius in der Kreisgleichung?Mittelpunkt und Radius in der Kreisgleichung geben an, wo der Kreis liegt und wie groß er ist:
 ist der feste Punkt im Zentrum und
ist der feste Punkt im Zentrum und  ist der Abstand jedes Kreispunkts zu diesem Mittelpunkt. In der Normalform
ist der Abstand jedes Kreispunkts zu diesem Mittelpunkt. In der Normalform  stehen
stehen  und
und  genau dafür.
genau dafür.
-
Wie erkenne ich an der Normalform den Mittelpunkt?Den Mittelpunkt erkennst du in der Normalform daran, dass er direkt in den Klammern steht: Aus
 liest du
liest du  ab. Beispiel: Bei
ab. Beispiel: Bei  ist der Mittelpunkt
ist der Mittelpunkt  .
.
-
Wann nutze ich die Parameterform statt der Normalform?Die Parameterform nutzt man, wenn man Kreispunkte über den Winkel
 beschreiben will, also
beschreiben will, also  und
und  . Damit lassen sich die Koordinaten über Polarkoordinaten
. Damit lassen sich die Koordinaten über Polarkoordinaten  angeben. Beispiel: Für den Einheitskreis gilt
angeben. Beispiel: Für den Einheitskreis gilt  und
und  .
.
-
Wie berechne ich den Radius aus Mittelpunkt und einem Kreispunkt?Den Radius berechnest du als Abstand zwischen Mittelpunkt
 und einem Punkt
und einem Punkt  , der auf dem Kreis liegt, also als Länge des Vektors
, der auf dem Kreis liegt, also als Länge des Vektors  . Beispiel: Für
. Beispiel: Für  und
und  ist
ist  und
und  .
.
-
Wie prüfe ich mit der Kreisfunktion die Lage eines Punktes?Mit der Kreisfunktion
 setzt man den Punkt
setzt man den Punkt  ein und vergleicht mit
ein und vergleicht mit  :
:  innen,
innen,  auf dem Kreis,
auf dem Kreis,  außen.
außen.
Schnittpunkt zweier Kreise
Wir wollen nun untersuchen, ob sich zwei Kreise schneiden und falls ja, wie viele Schnittpunkte es gibt. Dafür betrachten wir den Abstand der Mittelpunkte im Vergleich zur Summe der Radien.
Gegeben seien zwei Kreise mit Mittelpunkten  und
und  und Radien
und Radien  und
und  .
.
Der Abstand der Mittelpunkte wird folgendermaßen berechnet:

Nun vergleichen wir ihn mit der Summe der Radien:  .
.
Ist der Abstand der Mittelpunkte größer als die Summe der Radien, also

dann schneiden sich die Kreise nicht.
Gilt Gleicheit, das heißt

dann besitzen die Kreise einen Berührpunkt.
Wenn hingegen die Summe der Radien größer ist als 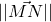

dann besitzen die Kreise zwei Schnittpunkte.

