Kontextfreie Grammatik
Du möchtest wissen was es mit der kontextfreien Grammatik auf sich hat? Neben der allgemeinen Definition erfährst du hier und in unserem Video , wie man kontextfreie Grammatik erstellen kann mittels einem kontextfreie Grammatik Beispiel! Zusätzlich zeigen wir dir auch alle wichtigen Punkte über kontextfreie Sprachen und deren Beweis.
Inhaltsübersicht
Kontextfreie Grammatiken
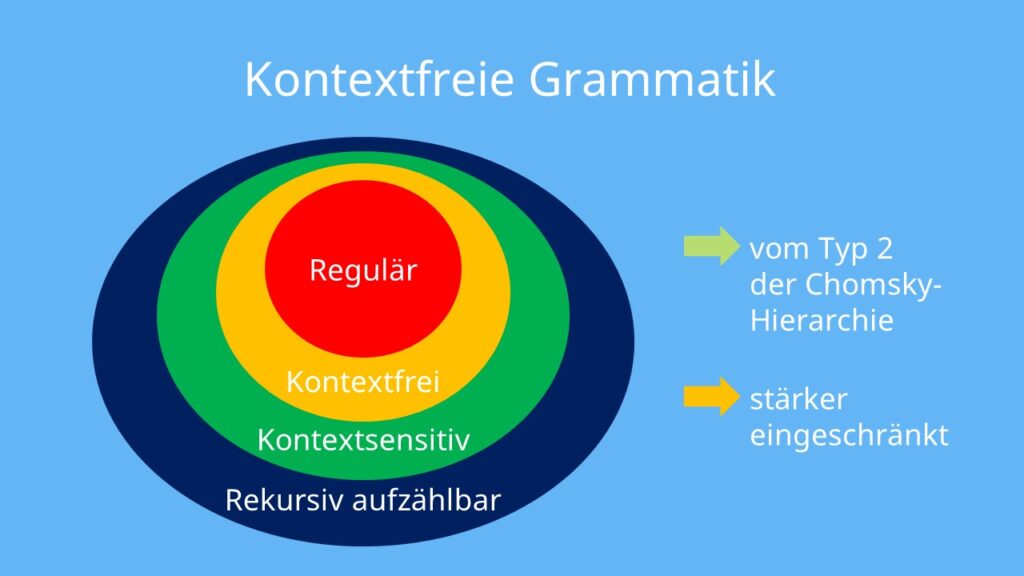
Eine kontextfreie Grammatik beschreibt kontextfreie Sprachen in der theoretischen Informatik. Es ist ein 4-Tupel (V, T, P, S) bestehend aus Vokabular, Terminalsymbolen, Produktionsregeln und einem Startsymbol. Kontextfreie Grammatiken sind dabei deckungsgleich mit der Typ-2-Grammatik der Chomsky-Hierarchie.
Formale Definition
Die kontextfreie Grammatik definiert sich wie folgt:

- Ein endliches Vokabular V
- Das Vokabular besteht aus Terminalsymbolen T mit der zugehörigen Differenzmenge von Nichtterminalsymbolen. Beide bilden disjunkte Teilmengen von V. Das heißt nichts anderes, als dass ein Nichtterminal keine Variable sein kann und umgekehrt.


- Das Startsymbol S darf ebenfalls nicht fehlen und stellt dabei natürlich eine Variable dar.
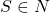
- Am wichtigsten sind aber die Produktionsregeln P. Diese werden benutzt, um sogenannte Satzformeln und Wörter abzuleiten. Dabei gilt, dass eine kontextfreie Grammatik als kontextfrei bezeichnet wird, weil auf der linken Seite der Produktionsregel nur genau eine Variable stehen darf. Deswegen kann die Variable unabhängig von ihrer aktuellen Umgebung, nach den Regeln auf der rechten Seite ersetzt werden. Auf der rechten Seite darf eine beliebige Folge aus Terminalen und Nichtterminalen stehen.


Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Kontextfreie Grammatik erstellen
Mit Hilfe dieser Regeln kann man eine kontextfreie Grammatik erstellen, die beispielsweise die Sprache der Palindrome erzeugen kann. Zur Vereinfachung werden im Folgenden dabei nur die Buchstaben x und u verwenden.

Diese eine Produktionsregel genügt bereits, um die Sprache zu erzeugen.

Dadurch kann exemplarisch das Wort „xxuxuxx“ Schritt für Schritt entstehen:
 xx
xx
 xxxx
xxxx
 xxuuxx
xxuuxx
 xxuxuxx
xxuxuxx
Mit einer regulären Grammatik lässt sich die Sprache übrigens nicht erzeugen können, in diesem Video erfährst du wieso.
Kontextfreie Grammatik Beispiel
Eine Grammatik, die die Syntax einer Programmiersprache überprüft, ist natürlich zu komplex. Aber wie wäre es mit einem vereinfachten Taschenrechner? Eine passende Grammatik überprüft dabei das korrekte Setzen der Klammern.
Das folgende kontextfreie Grammatik Beispiel, soll diesen Term generieren:

Im weiteren Verlauf soll eine Grammatik also so entwickelt werden, die diesen Term generieren kann:

Dafür benötigen wir als Terminale die mathematischen Operationen und die Symbole für die Zahlen. Außerdem benötigt man noch Nichtterminale.


Produktionsregeln, nach denen auf der linken Seite der Gleichung nur eine Zahl stehen darf und auf der rechten Seite eine beliebige Kombination aus Klammern, Plus- und Minusoperationen, könnten dann so aussehen:



Im nächsten Schritt folgt eine Überprüfung des arithmetischen Ausdrucks:









Das Startsymbol lässt uns zunächst keine Wahl. Danach verwandeln wir A zuerst in y und dann B in B minus B. Jetzt müssen wir die Klammern erzeugen, erst beim linken B und dann beim rechten. Mit der bereits verwendeten Ableitungsregel erzeugen wir dann noch die Ausdrücke in den Klammern und können zum Schluss die einzelnen Variablen ersetzen.
Durch die Regel können auch keine irregulären Zeichenfolgen wie ** oder (() erzeugt werden.
Ableitungsbaum
Für die Untersuchung, ob ein Wort tatsächlich in einer Sprache enthalten ist, benutzt man beispielsweise einen Ableitungsbaums bzw. Parse-Tree. Ein Parser erzeugt genau solche Ableitungsbäume.
Das kontextfreie Grammatik Beispiel wird im Folgenden als Ableitungsbaum dargestellt:
Das Startsymbol bildet die Wurzel. Die linke und rechte Variable werden entsprechen als Kind ihrer jeweiligen Seite eingefügt. Dazwischen wird in der selben Ebene das Terminal eingesetzt. In die nächste Ebene kommt dann sowohl die Umwandlung von A in y als auch die von B in B plus B. Im Anschluss werden Klammern um die Nichtterminale erzeugt und mit den entsprechenden Ausdrücken gefüllt. Im letzten Schritt werden dann die Variablen n die letzten Terminale überführt.
Wenn sich der Parser jetzt vom Startsymbol aus entgegen des Uhrzeigers durch den Baum arbeitet und alle Terminale aufschreibt, erhält man zum Schluss die Rechnung.
Kontextfreie Sprache
Die kontextfreie Sprache ist eine formale Sprache in der theoretischen Informatik. Sie wird von der kontextfreien Grammatik erzeugt und wird entsprechend auch durch sie nachgewiesen. Diese werden in der Informatik hauptsächlich benötigt, da sie im Gegensatz zu regulären Grammatiken auch Klammerstrukturen zulassen. Der Ausdruck einer kontextfreien Sprache muss deshalb den Regeln der Grammatik entsprechen. Das bedeutet, dass eine kontextfreie Sprache auch wortwörtlich vom Kontext unabhängig ist.
Kontextfreie Sprache Eigenschaften
Kontextfreie Sprachen sind Typ-2-Sprachen der Sprachklasse der Chomsky-Hierarchie . Dabei besitzt eine kontextfreie Sprache Klasse die reguläre Sprache vom Typ 3 und wir dabei gleichzeitig von der kontextsensitiven Sprache vom Typ 1 umfasst.
Dabei besitzt die Kontextfreie Sprache die folgenden Eigenschaften, wenn ihre Klasse als abgeschlossen gilt:
- Vereinigung
- Verkettung
- Spiegelungen
- Homomorphismen
- Schnitt mit regulären Sprachen
Hingegen im Fall eines Durschnitts oder Komplements gilt eine kontextfreie Sprache als nicht abgeschlossen.
Kontextfreie Sprache Beweis
Eine kontextfreie Sprache lässt sich durch ein spezielles Pumping Lemma beweisen.
Liegt eine Grammatik in Chomsky Normalform vor, kann zusätzlich nachgewiesen werden, wenn die Grammatik nicht kontextfrei ist. Dafür verwendet man das Pumping Lemma für kontextfreie Sprachen, das vom Grundprinzip her ähnlich funktioniert wie das Pumping Lemma für reguläre Sprachen. Mehr dazu in den Videos „Pumping Lemma kontextfreie Sprache“ und „Pumping Lemma reguläre Sprache
“.
Chomsky Normalform
Mit dem CYK-Algorithmus kann zu jeder kontextfreien Grammatik ein Parser generiert werden, der das Wortproblem löst. Voraussetzung dafür ist, dass die Sprache zunächst in eine formalere Form überführt wird: Die Chomsky Normalform, abgekürzt auch als CNF bekannt. Diese schränkt die Regeln für kontextfreie Grammatiken auf der rechten Seite ein. Dennoch kann damit jede kontextfreie Sprache generiert werden. Wie genau funktioniert, was es mit dem CYK-Algorithmus auf sich hat und welche Normalformen es noch für kontextfreie Grammatiken gibt, erfährst du in diesem Video.
Greibach Normalform
Die Greibach-Normalform beschreibt eine Normalform der kontextfreien Grammatik. Dabei gilt, dass eine kontextfreie Grammatik, nach der nicht der leere Ausdruck abgeitet werden kann, in eine Greibach-Normalform umgewandelt werden kann. Dabei gilt, dass die rechten Seiten der Regeln immer mit einem Terminalzeichen beginnt, gefolgt von beliebig vielen Variablen. Dadurch wird die Ausdrucksstärke der Grammatik nicht eingeschränkt.