Ansatz vom Typ der rechten Seite / Störfunktion
Du möchtest wissen, wie der Ansatz vom Typ der rechten Seite funktioniert? Dann zeigen wir dir hier, wie du lineare Differentialgleichungen mit dieser Methode lösen kannst, an einfachen Beispielen.
Inhaltsübersicht
Ansatz vom Typ der rechten Seite
Du hast bereits die Methode der Variation der Konstanten kennengelernt. Diese kannst du bei allen linearen Differentialgleichungen anwenden. Sie ist also sehr praktisch. Dennoch musst du einmal integrieren. Integrieren kann manchmal sehr aufwendig sein. Daher gibt es den Ansatz vom Typ der rechten Seite, der auch als Ansatz vom Typ der Störfunktion bezeichnet wird. Somit ist es zu empfehlen, die Störfunktion der DGL zunächst einmal anzuschauen. Viele Differentialgleichungen kannst du nämlich mit dieser Methode lösen. Aber Achtung, das ist nur möglich, wenn deine DGL eine lineare Differentialgleichung mit konstanten Koeffizienten ist.
Ist dein inhomogener Anteil ein Polynom, eine trigonometrische Funktion, eine Exponentialfunktion oder gar eine Kombination aus diesen Typen, kannst du für die Partikulärlösung einen Ansatz vom Typ der Störfunktion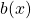 
wählen. Dabei hat dein Ansatz die gleiche Bauart, wie die rechte Seite der DGL.
Beispiel 1
Für unser Beispiel wählen wir folgende Differentialgleichung:
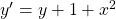
Sie eignet sich für diese Methode, denn die DGL ist linear mit konstanten Koeffizienten. Jetzt schaust du dir die Störfunktion 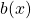genau an. Im Beispiel ist 
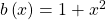und damit ein Polynom zweiten Grades. Somit darfst du als partikuläre Lösung einen Ansatz vom Typ der rechten Seite,
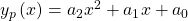
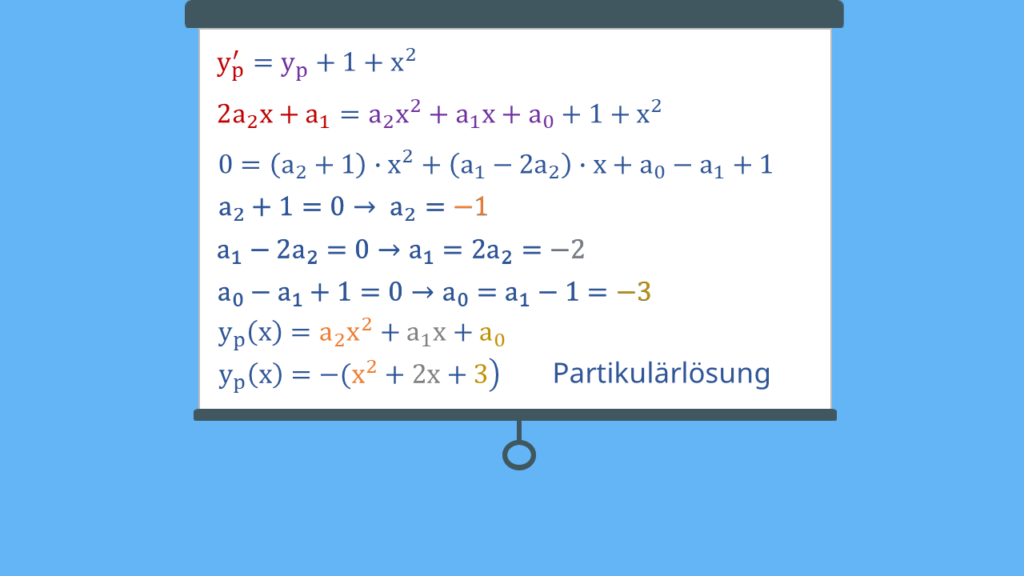
also ein Polynom zweiten Grades, wählen. Darin muss auch der lineare Anteil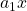 
vorkommen, obwohl es in 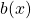keinen linearen Anteil gibt. Nun leitest du den gewählten Ansatz ab.
Beides setzt du dann in die inhomogene DGL ein. Dann sortierst du und vergleichst die Koeffizienten. Daraus resultieren für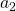 
der Wert -1, für 
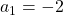und für 
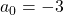. Jetzt kannst du die Koeffizienten in deinen ursprünglichen Ansatz einsetzen. Dann erhältst du die Partikulärlösung. Die Gesamtlösung ist die Summe aus homogener und partikulärer Lösung:
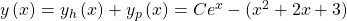
Es ergibt sich hier das gleiche Ergebnis, das man auch mithilfe der Variation der Konstanten erhalten hätte.
Beispiel 2
Nehmen wir mal ein anderes Beispiel:
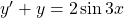
Die homogene Lösung ist leicht zu bestimmen. Es ist:
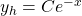
Um jetzt einen Ansatz für die Partikulärlösung zu finden, schaust du dir die Störfunktion an.
An dieser Stelle machen viele Studenten den Fehler, den Ansatz zu wählen, aber dabei den Kosinusanteil zu vergessen. Der Kosinus muss im Ansatz auftauchen, obwohl dieser nicht in der Störfunktion vorkommt. Nur so ist ein trigonometrischer Ansatz vollständig. Jetzt bestimmst du die Ableitung. Wie vorher setzt du danach Ansatz und Ableitung in die DGL ein.
Nachdem wir sortiert haben, können wir mit Koeffizientenvergleich die Konstanten bestimmen. Wir erhalten ein lineares Gleichungssystem. Du kannst zum Beispiel die zweite Gleichung nach A auflösen und sie in die Erste einsetzen. Danach musst du noch nach B umstellen und erhältst als Ergebnis für B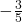 
. Anschließend setzt du B in die zweite Gleichung ein, um A zu bestimmen. A ist 
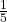. Deine Partikulärlösung ist somit:
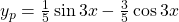
Ausnahmefall: kein zielführender Ansatz
An dieser Stelle noch ein Hinweis: Es ist möglich, dass dein Ansatz nicht zielführend ist. Dann liegt höchstwahrscheinlich ein Resonanzfall vor. Wir zeigen dir mal an folgendem Beispiel, was dann passiert:
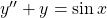
Wir wählen den Ansatz
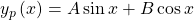
Diesen leiten wir zweimal ab.
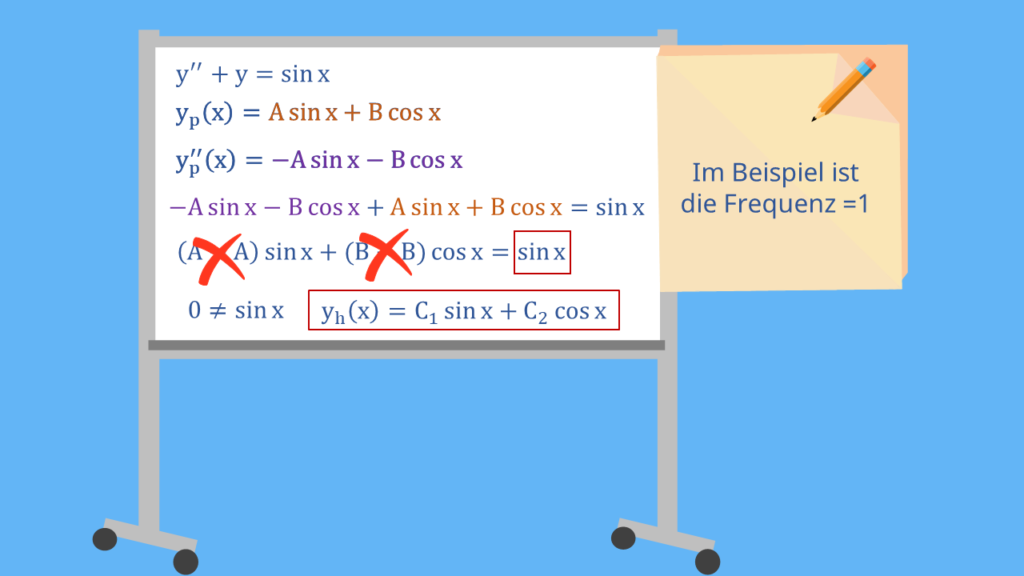
Jetzt setzen wir den Ansatz und die zweite Ableitung in die DGL ein. Danach sortieren wir wieder. A minus A und B minus B fallen raus. Der Ansatz scheitert. Das liegt daran, dass die Störfunktion die gleiche Frequenz, also den gleichen Vorfaktor im Argument des Sinus hat, wie die homogene Lösung.
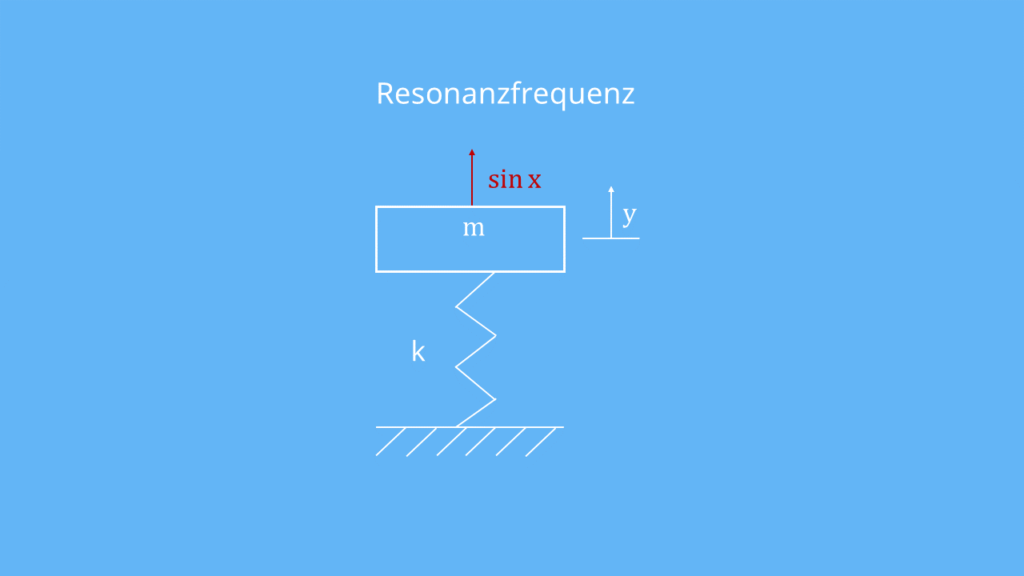
Im Beispiel ist das die Frequenz Eins. Auf eine Schwingung in der Mechanik bezogen heißt das, dass die Anregung die gleiche Frequenz, wie die Eigenschwingung des Systems hat. Das ist die sogenannte Resonanzfrequenz. Eine Anregung in der Resonanzfrequenz, also mit Sinus x, führt dazu, dass sich das System aufschaukelt. Das können die beschränkten Sinus- und Kosinusfunktionen nicht abbilden. Wenn du allerdings mit
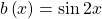
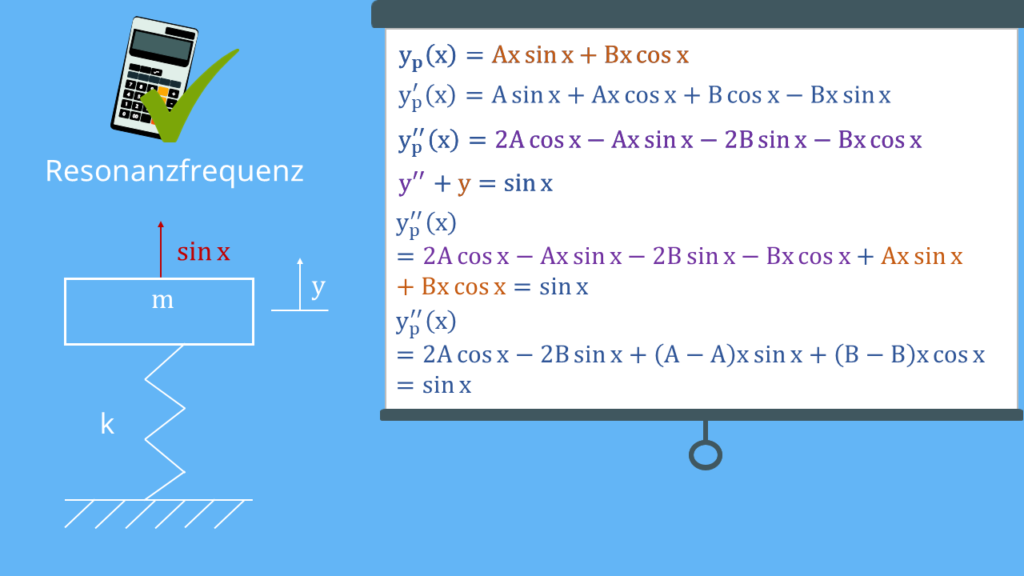
anregst, bleibt die Systemantwort beschränkt. Mit dieser Anregung wäre der gewählte Ansatz nicht gescheitert. Aber du kannst natürlich auch im Resonanzfall die Differentialgleichung lösen. Du musst deinen Ansatz mit x multiplizieren:
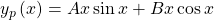
Probier doch mal alleine, die Partikulärlösung zu bestimmen. Die Ableitungen sind diese:
Du bestimmst zunächst wieder die beiden Ableitungen. Danach setzt du alles wieder in die DGL ein. Dieses Ergebnis fasst du dann wieder zusammen und vergleichst die Koeffizienten. Du erhältst für A null und für B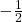 
. Daraus resultiert dann folgendes Endergebnis:
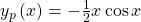
Zusammenfassung der Vorgehensweise
Wiederholen wir noch einmal alles, was wir über den Ansatz der Störfunktion gelernt haben. Die Voraussetzungen sind Folgende. Dir liegt eine lineare Differentialgleichung mit konstanten Koeffizienten vor und deine rechte Seite besteht aus Potenzen, Exponential-, Sinus- oder Kosinusfunktionen oder deren Kombinationen. Mit dem Koeffizientenvergleich bestimmst du die Konstanten. Im Resonanzfall musst du deinen Ansatz mit x multiplizieren.
Ab jetzt hast du immer den Ansatz vom Typ der Störfunktion im Hinterkopf und kannst damit Partikulärlösungen ganz ohne Integrale bestimmen.