Video

Quiz

Variation der Konstanten

Du möchtest wissen, wie die Variation der Konstanten funktioniert? Hier zeigen wird dir, wie man inhomogene Differentialgleichungen mit dieser Methode lösen kann, an einem einfachen Beispiel.

Inhaltsübersicht

Lösung inhomogener, linearer Differentialgleichungen 1. Ordnung

In der Regel sind Differentialgleichungen nicht homogen, sondern inhomogen. Das heißt:

Variation der Konstanten — Homogene Differentialgleichung

Wenn du solch eine inhomogene Differentialgleichung vor dir hast, bestimmst du die Lösung in zwei Schritten: Du berechnest die homogene Lösung 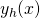y_h(x) und die Partikulärlösung 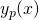y_p(x) . Zusammen ergeben sie die Gesamtlösung.

$y\left(x\right)=y_h\left(x\right)+y_p\left(x\right)$

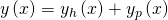
Gängige Methoden zur Bestimmung der Partikulärlösung sind die Variation der Konstanten, die wir hier betrachten oder auch der Ansatz vom Typ der rechten Seite. Wichtig bei der Variation der Konstanten ist, dass deine DGL linear und inhomogen ist.

$y^\prime\left(x\right)+a\left(x\right)y\left(x\right)=b(x)$

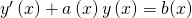
Bestimmung der homogenen Lösung und der Gesamtlösung

Zunächst lösen wir die homogene Gleichung:

$y_h^\prime\left(x\right)+a\left(x\right)y_h\left(x\right)=0$

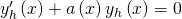
Diese erhältst du, indem du die Inhomogenität einfach weglässt. Die DGL ist trennbar und kann daher mit Trennung der Variablen gelöst werden. Zum Finden der Gesamtlösung benutzen wir diesen Ansatz:

$y\left(x\right)=c\left(x\right)y_h(x)$

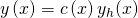
Im homogenen Fall wäre 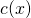c(x) eine Konstante. Da aber von 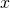abhängt, heißt diese Methode Variation der Konstanten. Die Ableitung ergibt sich mit der Produktregel. Jetzt setzen wir den Ansatz und seine Ableitung in die Differentialgleichung ein.

Variation der Konstanten: Gesamtlösung — Gesamtlösung

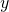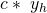Du ersetzt im letzten Term mit $c\ast\ y_h$ . Jetzt kannst du aus den letzten beiden Termen 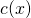c(x) ausklammern. Guck dir den Ausdruck in Klammern an. Es ist genau die homogene DGL. Da sie homogen ist, ist sie bekanntlich gleich Null und kann weggelassen werden. Mit dem gewählten Ansatz gilt also immer:

$b\left(x\right)=c^\prime\left(x\right)y_h(x)$

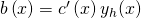
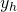y_h hast du bereits bestimmt und 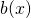b(x) ist gegeben. Umformen nach 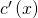$c^\prime\left(x\right)$ und Integrieren nach 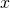führt dich zu einer Lösung für c(x) :

Variation der Konstanten: Ergebnis Partikulärlösung und homogene Lösung — Ergebnis Partikulärlösung und homogene Lösung

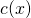Wenn du 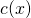c(x) bestimmt hast, erhält du deine Gesamtlösung für 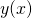y(x) . Viele machen hier den Fehler noch einmal 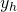y_h zu addieren. Das ist nicht notwendig, da es schon automatisch über die Integrationskonstante C in 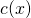c(x) geschieht.

Variation der Konstanten: Beispiel

Jetzt folgt ein Beispiel, um die Variation der Konstanten zu üben:

$y^\prime=y+1+x^2$

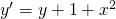
Die homogene Lösung von

$y_h^\prime=y_h$

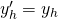
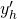$y_h^\prime$ ist gleich 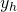y_h ist die e-Funktion mal einer Konstanten C

y_h(x)=Ce^x

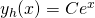
Der Ansatz für die Lösung mit Variation der Konstanten lautet:

$\ y(x)=c(x)e^x$

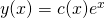
Diesen erhältst du, indem du einfach die Konstante C durch eine Funktion 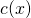c(x) ersetzt. Jetzt nutzen wir die soeben hergeleitete Formel um 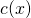c(x) zu bestimmen.

Variation der Konstanten Beispiel — Beispiel

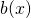Für b(x) setzt du das Polynom 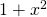1+x^2 ein, das du aus der Differentialgleichung abliest, und für 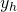y_h die e-Funktion. Jetzt integrieren wir den sich ergebenden Ausdruck. Auf die Integration wollen wir an dieser Stelle nicht genauer eingehen. Als letztes setzt du das 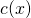c(x) in den Ansatz ein.

Variation der Konstanten Beispiel — Beispiel

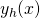y_h(x) ist die e-Funktion, die du auch einsetzen kannst. Jetzt noch ausmultiplizieren und es ergibt sich -(x^2+2x+3)+C_2e^x .

Quiz zum Thema Variation der Konstanten

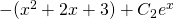Zusammenfassung der Vorgehensweise

Fassen wir zum Schluss zusammen, wie du bei der Variation der Konstanten vorgehst. Erst prüfst du, ob deine DGL linear ist, indem du sie mit dieser Form vergleichst:

$y^\prime\left(x\right)+a\left(x\right)y\left(x\right)=b(x)$

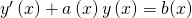
Dann bestimmst du die homogene Lösung 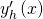$y_h^\prime\left(x\right)$ zur homogenen DGL.

$y_h^\prime\left(x\right)+a\left(x\right)y_h\left(x\right)=0$

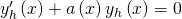
Zum Schluss bestimmst du mit dem Ansatz

$y\left(x\right)=c\left(x\right)y_h(x)$

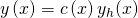
die Gesamtlösung. Du hast eine Lösungstechnik gelernt, mit der du Inhomogenitäten in linearen Differentialgleichungen lösen kannst.

zur Videoseite: Variation der Konstanten

Beliebte Inhalte aus dem Bereich Höhere Analysis

Intro Gewöhnliche Differentialgleichungen lösen

Trennung der Variablen

Variation der Konstanten

Ansatz vom Typ der rechten Seite / Störfunktion

Transformation in System 1. Ordnung

Fundamentalsystem - Wronski-Determinante

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .