Fundamentalsystem und Wronski-Determinante
Du möchtest wissen, was ein Fundamentalsystem ist? Im Folgenden erklären wir dir genauer, was es mit der Fundamentalmatrix und der Wronski-Determinante auf sich hat.
Inhaltsübersicht
Fundamentalsystem, Fundamentalmatrix und Wronski-Determinante Definitionen
Sind die Vektoren 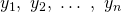 Lösungen der homogenen Differentialgleichung, dann ist auch jede Linearkombination der Lösungen eine Lösung des Differentialgleichungs-Systems.
Lösungen der homogenen Differentialgleichung, dann ist auch jede Linearkombination der Lösungen eine Lösung des Differentialgleichungs-Systems.
Ein System von Lösungsvektoren  heißt linear unabhängig, wenn
heißt linear unabhängig, wenn
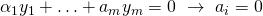
nur die triviale Lösung, also wenn alle Koeffizienten 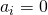 sind, die dargestellte Gleichung löst.
sind, die dargestellte Gleichung löst.
Ein linear unabhängiges System  heißt Fundamentalsystem. Die Lösungen
heißt Fundamentalsystem. Die Lösungen 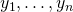 heißen Grundlösungen. Du kannst prüfen, ob ein System linear unabhängig ist, indem du die Determinante der Fundamentalmatrix berechnest. Die Fundamentalmatrix stellst du so auf:
heißen Grundlösungen. Du kannst prüfen, ob ein System linear unabhängig ist, indem du die Determinante der Fundamentalmatrix berechnest. Die Fundamentalmatrix stellst du so auf:
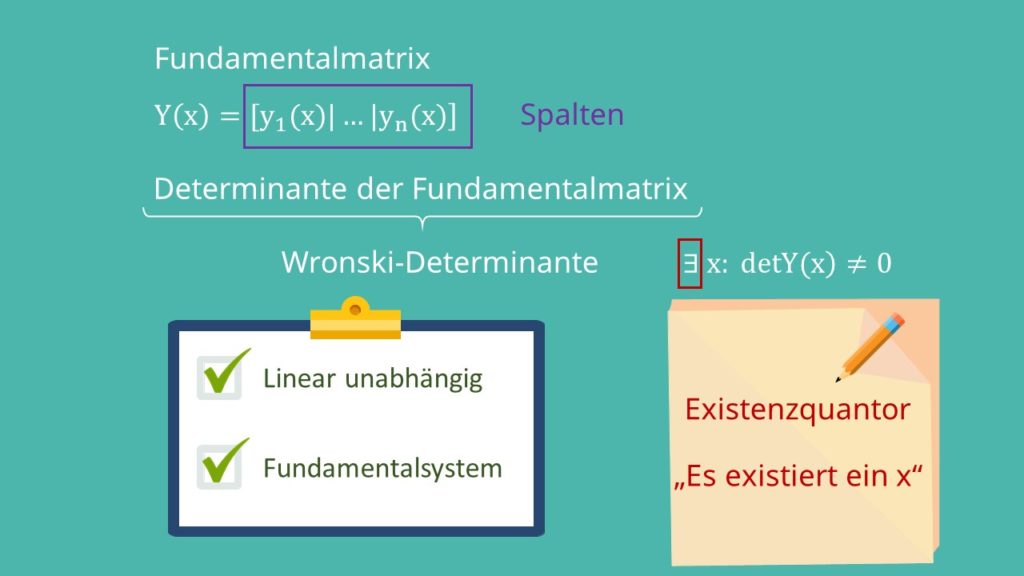
![Rendered by QuickLaTeX.com Y\left(x\right)=[y_1(x)|\ldots|y_n(x)]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-7746434741d66fda24100cf23fb9cb60_l3.png)
Die Spalten sind die Lösungsvektoren 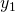 bis
bis 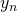 des linearen DGL-Systems erster Ordnung. Die Determinante der Fundamentalmatrix heißt Wronski-Determinante.
des linearen DGL-Systems erster Ordnung. Die Determinante der Fundamentalmatrix heißt Wronski-Determinante.
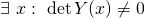
Ist diese für mindestens ein x ungleich Null, sind die Lösungen linear unabhängig und es liegt ein Fundamentalsystem vor. Das umgedrehte E 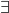 ist der Existenzquantor. Er bedeutet: „Es existiert ein x“
ist der Existenzquantor. Er bedeutet: „Es existiert ein x“
Die allgemeine Lösung ist dann:
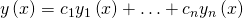
![Rendered by QuickLaTeX.com y\left(x\right)=c_1y_1\left(x\right)+\ldots+c_ny_n\left(x\right)=[y_1(x)|\ldots\left|y_n\left(x\right)\right]\left[\begin{matrix}c_1\\\vdots\ \\c_n\\\end{matrix}\right]=Y\left(x\right)c](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-35ad39cd69b98765c4d103ccb466ed82_l3.png)
Die mit Koeffizienten 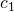 bis
bis 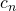 multiplizierten summierten Grundlösungen
multiplizierten summierten Grundlösungen 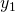 bis
bis 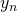 . Du kannst die Lösung auch kompakt in Abhängigkeit von der Fundamental Matrix schreiben.
. Du kannst die Lösung auch kompakt in Abhängigkeit von der Fundamental Matrix schreiben.
Beispiel
Als nächstes schauen wir uns ein Beispiel an.
Dieses System hat dann die Lösungen 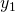 und
und 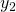 . Dann ergibt sich als Wronski-Determinante:
. Dann ergibt sich als Wronski-Determinante: 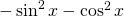 . Das ergibt -1, da
. Das ergibt -1, da 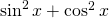 gleich 1 ist.
gleich 1 ist.
-1 ist ungleich Null und damit sind die Lösungen linear unabhängig. Die allgemeine Lösung des DGL-Systems lautet also so:
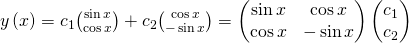
Alternativer Weg zur Bestimmung der Wronski-Determinante
Du kannst die Wronski-Determinante ebenfalls bestimmen, wenn dir ein potentielles Fundamentalsystem 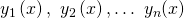 einer skalaren Gleichung n-ter Ordnung vorliegt. Dann kannst du die sogenannte Wronski-Matrix aus den skalaren Lösungen und ihren Ableitungen aufstellen.
einer skalaren Gleichung n-ter Ordnung vorliegt. Dann kannst du die sogenannte Wronski-Matrix aus den skalaren Lösungen und ihren Ableitungen aufstellen.
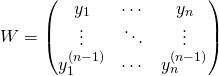
In der obersten Zeile stehen die Funktionen y und in den Zeilen darunter die Ableitungen bis zur n-1ten Ableitung. Das Fundamentalsystem 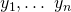 ist genau dann linear unabhängig, wenn
ist genau dann linear unabhängig, wenn
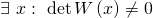
ist.
Zweites Beispiel
Dazu wollen wir uns auch ein Beispiel ansehen. Du hast das Fundamentalsystem 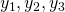 gegeben.
gegeben.
Dann ergibt sich die Wronski-Matrix aus den Ableitungen der drei Lösungen. X abgeleitet ergibt Eins. Noch einmal abgeleitet Null. Die Ableitung von 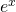 ist
ist 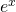 und Sinus abgeleitet ergibt den Kosinus und in der zweiten Ableitung den negativen Sinus. Jetzt musst du die Determinante der Wronski-Matrix bilden.
und Sinus abgeleitet ergibt den Kosinus und in der zweiten Ableitung den negativen Sinus. Jetzt musst du die Determinante der Wronski-Matrix bilden.
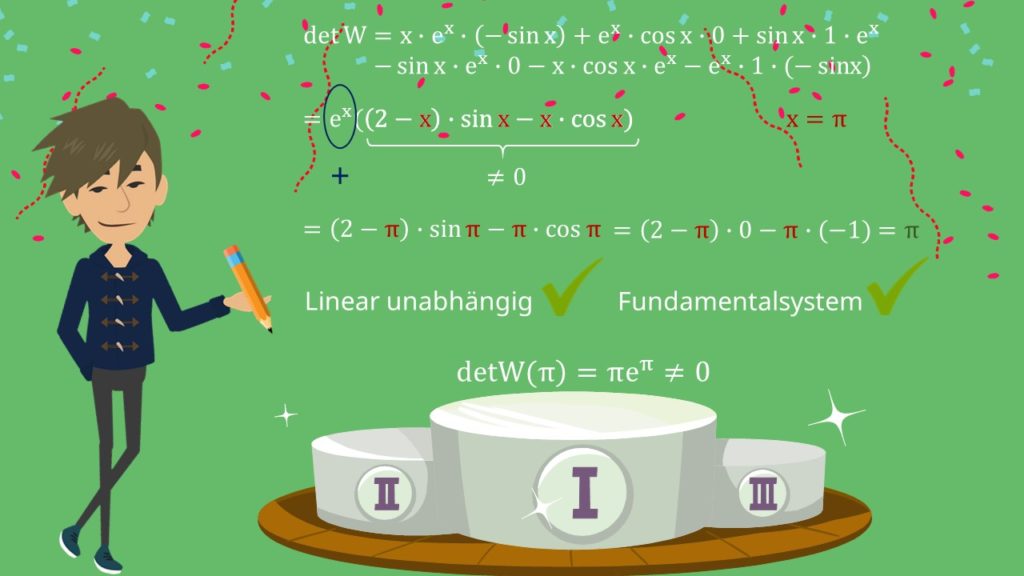
Fassen wir noch schnell zusammen und schauen uns das Ergebnis an. Wir wissen, dass der Faktor 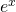 stets positiv ist. Den brauchen wir also nicht weiter zu betrachten.
stets positiv ist. Den brauchen wir also nicht weiter zu betrachten. 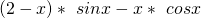 ist im allgemeinen Fall auch nicht gleich Null. Probieren wir das mal für ein beliebiges x aus, zum Beispiel
ist im allgemeinen Fall auch nicht gleich Null. Probieren wir das mal für ein beliebiges x aus, zum Beispiel 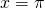 . Wir setzen
. Wir setzen 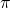 für x ein. Sinus
für x ein. Sinus 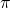 ist gleich Null und Kosinus
ist gleich Null und Kosinus 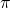 ist gleich -1. Übrig bleibt
ist gleich -1. Übrig bleibt 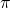 . Also haben wir ein x gefunden, für das die Wronksy-Determinante ungleich Null ist. Die Lösungen sind somit linear unabhängig und es liegt ein Fundamentalsystem vor.
. Also haben wir ein x gefunden, für das die Wronksy-Determinante ungleich Null ist. Die Lösungen sind somit linear unabhängig und es liegt ein Fundamentalsystem vor.
Du hast nun gelernt, was ein Fundamentalsystem, die zugehörige Fundamentalmatrix und die Wronski-Determinante sind.