Binomialmodell
Das Binomialmodell ist eine Methode zur Bewertung von Optionen. Im Anschluss an diese Bewertung lässt sich feststellen, ob die Option fair bewertet wurde. Im folgenden Beitrag erklären wir dir die Vorgehensweise des Binomialmodells genauer.
Einfach erklärt und grafisch aufbereitet bekommst du das Thema in unserem Video . Schau es dir an!
Inhaltsübersicht
Das Binomialmodell – Bewertung von Optionen
Das Binomialmodell (Binomialbaummodell) ist auch unter dem Namen Cox-Ross-Rubinstein-Modell oder CRR-Modell bekannt. Das Vorgehen bei der Bewertung von Optionen mit dem Binomialmodell ist ganz einfach. Wir kennen den Wert der Option nicht, aber dafür die heutigen Werte von Aktien und Zerobonds . Dadurch können wir die Option einfach mit Aktien und Zerobonds nachstellen! Dieses Vorgehen bezeichnet man auch als Duplikationsprinzip.
Die Bedingung ist, dass die Zahlung aus dem Duplikationsportfolio immer der Zahlung des Calls bzw. Puts entspricht. Wir gehen also davon aus, dass wir in diesem Portfolio x Aktien und einen Zerobond haben. Damit können wir unsere Option nachbauen.
Binomialmodell: Beispiel Call
Zuerst beschäftigen wir uns mit einem Call. Dafür legen wir fest, dass unser  , also der Fälligkeitszeitpunkt, nach
, also der Fälligkeitszeitpunkt, nach  Jahren ist. Nach
Jahren ist. Nach  Jahren sollte also die Zahlung aus unserem Duplikationsportfolio genauso viel wert sein, wie eine Option, deren Wertänderungsfaktor zum Beispiel nach oben
Jahren sollte also die Zahlung aus unserem Duplikationsportfolio genauso viel wert sein, wie eine Option, deren Wertänderungsfaktor zum Beispiel nach oben  und nach unten
und nach unten  beträgt. Kurz gesagt:
beträgt. Kurz gesagt:  ist unser up und
ist unser up und  ist unser down. Das heißt, bei einem aktuellen Kurswert der Aktie von
ist unser down. Das heißt, bei einem aktuellen Kurswert der Aktie von  haben wir nach
haben wir nach  Jahren entweder einen Aktienkurs von
Jahren entweder einen Aktienkurs von  oder
oder  .
.
Gehen wir in unserem Beispiel von einem Basispreis in Höhe von  aus. Jetzt wissen wir auch, wie viel Gewinn wir machen würden. Wir nehmen dafür immer den maximalen Wert zwischen Endwert der Aktie abzüglich Basispreis und null. Das heißt also wir erhalten als Gewinn für beide Möglichkeiten die Werte
aus. Jetzt wissen wir auch, wie viel Gewinn wir machen würden. Wir nehmen dafür immer den maximalen Wert zwischen Endwert der Aktie abzüglich Basispreis und null. Das heißt also wir erhalten als Gewinn für beide Möglichkeiten die Werte  und
und  .
.
Daraus können wir nun zwei Gleichungen aufstellen, die jeweils zwei Unbekannte enthalten. Dadurch können wir die Gleichungen nun einfach gleichsetzen und nach  auflösen. Unser
auflösen. Unser  ist in diesem Fall also
ist in diesem Fall also  . Wir brauchen demnach
. Wir brauchen demnach  Aktien zur Duplikation unserer Option.
Aktien zur Duplikation unserer Option.
Jetzt müssen wir nur noch den Zerobond bestimmen. Wähl dazu einfach eine der Anfangsgleichungen aus. Wir nehmen hier die zweite, weil sie einfacher ist. Jetzt setzen wir unser  ein und erhalten somit für unseren Zerobond in
ein und erhalten somit für unseren Zerobond in  Jahren den Wert
Jahren den Wert  . Wir brauchen aber den Wert des Zerobonds heute, deshalb zinsen wir ab! Ist der Marktzinssatz also zum Beispiel zehn Prozent, wäre unser Zerobond gleich
. Wir brauchen aber den Wert des Zerobonds heute, deshalb zinsen wir ab! Ist der Marktzinssatz also zum Beispiel zehn Prozent, wäre unser Zerobond gleich  .
.
Somit haben wir alle Summanden und können nun den fairen Preis der Call-Option bestimmen. Wir erhalten 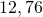 . Wir sind also long in Aktien und short in Zerobonds.
. Wir sind also long in Aktien und short in Zerobonds.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Binomialmodell: Beispiel Put
Bei einem Put ist es genau umgekehrt. Dort sollte unser Besitz an Aktien immer negativ sein, dafür der Besitz an Zerobonds immer positiv – also short in Aktien und long in Zerobonds. Vergiss aber nicht: Bei der Payoffberechnung eines Puts musst du im Gegenteil zum Call das Maximum zwischen Basispreis abzüglich Endwert und null wählen.
Du siehst, dass eine präferenzfreie Bewertung möglich ist! Das heißt, wir müssen nicht die Eintrittswahrscheinlichkeiten der beiden möglichen Werte oder gar die Risikoeinstellung des Anlegers kennen.
Einflüsse auf den Optionspreis
Welche Werte haben dann stattdessen einen Einfluss auf den Optionspreis? Wichtig für die Berechnung sind auf jeden Fall der Kurswert der Aktie in  , also
, also  , der Basispreis der Option
, der Basispreis der Option  , der Geldmarktzinssatz, die Laufzeit der Option sowie die Wertänderungsfaktoren für up und down.
, der Geldmarktzinssatz, die Laufzeit der Option sowie die Wertänderungsfaktoren für up und down.
Klar, wenn die Aktienkurse oder die Basispreise sich verändern, verändert sich auch die Ausgangssituation unseres Calls oder Puts. Was vielleicht nicht direkt auf den ersten Blick ersichtlich ist: Optionen sind auch von der Volatilität, dem Zinssatz und der Laufzeit beeinflussbar! Die Volatilität führt zu größeren Gewinnmöglichkeiten. Zinssätze beeinflussen dagegen die Zerobondwerte. Nehmen wir an, sie steigen. Dann sinken die Zerobondskurse. Da wir im Call short und im Put long in Zerobonds sind, steigt unser Call, wenn Zerobondpreise sinken, während der Put fällt.
Wenn sich nun die Laufzeit verändert, sind die Entwicklungen nicht ganz klar. Denn mit einer höheren Laufzeit steigt zwar die Gesamtvolatilität, dafür sinken aber die Zerobondpreise. Somit wissen wir: Bei einem Call steigt auf jeden Fall der Wert! Aber bei einem Put ist das nicht ersichtlich, denn die steigende Gesamtvolatilität wirkt sich positiv darauf aus, aber der sinkende Zerobondpreis beeinflusst wiederum negativ.





