Value at Risk
Der Value at Risk oder kurz VaR, ist ein zentrales Risikomaß zur Bestimmung des höchsten zu erwartenden Verlustes. Im Folgenden erklären wir die Definition, die Formel und gehen auf die Berechnung mit einem Beispiel.
Du willst das Thema auf Anhieb gut verstehen? Dann schau dir unser Video an! Denn hier haben wir alles Schritt für Schritt erklärt.
Inhaltsübersicht
Value at Risk einfach erklärt
Value at Risk (oder auch VaR) ist ein strategisches Modell, mit dem man Risiken auf finanziellen Märkten, also Marktpreisrisiken messen kann.
Der Value at Risk beschreibt den maximal zu erwartenden Wertverlust eines Portfolios, der mit der Wahrscheinlichkeit  innerhalb einer Halteperiode, unter den üblichen Marktbedingungen nicht überschritten wird.
innerhalb einer Halteperiode, unter den üblichen Marktbedingungen nicht überschritten wird.
Es existieren allerdings verschiedene Risikoarten. Das Risiko, das für Investitionen besonders relevant ist, ist das Marktpreisrisiko. Dieses bezeichnet das Risiko eines Verlustes, der sich ergeben kann, weil sich die Marktpreise verändern. Es ist auch unter dem Begriff Marktrisiko bekannt.
Konfidenzniveau bestimmen
Um den Value at Risk berechnen zu können, müssen wir uns noch kurz mit dem Konfidenzniveau beschäftigen.  ist das spezifizierte Konfidenzniveau, das in der Regel zwischen
ist das spezifizierte Konfidenzniveau, das in der Regel zwischen  und
und  liegt. Das Konfidenzniveau besagt, mit welcher Wahrscheinlichkeit unser berechneter Wert zutreffend ist. Das heißt also, wenn wir ein
liegt. Das Konfidenzniveau besagt, mit welcher Wahrscheinlichkeit unser berechneter Wert zutreffend ist. Das heißt also, wenn wir ein  von
von  haben, beträgt unser spezifiziertes Konfidenzniveau
haben, beträgt unser spezifiziertes Konfidenzniveau  . Unser Value at Risk wird also in diesem Fall mit der Wahrscheinlichkeit von
. Unser Value at Risk wird also in diesem Fall mit der Wahrscheinlichkeit von  in unserer Halteperiode nicht überschritten. Was ist eine Halteperiode, fragst du dich jetzt? Das ist einfach nur der festgelegte Zeitraum, für den wir unseren VaR berechnen.
in unserer Halteperiode nicht überschritten. Was ist eine Halteperiode, fragst du dich jetzt? Das ist einfach nur der festgelegte Zeitraum, für den wir unseren VaR berechnen.
Meistens kaufen Anleger, die viel investieren, heutzutage Portfolios. Denn wenn man mehrere Aktien zusammenlegt, die nicht vollständig positiv korreliert sind, kann sich dadurch das Gesamtrisiko reduzieren! Das nennt man auch Diversifikation. Schauen wir uns die Value at Risk Berechnung also am Beispiel eines Portfolios an.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Value at Risk berechnen
Angenommen du besitzt folgendes Portfolio:
- Der Marktwert
 beträgt
beträgt 
- Das Konfidenzniveau ist

- Die Halteperiode entspricht einem Tag.
- Das Portfolio besteht aus drei Aktien.
- Die Renditen sind multivariate Normalverteilt – das heißt, alle Aktien sind normalverteilt, haben also einen Erwartungswert und man kann ihre Varianz berechnen.
-
 der Erwartungswert des Portfolios ist
der Erwartungswert des Portfolios ist - Die Standardabweichung
 beträgt.
beträgt.
Was ist der Value at Risk? Um diesen zu berechnen brauchen wir zuerst die Formel dazu.
Value at Risk Formel
Die Formel für den Value at Risk lautet:

Dabei steht
-
 steht für das
steht für das  -Quantil der Standardnormalverteilung,
-Quantil der Standardnormalverteilung, -
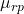 für den Erwartungswert unserer Portfoliorenditen,
für den Erwartungswert unserer Portfoliorenditen, -
 für die Standardabweichung unserer Portfoliorenditen.
für die Standardabweichung unserer Portfoliorenditen.
Du hast bestimmt schon einmal die Dichtefunktion der Normalverteilung gesehen. Wenn nicht bewusst, dann bestimmt unbewusst, denn sie ist auch unter dem Namen Gaußkurve bekannt und unter anderem auf dem alten Zehn-Markschein zu sehen. Was wir hier berechnen, ist quasi die Fläche unter der Kurve, die genau  beträgt. Wir sehen, bei welchem Wert die Abgrenzungslinie der Fläche die x-Achse schneidet. Das ist dann unser Value at Risk.
beträgt. Wir sehen, bei welchem Wert die Abgrenzungslinie der Fläche die x-Achse schneidet. Das ist dann unser Value at Risk.
Value at Risk berechnen Schritt für Schritt
Zur Vereinfachung nehmen wir in unserem Beispiel an, dass  ist und
ist und  . Am häufigsten wird mit einem Alpha von
. Am häufigsten wird mit einem Alpha von  oder
oder  , also einem Konfidenzniveau von
, also einem Konfidenzniveau von  oder
oder  gerechnet. Um die
gerechnet. Um die  -Quantile der Standardnormalverteilung zu erhalten, gehst du nun folgendermaßen vor: Zuerst nimmst du die Verteilungstabelle der Standardnormalverteilung zu Hilfe.
-Quantile der Standardnormalverteilung zu erhalten, gehst du nun folgendermaßen vor: Zuerst nimmst du die Verteilungstabelle der Standardnormalverteilung zu Hilfe.
Dort suchst du einfach nach dem gewünschten Konfidenzniveau, in unserem Fall die  , also den Wert
, also den Wert  . In den meisten Fällen wirst du das Konfidenzniveau nicht genau finden. Daher suchst du einfach die beiden Werte, die deinem Konfidenzniveau am nächsten sind und nimmst dann den Mittelwert der beiden. In unserem Beispiel wären das die Werte
. In den meisten Fällen wirst du das Konfidenzniveau nicht genau finden. Daher suchst du einfach die beiden Werte, die deinem Konfidenzniveau am nächsten sind und nimmst dann den Mittelwert der beiden. In unserem Beispiel wären das die Werte  und
und  , also ein
, also ein  in Höhe von
in Höhe von  und
und 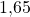 . Damit erhalten wir für die
. Damit erhalten wir für die  -Quantile:
-Quantile:  und
und  .
.
Der letzte Schritt ist simpel. Wir setzen nun alles in die Value at Risk Formel ein und erhalten als Ergebnis für die Value at Risk Berechnung  .
.
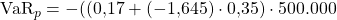
Das heißt folglich: Mit einer Wahrscheinlichkeit von  überschreitet der Verlust unseres Portfolios nicht mehr als
überschreitet der Verlust unseres Portfolios nicht mehr als  bis zum nächsten Tag.
bis zum nächsten Tag.
Geschafft! Jetzt weißt du bestens Bescheid über den Value at Risk Bescheid und kannst ihn für dein nächstes Portfolio ganz einfach selbst berechnen.




