Video

Quiz

Charakteristisches Polynom

Wichtige Inhalte in diesem Video

Herleitung charakteristisches Polynom

Beispiel 1: Charakteristisches Polynom berechnen

Weiteres Beispiel: charakteristisches Polynom berechnen

Charakteristisches Polynom Matrix

Du möchtest wissen, was ein charakteristisches Polynom ist? Hier zeigen wir dir, wie du lineare Differenzialgleichungen mit konstanten Koeffizienten mithilfe des charakteristischen Polynoms lösen kannst.

Inhaltsübersicht

Herleitung charakteristisches Polynom

im Videozur Stelle im Video springen

Eine homogene Differenzialgleichung n-ter Ordnung mit konstanten Koeffizienten sieht so aus.

$a_ny^{\left(n\right)}+a_{n-1}y^{(n-1)}+\ldots+a_1y^\prime+a_0y=0$

Jetzt wollen wir das charakteristische Polynom herleiten. Dazu wählen wir einen Exponentialansatz für y,

$y\left(x\right)=e^{\lambda x}$

und zwar $e^{\lambdax}$ . Diesen kannst du beliebig oft ableiten.

Charakteristisches Polynom — Herleitung charakteristisches Polynom

Danach setzt du den Ansatz und seine Ableitungen in die DGL ein. $e^{\lambdax}$ kommt in jedem Summanden vor. Also kannst du es ausklammern. Das Produkt ist Null, wenn entweder $e^{\lambdax}$ oder der Ausdruck in Klammern Null ist. Natürlich weißt du, dass $e^{\lambdax}$ niemals Null wird. Folglich muss der Ausdruck in Klammern gleich Null sein, damit die Gleichung erfüllt ist.

$a_n\lambda^n+a_{n-1}\lambda^{n-1}+\ldots+a_1\lambda+a_0=0$

Diese nennt sich charakteristisches Polynom oder charakteristische Gleichung, von der du die Nullstellen $\lambda_i$ berechnest. Anschließend setzt du diese in den Exponentialansatz ein und erhältst das Fundamentalsystem deiner Differenzialgleichung.

Beispiel 1: Charakteristisches Polynom berechnen

im Videozur Stelle im Video springen

Jetzt wollen wir uns das Ganze an einem Beispiel einmal genauer anschauen:

$y^{\left(3\right)}-6y^{\prime\prime}+11y^\prime-6y=0$

Du kennst jetzt die Herleitung über den Exponentialansatz, du kannst aber Zeit sparen, wenn du das charakteristische Polynom direkt aus der Differenzialgleichung abliest.

$\lambda^3-6\lambda^2+11\lambda-6=0$

Charakteristisches Polynom berechnen — Beispiel 1

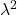Für die dritte Ableitung schreibst du dann $\lambda^3$ , für die zweite $\lambda^2$ und für die erste $\lambda$ . Die Funktion selbst verschwindet einfach, sodass der Faktor 6 alleine dasteht. Jetzt wollen wir die Nullstellen des entstandenen charakteristischen Polynoms bestimmen. Wie das geht, solltest du bereits von Eigenwertaufgaben kennen. Du rätst die erste Lösung $\lambda_1=1$ . Setzt du sie ein, stellst du fest, dass 1 die Gleichung erfüllt.

Als Nächstes machst du eine Polynomdivision. Übrig bleibt ein Polynom zweiten Grades, das du mit der pq-Formel lösen kannst. Du erhältst $\lambda_2$ gleich 2 und $\lambda_3$ gleich 3. Unsere geratene Lösung war $\lambda_1$ gleich 1. Eingesetzt in den Exponentialansatz ergibt sich das Fundamentalsystem

$\left\{e^x,e^{2x},e^{3x}\right\}$

Beispiel 2

im Videozur Stelle im Video springen

Machen wir noch ein zweites Beispiel.

$y^{\prime\prime}+4y^\prime+4=0$

Charakteristisches Polynom berechnen — Beispiel 2

Das charakteristische Polynom ergibt sich dann wieder direkt aus der Differenzialgleichung. Somit kannst du es mit der pq-Formel lösen. An der Stelle -2 tritt eine doppelte Nullstelle auf. Das würde auf zweimal ein und dieselbe Lösung führen. Wir wollen aber zwei linear unabhängige Lösungen bestimmen. Um eine zweite Lösung zu erhalten, multiplizieren wir die Lösung mit x und erhalten das Fundamentalsystem.

Weiteres Beispiel: charakteristisches Polynom berechnen

im Videozur Stelle im Video springen

Wir gehen weiter zum nächsten Beispiel.

$y^{\prime\prime}-2y^\prime+2y=0$

Wie du das charakteristische Polynom bestimmst und löst, weißt du bereits.

Charakteristisches Polynom berechnen — Beispiel 3

Doch diesmal ergeben sich für Lambda komplexe Zahlen. Du willst allerdings ein rein reelles Fundamentalsystem bestimmen. Auch das kriegst du hin. Zunächst stellst du das komplexe Fundamentalsystem auf. Jetzt wendest du die Euler‘sche Formel an.

Diese kannst du dir jederzeit aus der Zeigerdarstellung einer komplexen Zahl in der komplexen Ebene herleiten. x ist der Winkel und du kannst die komplexe Zahl entweder als 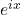$e^{ix}$ schreiben oder in seine Anteile in der komplexen Ebene aufteilen. Der Kosinus gibt den Realteil an und der Sinus des Winkels den Imaginärteil.

Reelles Fundamentalsystem

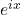Kommen wir zurück zu unserem Fundamentalsystem. $e^{(1+i)x}$ kannst du als Produkt angeben. Nun schreiben wir das $e^{ix}$ mit der Euler’schen Formel um. Dasselbe machen wir für y_2 . Außer einem Minus erhalten wir dasselbe Ergebnis.

Rein reell sind diese Fundamentalsysteme aber dadurch immer noch nicht. Aber du kannst geschickt Linearkombinationen bilden, sodass die Imaginärteile sich gegenseitig aufheben. Addiere die beiden Lösungen und multipliziere die Summe mit $\frac{1}{2}$ . Das Ergebnis nennen wir ${\widetilde{y}}_1$ . Das $i\ \sin{x}$ aus y_1 und das $-\ \sin{x}$ heben sich auf und es bleibt die rein reelle Lösung $e^x\cos{x}$ . Das Gleiche machen wir für ${\widetilde{y}}_2$ . Dafür nimmst du $y_1\ -2\ast\frac{i}{2}$ . Wieder ergibt sich eine reelle Lösung: $e^x\sin{x}$ .

Quiz zum Thema Charakteristisches Polynom

Charakteristisches Polynom Matrix

im Videozur Stelle im Video springen

Auch bei Systemen hilft dir das charakteristische Polynom.

$y^\prime=\left(\begin{matrix}0&1\\-2&3\\\end{matrix}\right)y$

Da y hier ein Vektor ist, suchst du Lösungen in Vektorform und bestimmst dafür die Eigenwerte und Eigenvektoren der Matrix A.

Charakteristisches Polynom in Systemen

Auch hier erhältst du dann nach der Bestimmung der Determinanten ein charakteristisches Polynom. Es ist $\lambda^2-3\lambda+2$ . Die Eigenwerte sind $\lambda_1=1$ und $\lambda_2=2$ . Als Nächstes bestimmst du die Eigenvektoren:

$\left(A-\lambda_iE\right)v_i=0$

Dafür musst du die einzelnen $\lambda_i$ in $\left(A-\lambda_iE\right)$ einsetzen. Mit scharfem Hinsehen erkennst du den Eigenvektor 1 1. Als Nächstes schaust du dir die Gleichung für $\lambda_2$ an. Der sich ergebene Eigenvektor ist 1 2. Somit erhältst du diese beiden Lösungen, wenn du die Eigenwerte und die zugehörigen Eigenvektoren einsetzt. Sie bilden ein Fundamentalsystem.

Charakteristisches Polynom — Fundamentalsystem

Du hast somit gelernt, wie du mithilfe des Exponentialansatzes und des charakteristischen Polynoms Differenzialgleichungen löst. Außerdem weißt du mit doppelten Nullstellen umzugehen und kannst für komplexe Nullstellen ein reelles Fundamentalsystem bestimmen. Zudem hast du den Exponentialansatz für Systeme kennengelernt.

zur Videoseite: Charakteristisches Polynom

Beliebte Inhalte aus dem Bereich Höhere Analysis

Intro Differentialgleichung - Grundbegriffe

Differentialgleichung

Gewöhnliche DGL

DGL 1. & 2. & höherer Ordnung

Homogene & inhomogene DGL

Lineare & nichtlineare DGL

Charakteristisches Polynom

Anfangswertproblem

Randwertproblem

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .