Video anzeigen

pq Formel

Wichtige Inhalte in diesem Video

Quadratische Gleichungen mittels pq-Formel berechnen

Wenn du wissen willst, wie die pq Formel aussieht und wozu du sie benötigst, bist du in diesem Artikel genau richtig. Du lernst leichter, wenn du Schritt für Schritt sehen kannst, wie du die pq-Formel anwendest? Dann schau dir am besten unser Video an.

Inhaltsübersicht

pq Formel einfach erklärt

Du möchtest eine quadratische Gleichung lösen, die so aussieht?

x²+ 2x -3 =0

Dafür brauchst du die pq-Formel :

pq Formel

$\mathbf{x_{1,2} = -\cfrac{\textcolor{red}{p}}{2} \pm \sqrt{\left(\frac{\textcolor{red}{p}}{2}\right) ^2-\textcolor{blue}{q}}}$

In die pq Formel kannst du dann einfach die Zahlen aus deiner Gleichung einsetzen. Dabei nimmst du für p die Zahl, die vor dem einzelnen x steht und für q die Zahl ohne x:

$x_{1,2} = -\cfrac{\textcolor{red}{p}}{2} \pm \sqrt{\left(\frac{\textcolor{red}{p}}{2}\right) ^2-\textcolor{blue}{q}}=-\cfrac{\textcolor{red}{2}}{2}\pm\sqrt{\left(\frac{\textcolor{red}{2}}{2}\right)^2-\left(\textcolor{blue}{-3}\right)}$

Wegen dem ± kannst du zwei Lösungen berechnen:

$\begin{align*}x_1&=-\dfrac{2}{2}+\sqrt{\left(\frac{2}{2}\right)^2-\left(-3\right)}=1\\ x_2&=-\dfrac{2}{2}-\sqrt{\left(\frac{2}{2}\right)^2-\left(-3\right)}=-3\end{align*}$

Dir ging das zu schnell? Kein Problem! In unserem Einsteiger-Video haben wir eine leichte Schritt für Schritt Anleitung für dich.

Quadratische Gleichungen mittels pq-Formel berechnen

im Videozur Stelle im Video springen

(00:54)

Willst du die pq-Formel zur Berechnung quadratischer Funktionen anwenden, dann befolgst du am besten die folgende Schritt-für-Schritt-Anleitung.

pq-Formel anwenden — Schritt für Schritt

Bringe die Gleichung in die Normalform x² + px + q = 0.
Lies p und q ab.
Setze p und q in die pq-Formel ein.
Berechne die Lösungen.
Schreibe die Lösungsmenge auf.

Schau dir die Schritte gleich an einem konkreten Beispiel für eine quadratische Gleichung an:

2x²– 4x = 30.

Schritt 1: Forme die Gleichung so um, dass auf einer der beiden Seiten die Null steht. Damit bringst du die quadratische Gleichung in die allgemeine Form. Um die pq Formel anwenden zu können, darf vor dem x² jedoch kein Vorfaktor stehen. Das heißt du teilst die ganze Gleichung durch die Zahl vor dem x², hier die Zahl 2! Somit hast du die Gleichung auf Normalform gebracht

2x²-4x = 30 | -30 :2

x²-2x – 15 = 0

Schritt 2: Lies als nächstes die Koeffizienten p und q ab

p=-2, q=-15.

Schritt 3: Setze p und q in die pq-Formel ein

$x_{1,2} = -\cfrac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right) ^2-q}$

$x_{1,2} = -\cfrac{-2}{2} \pm \sqrt{\left(\frac{-2}{2}\right) ^2-(-15)}$ .

Schritt 4: Berechne die Ergebnisse

$x_{1,2} = -\cfrac{-2}{2} \pm \sqrt{\left(\frac{-2}{2}\right) ^2-(-15)} = 1 \pm \sqrt{1+15}$

$\Longrightarrow$ x₁ = 1 + 4 = 5 und x₂ = 1 – 4 = -3.

Schritt 5: Schreibe die Lösungsmenge auf

$\mathbb{L} = \{-3; 5\}$ .

Diese Anleitung zur Verwendung der pq-Formel kannst du für jede quadratische Gleichung benutzen. Aber woher weißt du, wie viele Lösungen es gibt?

Diskriminante der pq Formel

im Videozur Stelle im Video springen

(01:59)

Der Term $\left(\frac{p}{2}\right) ^2-q$ unter der Wurzel der pq Formel wird Diskriminante genannt. Dabei wird niemand diskriminiert, das Wort kommt lediglich aus dem Lateinischen und bedeutet „unterscheiden“. Die Diskriminante gibt dir Auskunft darüber, ob eine quadratische Gleichung eine, zwei oder keine Lösung hat. Das erkennst du ganz einfach an ihrem Vorzeichen.

Diskriminante der pq-Formel

$D=\left(\frac{p}{2}\right) ^2-q$

$\left(\frac{p}{2}\right)^2-q >0$ : Die quadratische Gleichung hat zwei Lösungen
$\left(\frac{p}{2}\right)^2-q =0$ : Die quadratische Gleichung hat eine Lösung
$\left(\frac{p}{2}\right)^2-q <0$ : Die quadratische Gleichung hat keine Lösung

Berechnest du die Diskriminante einer quadratischen Funktion , so kannst du daran direkt die Anzahl der Nullstellen ablesen.

Nullstellen quadratischer Funktionen, Nullstelle, Parabeln, Parabel Diskriminante pq Formel — Anzahl der Nullstellen und Diskriminante

pq-Formel anwenden

Die pq-Formel ist eine quadratische Lösungsformel. Du kannst sie für alle quadratischen Gleichungen in der Normalform verwenden. Das bedeutet, vor x²darf keine Zahl stehen. Hier siehst du eine Übersicht über die verschiedenen Arten quadratischer Gleichungen:

Reinquadratisch ohne Absolutglied (q = 0, p = 0): x² = 0
Reinquadratisch mit Absolutglied (p = 0): x² + q = 0
Gemischtquadratisch ohne Absolutglied (q = 0): x² + px = 0
Gemischtquadratisch mit Absolutglied: x² + px + q = 0

Tipp: Es lohnt sich vor allem, die pq-Formel für gemischtquadratische Gleichungen mit Absolutglied zu benutzen. Für die anderen Normalformen gibt es leichtere Lösungsverfahren. Mehr dazu findest du auch in unserem Video zu Quadratische Gleichungen lösen .

pq Formel berechnen: ohne p

im Videozur Stelle im Video springen

(03:29)

Ist in der quadratischen Gleichung p = 0, so kannst du das Ergebnis zwar mithilfe der pq Formel berechnen, jedoch bist du vermutlich schneller, wenn du einfach die Wurzel ziehst. Der Term hat dann immer die Form:

x²+ q = 0

Du kannst ihn umformen, indem du nach x² auflöst und dann die Wurzel ziehst:

x^2 = -q

$x_{1,2} = \pm \sqrt{-q}$

Willst du beispielsweise x²– 20,25 = 0 berechnen, so erhältst du als Ergebnis

x^2 = 20,25

$x_{1,2} = \pm \sqrt{20,25} = \pm 4,5$

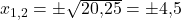
$\Rightarrow x_1 = 4,5$ und x_2=-4,5.

pq Formel berechnen: ohne q

Hast du hingegen einen Term gegeben, bei dem q = 0 ist, so löst du die Funktionsgleichung am besten durch Ausklammern. Dann kannst du die Nullstellen der beiden Faktoren separat bestimmen:

x²+ px=0

x(x + p) = 0

x₁ = 0 und x₂ = -p.

pq-Formel Beispiele

In diesem Abschnitt zeigen wir dir drei verschiedene Beispiele, bei denen die pq-Formel jeweils unterschiedlich viele Lösungen liefert.

Beispiel 1: pq-Formel mit zwei Lösungen

Gegeben sei die quadratische Gleichung

x²=7x+8.

Um sie mithilfe der pq-Formel zu lösen, bringen wir sie zuerst auf Normalform

x²=7x +8 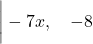$\bigg| -7x, \quad -8$

x²-7x-8=0

Jetzt können wir die Parameter p=-7 und q=-8 bestimmen und sie in die pq-Formel einsetzen

$x_{1,2} = -\cfrac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right) ^2-q}$

$x_{1,2} = -\cfrac{-7}{2} \pm \sqrt{\left(\frac{-7}{2}\right) ^2-(-8)}$ .

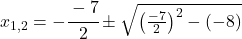Die beiden Lösungen x₁ und x₂kannst du nun ganz einfach ausrechnen

$x_{1,2} = -\cfrac{-7}{2} \pm \sqrt{\left(\frac{-7}{2}\right) ^2-(-8)} = 3,5 \pm \sqrt{\left(3,5\right) ^2+8} = 3,5 \pm \sqrt{20,25}$

$\Longrightarrow$ x₁ =3,5+4,5= 8 und x₂ = 3,5-4,5=-1.

$\Longrightarrow \quad \mathbb{L} = \{-1; 8 \}$ .

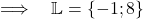Beispiel 2: pq-Formel mit einer Lösung

Die pq-Formel hat genau eine Lösung, wenn die Diskriminante gleich Null ist. Ein Beispiel dafür ist die Gleichung

-2x²-20x-50=0.

Diese Gleichung liegt nicht in der Normalform vor, da x²noch den Vorfaktor -2 besitzt. Daher teilen wir die quadratische Gleichung durch -2 und erhalten so die Normalform

x²+10x+25=0.

Nun können wir p=10 und q = 25 direkt ablesen und in die pq Formel einsetzen

$x_{1,2} = -\cfrac{10}{2} \pm \sqrt{\left(\frac{10}{2}\right) ^2-25} =-5 \pm \sqrt{5^2-25} = -5 \pm 0 = -5$ .

Die Lösungsmenge besteht in diesem Fall nur aus einem Element $\mathbb{L}=\{-5\}$ .

Merke: Solche Gleichungen könntest du auch lösen, indem du die binomischen Formeln anwendest.

x²+10x+25= (x+5)²

Beispiel 3: pq Formel mit keiner Lösung

Als letztes Beispiel betrachten wir noch den Fall, dass die pq Formel keine Lösung liefert. Hier ist die Diskriminante stets kleiner als Null, was dazu führt, dass du eine negative Wurzel erhältst. Dafür betrachten wir

x²+2x+4=0

mit p=2 und q=4. Das Einsetzen der Werte in die pq-Formel ergibt hier

$x_{1,2} = -\cfrac{2}{2} \pm \sqrt{\left(\frac{2}{2}\right) ^2-4} = -1 \pm \sqrt{1^2-4} = -1 \pm \sqrt{-3}.$

Auch hier darfst du die Lösungsmenge nicht vergessen aufzuschreiben, obwohl es sich um die leere Menge handelt

$\mathbb{L}=\emptyset=\{\}.$

pq-Formel — kurz und knapp

Mit der pq-Formel kannst du quadratische Gleichungen lösen. Sie haben allgemein die Form f(x) = y = x² + px + q = 0, also zum Beispiel x² + 2x + 1 = 0 oder x² – 3x + 5 = 0.

pq-Formel Herleitung

Vielleicht fragst du dich, woher die pq Formel eigentlich kommt. Dafür wollen wir eine quadratische Gleichung in Normalform mittels quadratischer Ergänzung nach x auflösen.

x²+px+q=0 $\bigg| -q$

x²+px=-q.

Die linke Seite wollen wir nun quadratisch ergänzen, weswegen wir zuerst den Ausdruck px umschreiben und dann auf beiden Seiten $\left(\frac{p}{2}\right)^2$ addieren

$x^2+2 \frac{p}{2}x = -q$

$x^2+2 \frac{p}{2}x + \left(\frac{p}{2}\right)^2 = \left(\frac{p}{2}\right)^2-q$

Jetzt lässt sich die linke Seite der Gleichung mithilfe der ersten binomischen Formel vereinfachen

$\left(x+\frac{p}{2}\right)^2 = \left(\frac{p}{2}\right)^2-q$ ,

sodass wir im nächsten Schritt die Wurzel ziehen können und die pq Formel als Ergebnis erhalten

$x + \frac{p}{2} = \pm \sqrt{\left(\frac{p}{2}\right)^2-q}$

$\Rightarrow x_{1,2} =- \frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2-q}$ .

pq Formel Aufgaben

Jetzt kennst du schon die Erklärung der pq Formel kannst die pq Formel anwenden. Im Folgenden findest du verschiedene Aufgaben und Lösungen zum Thema pq Formel.

Aufgabe 1

Löse die Folgenden quadratischen Gleichungen, indem du die pq-Formel verwendest:

a) x²+2x=-1

b) -x²+13x-30=0

Aufgabe 2

Gib jeweils an, wie viele Nullstellen die quadratischen Funktionen besitzen, ohne sie explizit mithilfe der pq-Formel auszurechnen:

a) f(x)=x²+4x+5

b) f(x)=x²+3x-4

Lösungen

Aufgabe 1

a) Um die quadratische Gleichung x²+2x=-1 mittels pq-Formel zu lösen, bringen wir sie zuerst auf Normalform

x²+2x+1=0.

Nun setzen wir p=2 und q=1 in die pqFormel ein

$x_{1,2} =- \frac{2}{2} \pm \sqrt{\left(\frac{2}{2}\right)^2-1} = -1 \pm \sqrt{1-1} = -1\pm 0$ .

Wir erhalten somit eine ein-elementige Lösungsmenge $\mathbb{L}=\{-1\}$ .

b) Bei der Quadratischen Gleichung –x²+13x-30=0 ist Vorsicht geboten. Um sie auf Normalform zu bringen, musst du die komplette Gleichung mit (-1) multiplizieren

x²-13x+30=0.

Jetzt kannst du p=-13 und q=30 in die pq-Formel einsetzen und berechnest

$x_{1,2} =- \frac{-13}{2} \pm \sqrt{\left(\frac{-13}{2}\right)^2-30} = 6,5 \pm \sqrt{(-6,5)^2-30} = 6,5 \pm \sqrt{42,25-30}$ .

$= 6,5 \pm \sqrt{12,25} =6,5\pm 3,5.$

Somit erhältst du zwei Lösungen x₁ =6,5+3,5= 10 und x₂ = 6,5-3,5=3 und die Lösungsmenge $\mathbb{L}=\{3; 10\}$ .

Aufgabe 2

Um die Anzahl der Nullstellen zu bestimmen, betrachten wir die Diskriminante $D=\left(\frac{p}{2}\right) ^2-q$ der pq-Formel.

a) Durch Einsetzen der Werte p=4 und q=5 in die Formel der Diskriminante, siehst du sofort, dass die zugehörige Parabel keine Nullstellen hat, da D<0, denn

$D=\left(\frac{4}{2}\right)^2-5 = 2^2-5 = 4-5 = -1 <0.$

b) In diesem Fall setzen wir p=3 und q=-4 in die Diskriminante ein und erhalten

$D=\left(\frac{3}{2}\right)^2-(-4) =1,5^2+4 = 6,25>0.$

Da D>0 ist, hat diese Parabel zwei Nullstellen.

Satz von Vieta

Möchtest du schnell überprüfen, ob deine Lösungen, die du mit der pq-Formel bestimmt hast, stimmen? Dann hilft dir der Satz von Vieta . Der sagt nämlich, dass wieder -p rauskommen muss, wenn du die Lösungen zusammen rechnest:

-p = x₁ + x₂

Gleichzeitig muss aber auch folgender Zusammenhang gelten:

q = x₁ · x₂

Schau dir dafür nochmal das Beispiel vom Anfang an:

x²+ 2x -3 =0

Die pq-Formel hat als Lösungsformel für quadratische Gleichungen folgende Lösungen ergeben:

x₁ = 1 und x₂ = -3

Willst du testen, ob die Lösung stimmt, kannst du den Satz von Vieta verwenden:

$-p=-2\stackrel{?}{=}1+\left(-3\right)=-2\checkmark$

$q=-3\stackrel{?}{=}1\cdot\left(-3\right)=-3\checkmark$

Die Lösungen stimmen also!

abc-Formel

Wenn du eine quadratische Gleichung der Form ax² + bx + c = 0 gegeben hast, kannst du auch die Mitternachtsformel oder die ABC-Formel anwenden.

$x_{1,2} = \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

In unserem Video zur abc Formel erklären wir dir Schritt für Schritt anhand vieler Beispiele, wie die Formel angewendet wird. Du willst nie wieder Probleme mit dem Lösen quadratischer Gleichungen haben? Dann schau es dir direkt an!