Magnetischer Fluss
Der magnetische Fluss beschreibt „wie viel magnetisches Feld durch eine Fläche tritt“. Was er genau ist und wie die wichtigsten Formeln aussehen, erfährst du in unserem Beitrag. Hier geht es direkt zum Video !
Inhaltsübersicht
Magnetischer Fluss einfach erklärt
Stell dir vor, du hast ein magnetisches Feld
 . Du kannst es mit Hilfe von Feldlinien veranschaulichen. Wenn du das magnetische Feld „stärker“ machst, hast du auch mehr Feldlinien.
. Du kannst es mit Hilfe von Feldlinien veranschaulichen. Wenn du das magnetische Feld „stärker“ machst, hast du auch mehr Feldlinien.
Jetzt stellst du dir gedanklich eine Fläche  vor, die du senkrecht zu deinem magnetischen Feld platzierst. Der magnetische Fluss
vor, die du senkrecht zu deinem magnetischen Feld platzierst. Der magnetische Fluss  beschreibt dann die Menge der Feldlinien (Menge des Magnetfeldes
beschreibt dann die Menge der Feldlinien (Menge des Magnetfeldes  ), die deine Fläche
), die deine Fläche  senkrecht durchtreten.
senkrecht durchtreten.
Vergrößerst du also die Fläche  , schaffen es mehr Feldlinien (also mehr Magnetfeld) durch die Fläche. Wenn du hingegen das Magnetfeld
, schaffen es mehr Feldlinien (also mehr Magnetfeld) durch die Fläche. Wenn du hingegen das Magnetfeld  größer machst, hast du zwar dieselbe Fläche, aber nun mehr Feldlinien. Also schaffen es wieder mehr Feldlinien durch die Fläche.
größer machst, hast du zwar dieselbe Fläche, aber nun mehr Feldlinien. Also schaffen es wieder mehr Feldlinien durch die Fläche.
Formal ist der magnetische Fluss  bei senkrechtem Einfall gleich das Produkt aus magnetischem Feld
bei senkrechtem Einfall gleich das Produkt aus magnetischem Feld  und Fläche
und Fläche 
 .
.
Trifft das magnetisches Feld nicht senkrecht auf die Fläche, sondern unter einem Winkel  , dann berechnest du den magnetischen Fluss
, dann berechnest du den magnetischen Fluss  als magnetisches Feld
als magnetisches Feld  mal Fläche
mal Fläche  mal dem Kosinus des Winkels
mal dem Kosinus des Winkels  . Die Einheit von Phi ist das Weber.
. Die Einheit von Phi ist das Weber.
Magnetischer Fluss 
Einheit Magnetischer Fluss ![Rendered by QuickLaTeX.com [\Phi] = \text{Wb}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1c01b86889780425793aa326c4596781_l3.png)
Wichtig: Das magnetische Feld muss homogen und die Fläche darf nicht gebogen sein.
Magnetischer Fluss Phi
Mit dem magnetischen Fluss  (das Formelzeichen ist das griechische Phi) kannst du bei gegebener Fläche
(das Formelzeichen ist das griechische Phi) kannst du bei gegebener Fläche  und gegebenen magnetischen Feld
und gegebenen magnetischen Feld  berechnen, wie viel des Magnetfeldes es durch die Fläche schafft.
berechnen, wie viel des Magnetfeldes es durch die Fläche schafft.
Im einfachen Fall, dass es zwischen  und
und  keinen Winkel gibt, kannst du Phi so berechnen
keinen Winkel gibt, kannst du Phi so berechnen
 .
.
Wenn aber das Magnetfeld  in einem Winkel
in einem Winkel  auf die Fläche
auf die Fläche  trifft, dann ändert sich die Formel etwas. Du musst hier noch einen Faktor von
trifft, dann ändert sich die Formel etwas. Du musst hier noch einen Faktor von  einbauen
einbauen
 .
.
Der Faktor garantiert, dass du vom Magnetfeld nur diejenige Komponente berücksichtigst, die auch senkrecht zur Fläche steht.
Im Allgemeinen ist es nicht einfach, Phi zu bestimmen. Theoretisch müsstest du an jedem Punkt der Fläche den Winkel  neu bestimmen. Es gibt aber ein paar einfache und sehr wichtige Beispiele, bei denen du den magnetischen Fluss ohne großen Aufwand berechnen kannst.
neu bestimmen. Es gibt aber ein paar einfache und sehr wichtige Beispiele, bei denen du den magnetischen Fluss ohne großen Aufwand berechnen kannst.
Magnetischer Fluss Leiterschleife und Spule
Eines dieser Beispiele ist die Leiterschleife. Sie besteht aus einer einfachen geometrischen Form. Das könnte zum Beispiel ein Rechteck oder ein Kreis ein. Die Leiterschleife besitzt eine Fläche  und befindet sich in einem homogenen Magnetfeld
und befindet sich in einem homogenen Magnetfeld  .
.
Wegen der einfachen Geometrie und der Homogenität von  musst du den Winkel
musst du den Winkel  nur einmal bestimmen. Ein homogenes Feld ist es überall gleich stark und zeigt in eine fixe Richtung. Deshalb kannst du hier den magnetischen Fluss Phi leicht ausrechnen
nur einmal bestimmen. Ein homogenes Feld ist es überall gleich stark und zeigt in eine fixe Richtung. Deshalb kannst du hier den magnetischen Fluss Phi leicht ausrechnen
 ,
,
wobei  die Fläche des Rechtecks
oder die Fläche des Kreises
ist.
die Fläche des Rechtecks
oder die Fläche des Kreises
ist.
Wenn du dir jetzt  -viele solcher Leiterschleifen nimmst, kannst du sie aufeinander stapeln. Du erhältst so eine Spule. Wenn wir bei einem homogenen Feld bleiben, dann kannst du auch hier den magnetischen Fluss leicht bestimmen
-viele solcher Leiterschleifen nimmst, kannst du sie aufeinander stapeln. Du erhältst so eine Spule. Wenn wir bei einem homogenen Feld bleiben, dann kannst du auch hier den magnetischen Fluss leicht bestimmen
 .
.
Du nimmst also den magnetischen Fluss der Leiterschleife und multiplizierst ihn mit  . Du findest für
. Du findest für  auch die Bezeichnung Windungen.
auch die Bezeichnung Windungen.
Beachte: Das  wird auch magnetische Flussdichte genannt. Verwechsle das auf keinen Fall mit dem magnetischen Fluss Phi. Die Flussdichte ist ein Maß dafür, wie stark das magnetische Feld
ist.
wird auch magnetische Flussdichte genannt. Verwechsle das auf keinen Fall mit dem magnetischen Fluss Phi. Die Flussdichte ist ein Maß dafür, wie stark das magnetische Feld
ist.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Einheit Magnetischer Fluss
Werfen wir einen kurzen Blick auf die Einheit. Das magnetische Feld  hat die Einheit Tesla (
hat die Einheit Tesla ( ) und die Fläche die Einheit Quadratmeter (
) und die Fläche die Einheit Quadratmeter ( ). Als Produkt von
). Als Produkt von  und
und  hat magnetischer Fluss somit die Einheit
hat magnetischer Fluss somit die Einheit
![Rendered by QuickLaTeX.com [\Phi] = \text{T} \cdot \text{m}^2](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2e5bc5d185cd439653a8efb9ea6eed1a_l3.png) .
.
Dem Produkt aus Tesla und Quadratmeter wurde die kürzere Einheit Weber ( ) gegeben. Wir haben also
) gegeben. Wir haben also
![Rendered by QuickLaTeX.com [\Phi] = \text{Wb}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1c01b86889780425793aa326c4596781_l3.png) .
.
Magnetischer Fluss Abhängigkeiten
Anhand der Formel erkennst du, dass magnetischer Fluss von drei Größen abhängt: Dem magnetischen Feld  , der Fläche
, der Fläche  und dem Winkel
und dem Winkel  .
.
Der magnetische Fluss hängt dabei linear von  und
und  ab. Wenn du zum Beispiel die Fläche
ab. Wenn du zum Beispiel die Fläche  vergrößerst, aber das magnetische Feld
vergrößerst, aber das magnetische Feld  und den Winkel
und den Winkel  gleich lässt, so hast du einen größeren magnetischen Fluss. Eine große Fläche bedeutet also ein großer Fluss und eine kleine Fläche einen kleinen Fluss.
gleich lässt, so hast du einen größeren magnetischen Fluss. Eine große Fläche bedeutet also ein großer Fluss und eine kleine Fläche einen kleinen Fluss.
Vergrößerst du hingegen das magnetische Feld  , so wird auch der magnetische Fluss größer. Ein starkes Magnetfeld führt zu einem großen Fluss, ein schwaches Feld zu einem kleinen Fluss.
, so wird auch der magnetische Fluss größer. Ein starkes Magnetfeld führt zu einem großen Fluss, ein schwaches Feld zu einem kleinen Fluss.
Insgesamt gilt also: Je größer du das Magnetfeld  oder die Fläche
oder die Fläche  machst, desto höher der magnetische Fluss.
machst, desto höher der magnetische Fluss.
Die Situation mit dem Winkel  ist etwas komplizierter. Stell dir vor, deine Fläche steht senkrecht zum Magnetfeld, dein Winkel ist dann
ist etwas komplizierter. Stell dir vor, deine Fläche steht senkrecht zum Magnetfeld, dein Winkel ist dann  . Hier hast du den größten magnetischen Fluss. Wenn du jetzt schrittweise den Winkel vergrößerst, nimmt der magnetische Fluss ab. Erreichst du
. Hier hast du den größten magnetischen Fluss. Wenn du jetzt schrittweise den Winkel vergrößerst, nimmt der magnetische Fluss ab. Erreichst du  ist der magnetische Fluss gleich Null, da sich das Magnetfeld parallel zur Fläche befindet. Danach beginnt er wieder größer zu werden.
ist der magnetische Fluss gleich Null, da sich das Magnetfeld parallel zur Fläche befindet. Danach beginnt er wieder größer zu werden.
Magnetischer Fluss Skalarprodukt
Wenn du zwei Vektoren
 und
und  hast, dann kannst du das Skalarprodukt
berechnen
hast, dann kannst du das Skalarprodukt
berechnen
 .
.
Ist dir die Ähnlichkeit zur Formel für den magnetischen Fluss aufgefallen? Das ist kein Zufall. Du kannst nämlich die Formel  kompakter auch so schreiben
kompakter auch so schreiben
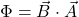 .
.
Vielleicht ist dir das magnetische Feld als Vektor vertraut. Du kannst dir aber auch eine Fläche als Vektor vorstellen. An jedem Punkt entlang der Fläche kannst du Vektoren befestigen, die an diesem Punkt senkrecht zur Fläche stehen.
Eine Aussage wie „ zeigt in Richtung
zeigt in Richtung  “ bedeutet dann, dass der Vektor
“ bedeutet dann, dass der Vektor  parallel zum Vektor
parallel zum Vektor  ist.
ist.
Induktionsgesetz und Induktionsspannung
Der magnetische Fluss kann sich also ändern, wenn sich das magnetische Feld  , die Fläche
, die Fläche  oder der Winkel
oder der Winkel  ändern. Das führt zu einer zentralen Beobachtung, dem Induktionsgesetz.
ändern. Das führt zu einer zentralen Beobachtung, dem Induktionsgesetz.
Ändert sich nämlich der magnetische Fluss zeitlich, so führt das zu einer (messbaren) Spannung, der sogenannten Induktionsspannung
 .
.
Für den Fall der Spule mit  Windungen hast du
Windungen hast du
 .
.
Ein gutes Beispiel für das Phänomen der Induktion ist die Bewegung einer Leiterschleife in einem Magnetfeld. Du findest das und mehr ausführlich in unserem Beitrag zum Induktionsgesetz erklärt.



