Flächeninhalt Kreis
Du möchtest den Flächeninhalt eines Kreises berechnen? Hier im Beitrag und im Video erfährst du es!
Inhaltsübersicht
Flächeninhalt eines Kreises — einfach erklärt
Der Flächeninhalt vom Kreis berechnest du mit der folgenden Formel:
A = π • r2
Der Radius r ist der Abstand vom Mittelpunkt M zur Kreislinie. Den Flächeninhalt A vom Kreis berechnest du mit der Kreiszahl π (≈ 3,14).
Schauen wir uns mal an, wie du den Flächeninhalt jeweils mit gegebenem Radius, Durchmesser und Umfang berechnen kannst.
Flächeninhalt eines Kreises mit Radius berechnen
Wenn du den Radius eines Kreises gegeben hast, musst du ihn nur in die Formel einsetzen, um die Fläche des Kreises zu berechnen.
➡️ Beispiel:
Berechne den Flächeninhalt vom Kreis mit Radius r = 3 cm.
A = π • r2 | Kreisfläche Formel aufstellen
A = π • (3 cm)2 | Radius einsetzen
A = π • 9 cm2 ≈ 28,27 cm2 | Kreisinhalt berechnen
Dieser Kreis hat einen Flächeninhalt von rund 28,27 cm2.
Beachte: Im letzten Schritt nimmst du die Einheit hoch zwei und erhältst deshalb cm2 statt cm.
Flächeninhalt eines Kreises mit Durchmesser berechnen
Manchmal hast du zum Berechnen des Flächeninhalts nicht den Radius, sondern den Durchmesser d gegeben. Das ist der Abstand von einer Seite des Kreises zur anderen. Er ist immer genau doppelt so groß wie der Radius: d = 2 • r.
Den Flächeninhalt A eines Kreises mit Durchmesser d berechnest du mit der Formel:
A = (d : 2)2 • π
➡️ Beispiel:
Berechne den Flächeninhalt vom Kreis mit Durchmesser d = 7 cm.
![\[\textcolor{red}{A} =\left(\cfrac{\textcolor{orange}{d}}{2}\right)^2 \cdot \pi\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-17e2a9e23115306b52536bc9f0179d3e_l3.png "Rendered by QuickLaTeX.com")
![\[\textcolor{red}{A} = \left(\cfrac{\textcolor{orange}{7 cm}}{2}\right)^2 \cdot \pi\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d12d4ef04a64ec4e4b3cfac20e9e2835_l3.png "Rendered by QuickLaTeX.com")
![\[\textcolor{red}{A} = \left(3,5 cm)^2 \cdot \pi \approx 38,48 cm^2\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-36d6c8f01724418966dafb846bce03bf_l3.png "Rendered by QuickLaTeX.com")
Der Flächeninhalt von diesem Kreis beträgt also rund 38,48 cm2.
Flächeninhalt eines Kreises mit Umfang berechnen
Du kannst den Flächeninhalt auch aus dem Umfang U bestimmen. Dafür verwendest du die Formel:
A = U 2 : (4π)
➡️ Beispiel:
Berechne den Flächeninhalt vom Kreis mit dem Umfang U = 62,83 cm.
![\[\textcolor{red}{A} = \cfrac{\textcolor{olive}{U}^2}{4 \pi}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-70b4e99e40768042a11395d94b751173_l3.png "Rendered by QuickLaTeX.com")
![\[\textcolor{red}{A} = \cfrac{(\textcolor{olive}{62,83\,cm})^2}{4 \pi}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e4d937892e05f86c3ef494bec993bb44_l3.png "Rendered by QuickLaTeX.com")
![\[\textcolor{red}{A} \approx 314,14\,cm^2\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-6ad9171d6b5bf22f06a2202c486bbbd5_l3.png "Rendered by QuickLaTeX.com")
Der Flächeninhalt des Kreises beträgt rund 314,14 cm2.
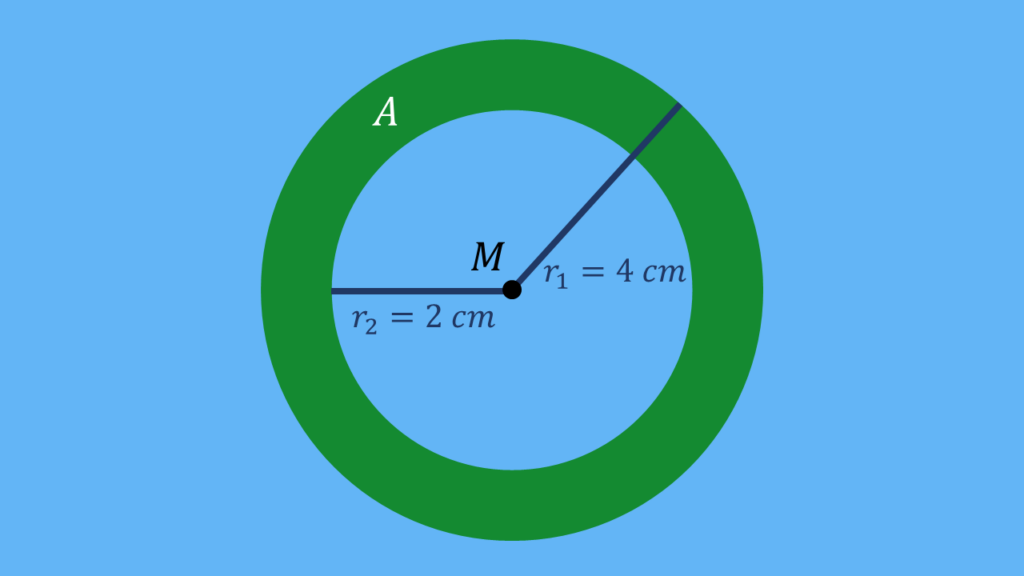
Kreisring berechnen
Es gibt auch die Möglichkeit, dass die Kreisfläche nicht ganz gefüllt ist, sondern ein Loch in der Mitte hat. So eine Figur nennst du einen Kreisring.
Die Fläche des Kreisrings kannst du mit der folgenden Formel berechnen:
AKreisring = Agroß – Aklein
Das heißt, du ziehst von der großen Kreisfläche den Flächeninhalt vom kleinen Kreis (“Loch“) ab.
➡️ Beispiel:
Die große Kreisfläche hat einen Radius von r1 = 4 cm und die kleine von r2 = 2 cm.
1. Flächeninhalt vom großen Kreis berechnen:
Agroß = π • r12 = π • (4 cm)2 ≈ 50,27 cm2
2. Kreisfläche des Lochs bestimmen:
Aklein = π • r22 = π • (2 cm)2 ≈ 12,57 cm2
3. Flächeninhalt Kreisring ausrechnen:
AKreisring = Agroß – Aklein = 50,27 cm2 – 12,57 cm2 = 37,7 cm2
Der Flächeninhalt von dem Kreisring beträgt 37,7 cm2.
Hinweis: Du kannst diese Formel auch anwenden, wenn das Loch des Kreisrings nicht genau in der Mitte des großen Kreises liegt.
Flächeninhalt Kreis — häufigste Fragen
-
Wie wird der Flächeninhalt eines Kreises berechnet? Der Flächeninhalt vom Kreis ist die Größe der Kreisfläche A = π • r2. -
Wie wird der Flächeninhalt eines Kreises mit dem Durchmesser berechnet? Kreisfläche berechnen mit Durchmesser: A = (d : 2)2 • π
Der Durchmesser d ist der Abstand von einer Seite des Kreises zur anderen. Er ist immer genau doppelt so groß wie der Radius: d = 2 • r.
Kreisberechnung
In unserem Video zur Kreisberechnung findest du alle wichtigen Kreisformeln noch einmal erklärt, zum Beispiel die Kreisfläche und den Kreisumfang.
