Vektor
In diesem Beitrag erklären wir dir, was ein Vektor ist und was du mit ihm beschreiben kannst.
Du möchtest in kurzer Zeit alles Wichtige zum Thema Vektor erfahren? Dann schau dir unser Video dazu an!
Inhaltsübersicht
Vektor einfach erklärt
Wähle einen Punkt im Koordinatensystem aus und verschiebe ihn in irgendeine Richtung. Dabei hast du eine Änderung in der x- und y-Koordinate. Diese Verschiebung des Punktes wird Vektor genannt.
Mit einem Vektor kannst du von einem Ausgangspunkt alle Punkte im Raum beschreiben. Ein Vektor in einem Koordinatensystem wird mit einem Pfeil dargestellt.
Hinweis: Man unterscheidet Vektoren und Skalare. Ein Skalar stellt dabei einfach eine Zahl dar.
Was ist ein Vektor?
Stell dir vor, du hast einen Punkt A gegeben, und musst nun einen anderen Punkt B wählen, der eine bestimmte Länge von Punkt A entfernt ist. Verbindest du die beiden Punkte, so erhältst du die Strecke  . Allerdings kannst du aus der Ansicht nicht erkennen, ob die Strecke nun in Richtung B oder in Richtung A verläuft. Um das zu markieren, fügst du eine Pfeilspitze ein. Damit verdeutlichst du in welche Richtung die Strecke geht. Im unteren Bild von A nach B. Dieser Pfeil heißt Vektor von A nach B.
. Allerdings kannst du aus der Ansicht nicht erkennen, ob die Strecke nun in Richtung B oder in Richtung A verläuft. Um das zu markieren, fügst du eine Pfeilspitze ein. Damit verdeutlichst du in welche Richtung die Strecke geht. Im unteren Bild von A nach B. Dieser Pfeil heißt Vektor von A nach B.
Eine Größe, die durch ihre Länge und Richtung gegeben ist, heißt Vektor.
Zwei Vektoren sind gleich, wenn sie die gleiche Länge haben und in die gleiche Richtung zeigen.
Als Notation für Vektoren verwendest du entweder Kleinbuchstaben mit einem Pfeil darüber, wie zum Beispiel  oder den Start- und Endpunkt eines Vektors mit einem Pfeil darüber, zum Beispiel
oder den Start- und Endpunkt eines Vektors mit einem Pfeil darüber, zum Beispiel  .
.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Lage von Vektoren
Im folgenden Abschnitt erklären wir dir, wie verschiedene Vektoren zueinander liegen können.
Ein Vektor  ist parallel zu einem Vektor
ist parallel zu einem Vektor  , wenn er entweder in die gleiche oder in die entgegengesetzte Richtung (
, wenn er entweder in die gleiche oder in die entgegengesetzte Richtung ( ) zeigt.
) zeigt.
Ein Vektor  heißt Gegenvektor zu einem Vektor
heißt Gegenvektor zu einem Vektor  , wenn
, wenn  parallel zu
parallel zu  ist, gleich lang ist und in die entgegengesetzte Richtung zeigt. Dabei ist der Gegenvektor von
ist, gleich lang ist und in die entgegengesetzte Richtung zeigt. Dabei ist der Gegenvektor von  gleich
gleich  . Es ist also
. Es ist also 
Zwei Vektoren  und
und  stehen senkrecht
aufeinander, wenn der Winkel, den die beiden Vektoren einspannen,
stehen senkrecht
aufeinander, wenn der Winkel, den die beiden Vektoren einspannen,  beträgt.
beträgt.
Vektoren in einem Koordinatensystem
In einem Koordinatensystem kannst du jeden Punkt durch seine Koordinatendarstellung  beschreiben. Dabei ist der Punkt A um
beschreiben. Dabei ist der Punkt A um  Längeneinheiten entlang der x-Achse, und um
Längeneinheiten entlang der x-Achse, und um  Längeneinheiten entlang der y-Achse vom Ursprung
Längeneinheiten entlang der y-Achse vom Ursprung  aus verschoben. Damit definiert der Punkt A also einen Vektor
aus verschoben. Damit definiert der Punkt A also einen Vektor
 .
.
Dabei stellt  die Verschiebung in der x-Achse und
die Verschiebung in der x-Achse und  die Verschiebung in der y-Achse dar.
die Verschiebung in der y-Achse dar.
Analog gilt das auch für die Vektoren im Raum

Beispiel
Startest du am Ursprung und gehst -1 Längeneinheiten entlang der x-Achse und 3 Längeneinheiten entlang der y-Achse, so landest du beim Punkt  und damit hast du den Vektor
und damit hast du den Vektor

Oder betrachtest du zum Beispiel den Punkt  . Dieser ist um 4 entlang der x-Achse und um -1 entlang der y-Achse verschoben. Dieser Punkt wird durch folgenden Vektor beschrieben.
. Dieser ist um 4 entlang der x-Achse und um -1 entlang der y-Achse verschoben. Dieser Punkt wird durch folgenden Vektor beschrieben.

Vektoren durch zwei Punkte berechnen
Hier zeigen wir dir, wie du einen Vektor berechnen kannst, wenn du zwei Punkte zur Verfügung hast.
Hast du zwei Punkte  und
und  gegeben, so kannst du den Vektor
gegeben, so kannst du den Vektor  folgendermaßen berechnen.
folgendermaßen berechnen.

Um den Vektor zwischen zwei Punkten zu berechnen, rechnest du Pfeilspitze minus Fuß.
Beispiel
Betrachte zum Beispiel die zwei Punkte  und
und  . Um die Verschiebung in der x-Achse zu berechnen, rechnest du einfach die x-Koordinate von B minus die x-Koordinate von A.
. Um die Verschiebung in der x-Achse zu berechnen, rechnest du einfach die x-Koordinate von B minus die x-Koordinate von A.
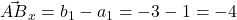
Das gleiche machst du auch, um die Verschiebung in der y-Achse zu berechnen. Du rechnest also die y-Koordinate von B minus die y-Koordinate von A.
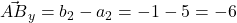
Somit erhältst du den Vektor

Unterschied Ortsvektor und Richtungsvektor
Man unterscheidet zwischen zwei Arten von Vektoren: Ortsvektoren und Richtungsvektoren/Verbindungsvektoren.
Ortsvektoren haben ihren Startpunkt immer am Ursprung und werden mit  oder
oder  bezeichnet. So lautet zum Beispiel der Ortsvektor zum Punkt
bezeichnet. So lautet zum Beispiel der Ortsvektor zum Punkt 

Richtungsvektoren bzw. Verbindungsvektoren hingegen können ihren Startpunkt an jedem beliebigen Punkt haben und haben dementsprechend in ihrer Notation den Start- und Endpunkt, wie etwa  . Zum Beispiel lautet der Richtungsvektor zwischen
. Zum Beispiel lautet der Richtungsvektor zwischen  und
und 

Länge eines Vektors
Ein Vektor besitzt immer eine gewissen Länge. Wenn du also einen Vektor  gegeben hast, so kannst du seine Länge wie folgt berechnen.
gegeben hast, so kannst du seine Länge wie folgt berechnen.

Das heißt, du quadrierst erst die Komponenten des Vektors und ziehst dann von der Summe die Wurzel.
Beispiel
Es sei der Vektor  gegeben und du willst jetzt seine Länge bestimmen. Du rechnest also
gegeben und du willst jetzt seine Länge bestimmen. Du rechnest also

Möchtest du mehr Beispiele sehen? Dann schau dir unseren extra Beitrag Betrag eines Vektors dazu an!
Skalarprodukt
Das Skalarprodukt
ist eine Abbildung, die zwei Vektoren nimmt und daraus eine reelle Zahl produziert. Hast du zwei Vektoren  und
und  gegeben, so ist das Skalarprodukt wie folgt definiert.
gegeben, so ist das Skalarprodukt wie folgt definiert.

Ist dabei das Skalarprodukt gleich 0, so stehen die zwei Vektoren senkrecht aufeinander.
Das Skalarprodukt kann dir dabei helfen, die Länge eines Vektors zu bestimmen, denn für die Länge rechnest du

Eine weitere Verwendung des Skalarprodukts ist die Berechnung des Winkels  zwischen zwei Vektoren
zwischen zwei Vektoren  und
und  . Dafür benutzt du die Formel
. Dafür benutzt du die Formel

die im Zähler das Skalarprodukt der beiden Vektoren  und
und  enthält.
enthält.
Beispiel
Betrachte die Vektoren 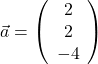 und
und  . Ihr Skalarprodukt lautet
. Ihr Skalarprodukt lautet

Da das Skalarprodukt gleich 0 ist, stehen die beiden Vektoren senkrecht aufeinander.
Vektor Linearkombination
Wie du in den vorherigen Abschnitt gesehen hast, kannst du Vektoren addieren, subtrahieren
und mit einem Vielfachen multiplizieren. Dabei heißt jede Summe von Vektoren  Linearkombination
.
Linearkombination
.

 sind dabei irgendwelche Zahlen.
sind dabei irgendwelche Zahlen.
Lineare Abhängigkeit und Unabhängigkeit von Vektoren
Vektoren  bis
bis  heißen linear abhängig
, wenn sich einer der Vektoren durch eine Linearkombination der anderen darstellen lässt. Wenn du zum Beispiel zwei Vektoren
heißen linear abhängig
, wenn sich einer der Vektoren durch eine Linearkombination der anderen darstellen lässt. Wenn du zum Beispiel zwei Vektoren  und
und 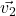 hast, so sind sie linear abhängig, wenn es ein
hast, so sind sie linear abhängig, wenn es ein  gibt, sodass
gibt, sodass

Graphisch veranschaulicht bedeutet das, dass sie entweder in die gleiche oder entgegengesetzte Richtung zeigen (blauer und lila Vektor). Dagegen sind sie linear unabhängig, wenn sie in zwei verschiedene Richtungen zeigen (blauer und grüner Vektor).
Drei Vektoren  ,
, 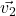 und
und  sind linear abhängig, wenn es ein
sind linear abhängig, wenn es ein  und ein
und ein  gibt, sodass
gibt, sodass

Graphisch bedeutet das, dass alle drei Vektoren in der gleichen Ebene liegen (blaue und grüne Vektoren), zeigt jedoch ein Vektor aus der Ebene heraus, so sind sie linear unabhängig (blaue und lila Vektoren).
Vektor Kreuzprodukt
Das Kreuzprodukt
zweier Vektoren  und
und  liefert dir ein Vektor, der sowohl senkrecht zu
liefert dir ein Vektor, der sowohl senkrecht zu  als auch senkrecht zu
als auch senkrecht zu  steht. Das Kreuzprodukt berechnet sich folgendermaßen.
steht. Das Kreuzprodukt berechnet sich folgendermaßen.

Weitere Themen der Vektorrechnung
Es gibt noch weitere Themen, die sich mit Vektoren beschäftigen. Schau dir unbedingt auch unsere Videos zu den folgenden Themen an:
Vektoren Aufgaben
In diesem Abschnitt geben wir dir zwei Aufgaben, mit denen du die Berechnung eines Vektors üben kannst.
Aufgabe 1: Vektoren berechnen im 
Berechne den Vektor, der durch die zwei Punkte  und
und  gegeben ist.
gegeben ist.
Lösung Aufgabe 1
Um den Vektor zu berechnen, bedienst du dich der Regel „Spitze minus Fuß“. Das heißt, zuerst berechnest du die Verschiebung entlang der x-Achse

und dann die Verschiebung entlang y-Achse

Damit erhältst du dann den Vektor

Aufgabe 2: Vektoren berechnen im 
Du hast die Punkte  ,
,  gegeben. Berechne den dazugehörigen Vektor
gegeben. Berechne den dazugehörigen Vektor  .
.
Lösung Aufgabe 2
Auch in dieser Aufgabe berechnest du den Vektor, indem du die Koordinaten von B minus die Koordinaten von A rechnest. Du rechnest also











 .
. und
und  zu addieren, zählst du die Komponenten Zeile für Zeile zusammen. Du erhältst somit
zu addieren, zählst du die Komponenten Zeile für Zeile zusammen. Du erhältst somit



 um 50% verlängern, so multiplizierst den Vektor mit
um 50% verlängern, so multiplizierst den Vektor mit  . Dabei erhältst du
. Dabei erhältst du




 und
und 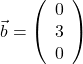 gegeben. Ihr Kreuzprodukt lautet
gegeben. Ihr Kreuzprodukt lautet
