Carnot Prozess
Der Carnot-Kreisprozess spielt eine Hauptrolle in der Thermodynamik. Wie dieser abläuft und wie du ihn berechnen kannst, erfährst du in diesem Beitrag.
Beim Carnot-Prozess handelt es sich um eine ideale Wärme-Kraft-Maschine, welche Wärme in Arbeit umwandelt. Das Ganze ist also ein Gedankenexperiment.
Inhaltsübersicht
Carnotscher Kreisprozess im p-V-Diagramm
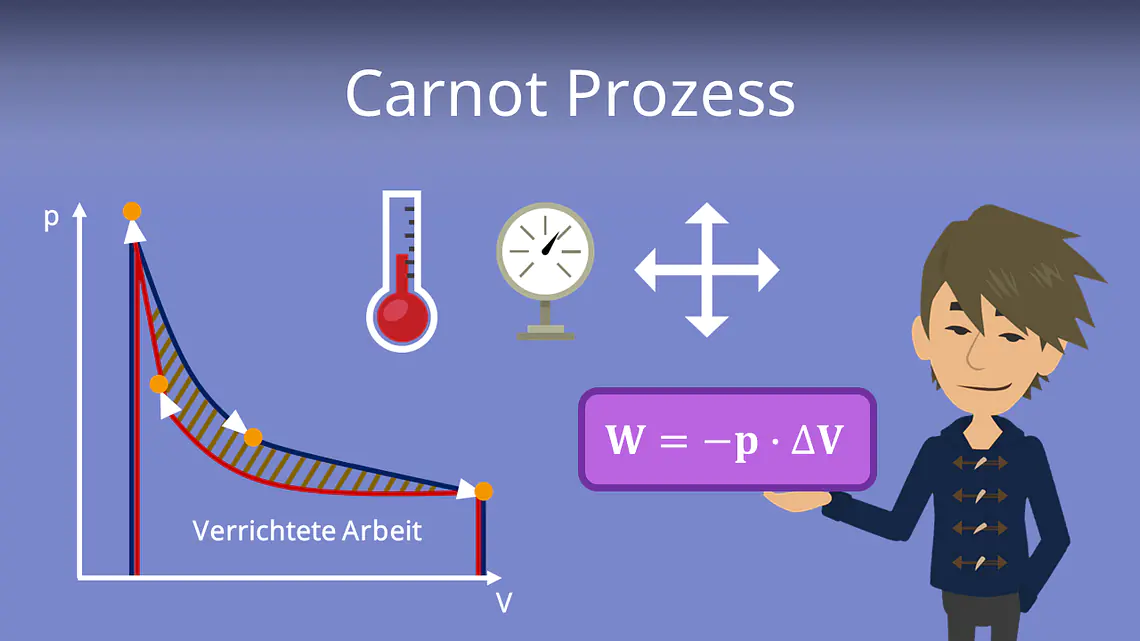
Fangen wir mit der Betrachtung des p-V-Diagramms an. Im Kreisprozess laufen zwei isotherme und zwei reversible adiabatische bzw. isentrope Zustandsänderungen ab.
Die 4 Prozessschritte bzw. Takte beim Carnot Prozess sind:
- Isotherme Kompression
- Isentrope Kompression
- Isotherme Expansion
- Isentrope Expansion
Isotherme Kompression 1 -> 2:
Bei der ersten Zustandsänderung von 1 nach 2 läuft eine isotherme Kompression ab.
Die Temperatur bleibt konstant während sich der Druck und das Volumen ändern. Durch die verrichtete Arbeit W12 in Form der Kompression wird dem System Energie zugeführt. Die Arbeit ist proportional zur Volumenänderung:

Damit die Temperatur nun konstant bleiben kann, muss Wärmeenergie Q12 abgeführt werden.
Isentrope Kompression 2 -> 3:
Im nächsten Schritt von 2 nach 3 läuft eine isentrope Kompression ab. Das Volumen wird also weiterhin komprimiert. Die Temperatur steigt auf T2, der Druck wird immer noch größer und das Volumen sinkt minimal weiter. Da diese Zustandsänderung isentrop abläuft, gibt es keinen Wärmeaustausch mit der Umgebung, es gilt also:

Die Arbeit für die Kompression liefert W23.
Isotherme Expansion 3 -> 4:
Die nächste Zustandsänderung von 3 nach 4 läuft wieder isotherm ab. Diesmal expandiert das Gas und verrichtet dabei Arbeit W34. Damit das Gas nicht abkühlt, muss nun Wärme Q34 zugeführt werden. Die Temperatur bleibt also konstant, während das Volumen steigt und der Druck sinkt.
Isentrope Expansion 4 -> 1:
Im letzten Schritt von 4 nach 1 kommt es zu einer isentropen Expansion des Gases. Die Temperatur sinkt wieder auf T1 ab, da kein Wärmeaustausch stattfindet und dem System durch die verrichtet Arbeit W41 Energie entzogen wird.
Untersuchen wir nun wieviel Energie in Arbeit umgesetzt wird. Integrieren wir die Funktion des Prozesses, dann erhalten wir die verrichtete Arbeit. Einfacher gesagt entspricht die Fläche unter den Kurven der verrichteten Arbeit.
Die verrichtete netto Arbeit entspricht der zugeführten minus der abgeführten Arbeit und wird durch die umschlossene Fläche der Kurven dargestellt.
Carnot Prozess im T-S-Diagramm
Da wir uns im p-V-Diagramm leider nicht die transferierte Wärmeenergie, sondern nur die verrichtete Arbeit herleiten können, betrachten wir das T-S-Diagramm. In diesem wird die Temperatur über die Entropie aufgetragen. Aus der Entropieänderung können wir später die zu- bzw. abgeführte Wärmeenergie nach der folgenden Formel berechnen:

Da es sich außerdem um einen reversiblen, reibungsfreien Prozess handelt, gilt  .
.
Beim p-V-Diagramm haben wir gelernt, dass die Fläche unter den Kurven der verrichteten Arbeit entspricht. Im Fall des T-S-Diagramms gilt dasselbe, nur für die Wärmeenergie. Tragen wir die Zustandsänderungen in das T-S-Diagramm ein, dann erhalten wir die beiden Temperaturstufen T1 und T2.
Die beiden isothermen Zustandsänderungen laufen bei derselben Temperatur ab und da sich die Entropie ändert, kommt es zum Wärmetransfer. Im Diagramm sind das die Pfeile von  und von
und von  .
.
- Für die Zustandsänderung der isothermen Kompression 1 -> 2 gilt mit obiger Formel:

Anhand des Diagramms sehen wir, dass die Entropie im Zustand 1 dem Wert S_2 entspricht und im Zustand 2 den Wert  annimmt. Mit diesen Integrationsgrenzen ergibt sich für die Wärmeenenergie ein negativer Wert.
annimmt. Mit diesen Integrationsgrenzen ergibt sich für die Wärmeenenergie ein negativer Wert.  muss abgeführt werden.
muss abgeführt werden.
- Bei der isothermen Expansion 3 -> 4 wird die zugeführte Wärmeenergie beschrieben als:

Bei den isentropen Zustandsänderungen 2 -> 3 und 4 -> 1 ändert sich die Temperatur, während die Entropie gleichbleibt. In unserem Diagramm musst du dir hier die Linien von  und von
und von  anschauen.
anschauen.
Beziehen wir diese Erkenntnis auf unsere Formel  , dann können wir daraus schließen, dass kein Wärmeaustausch mit der Umgebung stattfindet (
, dann können wir daraus schließen, dass kein Wärmeaustausch mit der Umgebung stattfindet ( ). Die zugeführte Wärme Q34 minus der abgeführten Wärme Q12 entspricht nun der Wärme, die dem System netto hinzugefügt und in die Nettoarbeit umgewandelt wird.
). Die zugeführte Wärme Q34 minus der abgeführten Wärme Q12 entspricht nun der Wärme, die dem System netto hinzugefügt und in die Nettoarbeit umgewandelt wird.
Nutzarbeit des Carnot Prozesses
Der erste Hauptsatz der Thermodynamik lautet:

Nach dem Durchlaufen des Carnot Prozesses stellen sich alle Zustandsgrößen auf ihren ursprünglichen Wert ein. Dementsprechend kann die zeitliche Änderung der inneren Energie gleich Null gesetzt werden (dU=0). Für den Zusammenhang aus Arbeit W und Wärme Q gilt:

Die Nutzarbeit setzt sich aus der zugeführten und der abgeführten Wärme des Carnot Prozesses zusammen. Die Nutzarbeit berechnet sich also wie folgt:

Weitere Vergleichsprozesse
Wirkungsgrad des Carnot Prozesses
Zuletzt überlegen wir uns noch, wie wir den Wirkungsgrad
eines Systems berechnen können. Grundsätzlich gilt, dass die Nettoarbeit dem entspricht, was am Ende rauskommt. Die zugeführte Wärme ist das, was wir reinstecken. Der Wirkungsgrad  ist daher gleich der netto verrichteten Arbeit geteilt durch die zugeführte Wärme:
ist daher gleich der netto verrichteten Arbeit geteilt durch die zugeführte Wärme:

Da die Nettowärme der Nettoarbeit entspricht, gilt:

Setzt man für die Wärme die Gleichung  ein, dann erhalten wir vereinfacht:
ein, dann erhalten wir vereinfacht:

Jetzt weißt du wie du den Wirkungsgrad eines Systems, in welchem ein Carnot-Prozess abläuft, ganz leicht berechnen kannst.
Fassen wir nochmal kurz zusammen was wir gelernt haben:
Der Carnot-Prozess besteht aus zwei isentropen und zwei isothermen Zustandsänderungen. Die verrichtete Arbeit entspricht der Fläche unter der Kurve im p-V-Diagramm und die transferierte Wärme der Fläche unter der Kurve im T-S-Diagramm.





