Wie erkenne ich schnell, ob eine DGL eine Bernoulli-DGL ist?

Eine DGL ist eine Bernoulli-DGL, wenn sie sich in die Form (oder äquivalent mit 0 auf einer Seite) bringen lässt, wobei konstant ist. Entscheidend sind genau zwei Potenzen von : und .

Wann darf ich bei einer Bernoulli-DGL nicht durch y teilen?

Durch darfst du nicht teilen, wenn möglich ist, weil Division durch 0 nicht definiert ist. Prüfe deshalb zuerst, ob eine Lösung der DGL ist, und behandle diese Lösung getrennt. Erst danach darfst du für umformen.

Warum wähle ich bei der Substitution u gleich y hoch 1 minus Alpha?

Die Substitution wird gewählt, weil sie die nichtlineare Bernoulli-DGL in eine lineare DGL für verwandelt. Beim Ableiten entsteht ein Faktor , der sich mit dem -Term der DGL so kombiniert, dass am Ende nur noch und vorkommen.

Welche Fehler passieren oft beim Ableiten von u bei der Substitution?

Häufige Fehler beim Ableiten von sind eine falsch angewendete Kettenregel und ein falscher Exponent. Richtig ist . Zum Beispiel ist falsch, weil dabei die innere Ableitung fehlt.

Wie löse ich die lineare DGL für u mit dem integrierenden Faktor?

Eine lineare DGL löst du mit dem integrierenden Faktor . Dann gilt , also und damit .

Video

Quiz

Bernoulli DGL

Name: Bernoulli DGL
Uploaded: 2026-02-18T15:35:34Z
Duration: 3 min 30 s
Description: Du möchtest wissen, was eine Bernoulli DGL ist und wie du sie lösen kannst? Im Folgenden zeigen wir dir das Vorgehen bei diesen speziellen Differentialgleichungen an einem einfachen Beispiel.

Wichtige Inhalte in diesem Video

Bernoulli Differentialgleichung: Lösung durch Substitutionsfunktion

(00:11)

Beispiel – Lösung der homogenen DGL

(01:40)

Bernoulli Differentialgleichung Beispiel – partikuläre Lösung

(02:31)

Du möchtest wissen, was eine Bernoulli DGL ist und wie du sie lösen kannst? Im Folgenden zeigen wir dir das Vorgehen bei diesen speziellen Differentialgleichungen an einem einfachen Beispiel.

Inhaltsübersicht

Bernoulli Differentialgleichung: Lösung durch Substitutionsfunktion

im Videozur Stelle im Video springen

(00:11)

Eine bernoullische DGL ist eine Differentialgleichung erster Ordnung dieser Form:

$y^\prime+a\left(x\right)\ast\ y+b\left(x\right)\ast\ y^\alpha=0$

a(x) und b(x) sind beliebige Funktionen und Alpha ist eine reelle Zahl. Um diese DGL zu lösen, führen wir die Substitutionsfunktion

$u=y^{1-\alpha}$

ein. Du wirst gleich sehen, warum die Substitution und die Rücksubstitution sinnvoll sind.

Dazu leiten wir zunächst ab. Erst bilden wir die äußere Ableitung und multiplizieren nach der Kettenregel mit der Inneren. Jetzt lösen wir die bernoullische Differentialgleichung nach $y^\prime$ auf und erhalten die explizite Form der DGL. Diesen Ausdruck setzen wir in die Ableitung $u^\prime$ ein.

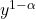Jetzt musst du die DGL etwas umformen, indem du ausmultiplizierst und zusammenfasst. Wie du siehst, heben sich $y^{-\alpha}$ und $y^\alpha$ genau auf, so dass $(1-\alpha \cdot b(x)$ alleine dasteht. Du siehst, dass außerdem $y^{1-\alpha}$ in der DGL auftaucht.

Bernoulli DGL: Rücksubstitution — Rücksubstitution

Das ist genau unsere neu eingeführte Funktion , die wir einsetzen. Nun haben wir alle vorkommenden y-Ausdrücke ersetzt und erhalten eine Differentialgleichung für . Diese wollen wir uns genauer anschauen. Sie sieht gar nicht mehr so kompliziert aus: Es ist eine lineare Differentialgleichung erster Ordnung, die du lösen kannst. Sobald du die Lösung für kennst, kannst du mit Rücksubstitution die Lösung für bestimmen.

$y=u^\frac{1}{1-\alpha}$

Beispiel – Lösung der homogenen DGL

im Videozur Stelle im Video springen

(01:40)

Schauen wir uns ein Beispiel an. Wir betrachten folgende bernoullische DGL:

$y^\prime=y+xy^3$

Unser ergibt sich:

$u=y^{1-\alpha}=y^{1-3}=y^{-2}$

Bernoulli DGL Beispiel — Beispiel Lösung homogener Differentialgleichungen

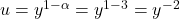
Das kannst du jetzt ableiten. Dann setzt du für $y^\prime$ die Differentialgleichung ein und multiplizierst die Klammer aus. Jetzt setzen wir für $y^{-2}$ das ein und erhalten eine einfache DGL. Die Lösung der homogenen Differentialgleichungen, bestimmst du zum Beispiel mit Trennung der Variablen.

Das sollte inzwischen ein Kinderspiel für dich sein. Du separierst alle u-Anteile und alle x-Anteile auf unterschiedliche Seiten des Gleichheitszeichens:

$\frac{du_h}{u_h}=-2\ dx$

Bernoulli DGL Beispiel: Homogene Lösung — Beispiel: Homogene Lösung

Danach integrierst und stellst das Ergebnis noch nach u_h um. Die homogene Lösung steht.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Bernoulli Differentialgleichung Beispiel – partikuläre Lösung

im Videozur Stelle im Video springen

(02:31)

Bernoulli DGL — häufigste Fragen

(ausklappen)

Wie erkenne ich schnell, ob eine DGL eine Bernoulli-DGL ist?

Eine DGL ist eine Bernoulli-DGL, wenn sie sich in die Form $y' + a(x)\,y = b(x)\,y^\alpha$ (oder äquivalent mit 0 auf einer Seite) bringen lässt, wobei $\alpha$ konstant ist. Entscheidend sind genau zwei Potenzen von : und $y^\alpha$ .
Wann darf ich bei einer Bernoulli-DGL nicht durch y teilen?

Durch darfst du nicht teilen, wenn möglich ist, weil Division durch 0 nicht definiert ist. Prüfe deshalb zuerst, ob $y(x)\equiv 0$ eine Lösung der DGL ist, und behandle diese Lösung getrennt. Erst danach darfst du für $y\neq 0$ umformen.
Warum wähle ich bei der Substitution u gleich y hoch 1 minus Alpha?

Die Substitution $u=y^{1-\alpha}$ wird gewählt, weil sie die nichtlineare Bernoulli-DGL in eine lineare DGL für verwandelt. Beim Ableiten entsteht ein Faktor $y^{-\alpha}y'$ , der sich mit dem $y^\alpha$ -Term der DGL so kombiniert, dass am Ende nur noch und vorkommen.
Welche Fehler passieren oft beim Ableiten von u bei der Substitution?

Häufige Fehler beim Ableiten von $u=y^{1-\alpha}$ sind eine falsch angewendete Kettenregel und ein falscher Exponent. Richtig ist $u'=(1-\alpha)\,y^{-\alpha}\,y'$ . Zum Beispiel ist $u'= (1-\alpha)\,y^{1-\alpha}$ falsch, weil dabei die innere Ableitung fehlt.
Wie löse ich die lineare DGL für u mit dem integrierenden Faktor?

Eine lineare DGL $u' + p(x)\,u = q(x)$ löst du mit dem integrierenden Faktor $\mu(x)=e^{\int p(x)\,dx}$ . Dann gilt $(\mu u)'=\mu q$ , also $\mu u=\int \mu q\,dx + C$ und damit $u=\frac{1}{\mu}\left(\int \mu q\,dx + C\right)$ .

Die partikuläre Lösung kannst du mit einem Ansatz vom Typ der rechten Seite bestimmen. Die Störfunktion

$b\left(x\right)=x$

ist ein Polynom ersten Grades. Also wählst du den Ansatz

$u_p\left(x\right)=a_0+a_1x$

Bernoulli DGL: Partikuläre Lösung — Partikuläre Lösung

Diese Funktion leitest du nun ab. Jetzt setzt du u_p und $u_p^\prime$ in die Differentialgleichung ein. Dann sortierst du alles auf eine Seite und kannst a_1 bestimmen. Anschließend berechnest du noch a_0 . Somit erhältst du die Partikulärlösung. Jetzt noch addieren und es ergibt sich folgende allgemeine Lösung für :