Branch and Bound
Du möchtest dich über das Branch and Bound Verfahren informieren? Dann bist du hier genau richtig! Im folgenden Beitrag stellen wir dir das Branch and Bound Verfahren vor und erklären es dir anhand eines Beispiels.
Inhaltsübersicht
Branch and Bound Verfahren: Erklärung und Beispiel
Bei der Branch and Bound Methode dreht sich alles um die ganzzahlige und kombinatorische Optimierung. Viele Probleme in der Realität sind oft nur ganzzahlig lösbar. Bei der Produktion eines Flugzeugs ist es beispielsweise nicht möglich, 4,2 Flugzeuge herzustellen, sondern nur ganze Anzahlen. Diese Bedingung war bei unseren linearen Problemen in den vorherigen Beiträgen nicht gegeben. Um solche Probleme zu lösen, verwendet man sogenannte Branch and Bound Verfahren.
Branch and Bound – ein Beispiel
Wir haben hier wieder ein Optimierungsproblem mit der zusätzlichen Restriktion, dass 
und 
ganzzahlig sein müssen. In dem Koordinatensystem haben wir dir die Nebenbedingungen eingetragen und die zulässige Menge markiert: Sie wird durch das Branch and Bound Verfahren immer weiter auf diese möglichen ganzzahligen Punkte beschränkt und stoppt, sobald es den Punkt gefunden hat, der das beste Ergebnis darstellt.
Branch and Bound: Erster Schritt
Als erstes musst du die optimale Lösung des Problems ermitteln, falls diese nicht schon vorgegeben ist. Normalerweise kannst du sie einfach durch einsetzen und auflösen der Variablen berechnen. In diesem Beispiel ist das Optimierungsproblem:
Als Nebenbedingung sind gegeben:
Die Rechenschritte dazu sind:
- Gleichung II verdoppeln und nach auflösen:
- In Gleichung I einsetzen
- Dann nach auflösen
- In Gleichung II einsetzen
- nach x_1 auflösen
Die Lösung zu unserem Optimierungsproblem lautet (2.14; 1.143)
Wie du siehst, sind das keine ganzen Zahlen. Eingesetzt in die Zielfunktion ergibt das 7,57. Das ist jetzt die obere Schranke deiner Zielfunktion. Das bedeutet: Die 7,57 ist vorübergehend unser optimales Ergebnis, bis wir unseren neuen Zielfunktionswert bestimmt haben.
Als nächstes definierst du deine untere Schranke. Wenn diese nicht bereits vorgegeben ist, fangen wir mit (0;0) an. Von hier verzweigen wir das Problem 
in zwei weitere Teilprobleme. Das nennt man branching. Im ersten Schritt subtrahierst du die optimale Lösung von der nächstgrößeren ganzen Zahl. Wir erhalten: 3- 2,14 = 0,86 und 2-1,143= 0,857.
Verzweigen nach der LIFO-Regel
Die Zahl mit der größeren Differenz gibt unsere erste Verzweigung an. Für die erste Variable gibt es nun zwei Möglichkeiten: Der rechte Ast beschreibt den Fall, dass größer gleich 3 ist und der linke Ast, dass kleiner gleich 2 ist. Das nennt man bounding. Wir machen zwei Kreise für beide Teilprobleme. Da wir das linke zuletzt gezeichnet haben, fangen mit dem linken Teilproblem an und schreiben in den Kreis 
. Diese Verzweigungsregel ist die Last In First Out oder auch LIFO-Regel. Das bedeutet: Wir verzweigen immer nach dem Teilproblem als erstes, das wir als letztes hinzugefügt haben.
Zielfunktion erneut berechnen
Jetzt berechnest du die Zielfunktion erneut – allerdings mit dem neuen Wert von gleich 2. In unserem Koordinatensystem siehst du wie die zulässige Menge weiter beschränkt. Unser müssen wir jetzt an die neue Einschränkung anpassen. Du findest es über den Schnittpunkt von mit einer Nebenbedingung. Wichtig ist, dass dieser immer innerhalb der zulässigen Wertemenge liegt. In unserem Fall ist das der Schnittpunkt mit der blauen Nebenbedingung.
Gleichgesetzt und aufgelöst nach erhältst du damit 1,2. Setzt du das in die Zielfunktion F ein, ergibt das 7,2. Da noch nicht ganzzahlig ist, müssen wir weiter verzweigen.
Neue Verzweigung durchführen
Wir teilen wieder in zwei Teilprobleme auf und verzweigen nach größer gleich 2 und kleiner gleich 1.
Wir beginnen wieder links aufgrund der LIFO-Regel. Unser 
ist jetzt (2;1), da beide Restriktionen der Teilprobleme und gelten. Der Zielfunktionswert für 
ist damit 7. Das ist jetzt auch gleichzeitig unsere neue untere Schranke, da eine zulässige Lösung mit ganzzahligen Variablen und kleiner als 7,57 ist. Das heißt: Schlechter als 7 darf unsere Zielfunktion in den anderen Teilproblemen nicht mehr werden.
Rechtes Teilproblem lösen
Da wir für dieses Ergebnis eine zulässige Lösung gefunden haben, gehen wir zum rechten Teilproblem von weiter und benennen es 
. Hier soll unser größer gleich 2 sein. Wenn du einen Blick auf das Koordinatensystem wirfst, siehst du sofort, dass das nicht möglich ist, da es durch unser außerhalb des zulässigen Bereichs liegt.
Ergebnisfindung:
Damit können wir zur ersten Verzweigungsebene zurückkehren. Den offenen Zweig benennen wir mit der nächsten Zahl, also 
. Für die Berechnung von setzen wir die rote Nebenbedingung wieder mit unserem Zweig, also der Restriktion eins größer gleich 3, gleich und erhalten gleich null. Der Zielfunktionswert für ist damit 9. Du siehst bestimmt schon, dass wir hier nicht mehr weiter verzweigen können und die bestmögliche Lösung gefunden haben.
Oftmals findet man diese schon bei einem der früheren Teilproblemen und muss dann überprüfen, ob es noch bessere Lösungen gibt. Manchmal kommst du sogar durch Ausprobieren schneller auf die Lösung. Bei zunehmender Anzahl der Variablen steigen die möglichen Lösungen aber exponentiell und es ist dann nicht mehr so einfach zu lösen.
Branch and Bound II
Im ersten Teil des Beitrags haben wir dir bereits gezeigt, wie man ein kombinatorisches ganzzahliges Problem lösen kann. In diesem Beitrag betrachten wir ein binäres kombinatorisches ganzzahliges Problem.
Branch and Bound – ein Beispiel
Stell dir vor, du willst deinen Koffer für den Urlaub packen und hast eine Auswahl an Sachen, die du gerne mitnehmen möchtest. Jeder Gegenstand hat ein bestimmtes Gewicht und einen bestimmten Nutzen für dich. Dein Koffer darf für den Flug aber nicht schwerer als 15 Kilogramm sein. Jetzt willst du den Koffer optimal packen und dabei das maximal zulässige Gewicht einhalten. Da du ja nur ganze Gegenstände und nicht nur einen Bruchteil mitnehmen kannst, musst du entscheiden, ob du den Gegenstand einpackst oder zu Hause lässt
Erklärung der Voraussetzungen
Das Problem sieht also folgendermaßen aus: Du siehst in der Zielfunktion deine Gegenstände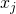 
gleich 1 bis 3, die du einpacken kannst, multipliziert mit ihrem jeweiligen Nutzen für dich. Du hast zwei Nebenbedingungen. Die erste zeigt die Gewichte der jeweiligen Gegenstände in Kilogramm und soll zusammenaddiert weniger oder gleich 15 Kilogramm wiegen. Die zweite Nebenbedingung sagt, dass jeder Gegenstand 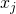nur Element der Zahlen 0 oder 1 sein kann, also eine binäre Variable ist. Null steht dafür, dass der Gegenstand nicht eingepackt wird und 1, dass er eingepackt wird. Um gleich im Branch and Bound Verfahren bestimmen zu können, nach welcher Variable verzweigt werden soll, musst du eine Priorität der Sachen festlegen. Diese bestimmt sich durch den relativen Nutzen. Dieser setzt sich zusammen aus dem Nutzen des jeweiligen Gegenstandes geteilt durch sein Gewicht. Die Prioritäten sehen damit so aus:
Branch and Bound Methode durchführen
Jetzt können wir das Branch and Bound Verfahren starten. Unsere untere Schranke ist 0. Unsere obere Schranke ist die nach Priorität hinzugefügten Gegenstände bis der Koffer voll ist. ist damit 1 und wir haben schon 4kg in unserem Koffer. Die zweithöchste Priorität hat Gegenstand und wiegt 5 kg. Zusammen mit sind das schon 9 kg. Als nächstes ist 
dran, der 10 kg wiegt. Das passt jetzt aber nicht mehr komplett in unseren Koffer, da wir dann bei 19 kg wären. Deshalb nehmen wir von nur 6/10 in x auf und haben damit genau 15 kg erreicht. Unsere Zielfunktion ist dann: 8+6+6/10*10=20. Wir haben damit unsere obere Schranke ermittelt.
Verzweigen nach der MUB-Regel
Diesmal verzweigen wir nach der Maximum Upper Bound- oder auch MUB-Regel. Das bedeutet: Anders als bei der LIFO-Regel berechnen wir direkt die Schranken aller Teilprobleme. Ausgehend von verzweigen wir jetzt nach abfallender Priorität – also zuerst . Links verzweigen wir nach gleich 1 und benennen das Teilproblem und rechts nach gleich 0 und nennen es . Wir starten mit und berechnen . Dadurch, dass in bereits 1 ist, ändert sich an sowie an der Zielfunktion nichts.
Da wir die MUB-Regel verwenden, teilen wir jetzt nicht auf, sondern berechnen erst . Hier soll gleich 0 sein. Demnach nehmen wir und auf und kommen auf genau 15 kg. Das ist unsere erste zulässige Lösung. Wir berechnen unsere Nutzenzielfunktion und kommen auf einen Nutzen von 16. Das ist jetzt unsere untere Schranke. Unser Nutzen darf also nicht weniger als 16 in den folgenden Teilproblemen betragen. Jetzt verzweigen wir weiter und zwar nach dem Gegenstand mit der nächsten Priorität nach – also . Für 
gilt gleich 1. Dabei verändert sich an den Gegenständen, die wir einpacken, und an der Zielfunktion wieder nichts.
Für ist das allerdings anders. ist hier 0 und es gilt die Bedingung von vorher, dass gleich 1 ist. Dadurch erhalten wir diese Kombination:
Ergebnisfindung:
Der Zielfunktionswert ist 18. Nach der MUB-Regel machen wir jetzt mit dem Teilproblem weiter, das die höhere obere Schranke hat, also 
. erhält gleich 1 und ist damit unzulässig, da die 15 Kilogramm bei dieser Option überschritten werden. Für 
muss gleich 0, gleich 1 und 
gleich 1 sein und wir erhalten einen Zielfunktionswert von 14.
Wir müssten an dieser Stelle noch weiter verzweigen. Da der Zielfunktionswert aber schon niedriger ist als unsere höchste obere Schranke, können wir an dieser Stelle abbrechen. Unser maximaler Nutzen ist demnach 18. Für dich ist es also am besten, wenn du die Uhr und deine Schuhe einpackst.
Du siehst: Es kommt immer ganz auf das Beispiel an, ob man eher die LIFO- oder die MUB-Regel verwenden sollte.