Tourenplanung – Savings-Verfahren
Du fragst dich was man unter dem Savings-Verfahren in der Tourenplanung versteht? Perfekt, denn genau das erklären wir dir in diesem Beitrag.
Inhaltsübersicht
Vorabüberlegung zur Transportplanung
Deine fertig produzierten Waren stehen abholbereit in deinem Lager und jetzt fragst du dich, was nun? In diesem Video zeigen wir dir wie du die Ware am besten an den Mann bringen kannst.
Wie du weißt besteht eine Supply Chain immer aus Beschaffung, Produktion, Distribution und Absatz. Zur Distribution zählt auch die Transportplanung. Ein wichtiger Bestandteil davon ist die Tourenplanung. Schließlich musst du ja auch planen, wie deine Ware zum Kunden gelangt. In unserem Beispiel liefern wir Brillen zu verschiedenen Optikern.
Erst mal musst du dich entscheiden, ob du auf Fremdtransporte zurückgreifen oder lieber deine eigenen Fahrzeuge aussenden willst. Unser Fokus liegt auf deinen eigenen Fahrzeugen, denn nur hier musst du die Tourenplanung selbst übernehmen.
Traveling Salesman-Problem und Chinese Postman-Problem
Es gibt grundsätzlich zwei verschiedene Arten von Problemen. Das Traveling Salesman-Problem(TSP) und das Chinese Postman-Problem(CPP). Beim TSP wird die Reihenfolge von Orten in einer Tour zusammengefasst. Ein Vertreter oder ein Händler plant nach diesem Schema seine Routen. Beim CPP wird die Reihenfolge der Straßen in einer Tour zusammengefasst. Wie beispielsweise bei einem Postboten, der an einer Straße anhält und dann überall in dieser Reihe seine Pakete und Briefe abgibt.
Damit wir die Aufgaben der Tourenplanung besser verstehen, schauen wir uns zunächst mal das Grundproblem der Tourenplanung an. Unsere Tour wird immer im Lager gleich 0 starten und i=1, …, n (i gleich eins bis n Kunden) anfahren. Unsere Fahrzeuge haben eine Kapazität von Q Mengeneinheiten und unsere Kunden einen Bedarf von B i. Wir suchen nach den Touren, die unsere Fahrzeuge jeweils am besten abfahren sollten. Als Nebenbedingungen müssen wir alle Aufträge abdecken und die Fahrzeugkapazität pro Tour einhalten.
Unser Ziel ist es, die Gesamtstrecke, die Gesamtfahrtzeit, die variablen Kosten und die eingesetzten Fahrzeuge zu minimieren. Es entstehen dabei zwei Teilprobleme: Die Zuordnung der Kunden zu den Touren und die Reihenfolge der Kunden innerhalb einer Tour.
Die Problemstellung kann natürlich nochmal deutlich erweitert werden. Mit zunehmenden Beschränkungen, z.B. maximale Fahrtdauer und unterschiedliche Kosten pro Fahrzeug, nimmt auch die Komplexität deiner Planung zu.
Das Savings-Verfahren
Grundsätzlich sind bei der Tourenplanung zwei verschiedene Verfahren zu unterscheiden, mit denen wir die optimale Tour ermittelt können: Das Savings-Verfahren und das Sweep-Verfahren. Schauen wir uns ersteres einmal genauer an:
Das einstufige Savingsverfahren ist ein heuristisches Eröffnungsverfahren. Trotz seiner simplen Herangehensweise lässt es sich sehr gut auf komplexere Problemstellungen übertragen.
Dabei werden die beiden Teilprobleme gleichzeitig, also simultan, gelöst. Wir integrieren dabei sukzessiv, also nacheinander, weitere Kunden in die Tourenpläne. Ausgangspunkt unserer Savingsberechnungen sind dabei immer Pendeltouren vom Lager zu den einzelnen Kunden. Die Strecke der Pendeltour ergibt sich jeweils durch die Entfernung vom Kunden zum Lager mal 2. Die Einsparungen für ein Kundenpaar, das zusammen statt in einzelnen Pendeltouren angefahren wird, nennt man Savings. Dein Ziel ist es natürlich, die Savings zu maximieren.
Schritt 1: Ermittlung der Savings
Schauen wir uns das an einem Beispiel an. Die Zahlen IN den Kästen, also in unserem Fall den Optikern, beschreiben jeweils die Kundennummer i. Die Nummern ÜBER den Kästen jeweils den Bedarf an Mengeneinheiten des Kunden b i. Die Beschriftung der Linien beschreibt die Längeneinheiten zwischen den Kunden i j, also die Länge der Fahrstrecke d i j ab. Unsere Fahrzeugkapazität Q ist gleich 10 Mengeneinheiten. Wir haben zusätzlich die jeweils kürzesten Wege zwischen den Kunden gegeben. Die Strecken sind in folgender Tabelle zusammengefasst.
Darauf aufbauend ermitteln wir die Savings, die wir erhalten, wenn wir zwei Kunden zusammen anfahren. Dafür benötigen wir folgende Formel:
Für die Streckenkombination Kunde 1 und Kunde 2 ergibt sich beispielsweise:
So kannst du für alle Streckenkombinationen die Savings berechnen. Am Ende kommst du dann auf folgende Tabelle:
Schritt 2: Kombination der Touren
Jetzt sortieren wir die berechneten Savings absteigend um zu sehen, welche Streckenkombination die höchsten Einsparungen erzielt. In unserem Beispiel trifft das auf die Kombination von Tour 2 und Tour 4 zu 
. Wir können die Pendeltouren T2 und T4 also streichen und berechnen stattdessen die Streckenlänge der kombinierten Tour 2,4.
Tipp für die Klausur
In der Klausur kannst du dir viel Zeit sparen, wenn du immer zu aller erst prüfst, ob du diese Touren überhaupt kombinieren kannst. Überprüfe hierfür einfach ob deine Fahrzeugkapazität ausreicht, um beide Kunden zusammen anzufahren. Ist dies nicht der Fall, machst du einfach ein großes X in die Spalte und gehst weiter zur nächsten Spalte. In unserem Fall sind die Bedarfe von Tour 2 und 4 kleiner gleich 10 ME. Wir können die Touren also kombinieren. Hierfür addieren wir zuerst die einzelnen Pendeltouren und ziehen von dieser Summe dann die entsprechenden Savings ab. Die dazugehörige Formel sieht so aus:
Um E T2 und E T4 zu berechnen, brauchen wir wieder die Formel:
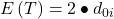
Mit dieser können wir leicht ausrechnen, dass:
Davon müssen wir jetzt nur noch die Savings abziehen:
Somit kommen wir auf eine Streckenlänge der Tour E von 44 Längeneinheiten:
Schritt 3: Tourenkombination mit einem weiteren Kunden
Als nächstes schauen wir uns an, welche Savings wir erhalten, wenn wir die neue Tour mit einem weiteren Kunden kombinieren. Vorher sollten wir aber wieder überprüfen, ob wir die jeweiligen Touren überhaupt kombinieren können, ohne dass dabei unsere Fahrzeugkapazität Q gleich 10 ME überschritten wird. Für die Tourenkombination 2,4,3 und 2,4,6 brauchst du die Savings beispielweise erst gar nicht berechnen, da hier der Kundenbedarf 11 ME bzw. 12 ME beträgt und somit unsere Fahrzeugkapazität übersteigt.
Bleiben also noch die Tourenkombinationen 2,4,1 und 2,4,5 für die Savingsberechnung. Die Tour 2,4,1 hat folgenden Bedarf: Kunde 2 und 4 haben gemeinsam einen Bedarf von 6 ME, Kunde 1 von 3 ME. Wir bleiben also unter 10 ME und können die Tour fahren.
Da wir jetzt die Savings mit einer bereits kombinierten Tour berechnen, benötigen wir jetzt folgende Formel:
Setzen wir unsere Werte ein, sieht das für die Savings von Tour 2,4,1 so aus:
Für die Savings von 2,4,5 sieht das ganze so aus:
Also:
Jetzt beginnt das Spiel wieder von vorne. Du schreibst also wieder die Savings in absteigender Reihenfolge auf, setzt die Tour ein, die die meisten Einsparungen erbringt und berechnest die Streckenlängen, die sich aus der neuen Kombinationen ergeben. Das funktioniert immer nach dem gleichen Schema.
Abhilfe durch graphische Darstellung
Wenn es dir schwer fällt, die Strecken in der Tabelle abzulesen, kannst du das auch anhand der Graphik machen.
Zum Beispiel ist die Strecke vom Lager zu Kunde 3 gleich 5 LE. Wenn du einen Kunden ohne direkte Verbindung anfährst, musst du natürlich aufpassen, dass du die kürzeste Strecke wählst und musst dann die Teilstrecken zusammenzählen. Um zu Kunde 4 zu gelangen ist der Weg über Kunde 3 und 2 beispielsweise deutlich kürzer als der Weg über Kunde 5.
Die Savings für die Tour Lager-Kunde 1-Kunde 2- Lager berechnest du zum Beispiel, indem du die einzelnen Pendelstrecken addierst, also:
und davon die Summe aus 13 LE, 12 LE und 8 LE abziehst, damit du keine Strecke doppelt berechnest.
Ob Tabelle oder Graphik – suche dir am besten die Variante aus, die für dich einfacher und vor allem schneller ist.
Das war´s auch schon vom Savingsverfahren. Jetzt kannst du dich beruhigt um die Transportplanung in deiner Firma kümmern.