Video

Quiz

Gleichförmige Bewegung

Wichtige Inhalte in diesem Video

Was ist eine gleichförmige Bewegung?

Gleichförmige Bewegung Formel

Vektorielle Darstellung

Weg-Zeit-Gesetz:

Geschwindigkeits-Zeit-Gesetz:

Beschleunigungs-Zeit-Gesetz:

Gleichförmige Bewegung Aufgaben

Du fragst dich was eine gleichförmige Bewegung ist und was genau gleichförmig bedeutet? Dann bist du hier genau richtig. Wir zeigen dir was es damit auf sich hat und wie man sie schnell und einfach berechnet.

Schau auf jeden Fall noch das Video zum Artikel an. Das ist nicht nur spannend sondern zeigt dir auch alle relevanten Inhalte audiovisuell aufbereitet.

Inhaltsübersicht

Was ist eine gleichförmige Bewegung?

im Videozur Stelle im Video springen

Eine gleichförmige Bewegung ist eine geradlinige Bewegung. Das heißt ein Objekt bewegt sich gleichbleibend entlang einer geraden Linie. Die Geschwindigkeit ist dabei konstant und die Beschleunigung, beziehungsweise Entschleunigung, Null. Das heißt es wirkt keine äußere Kraft auf das Objekt, weswegen auch dessen Richtung unverändert bleibt. Betrachtest du etwas, dass vollkommen still steht, handelt es sich im Grunde um eine gleichförmige Bewegung mit der Geschwindigkeit Null.

Ein gutes Beispiel sind hierbei Asteroiden. Diese bewegen sich mit konstanter Geschwindigkeit durchs Vakuum des Weltalls. So lange sie nicht von einer Sonne oder einem Planeten eingefangen werden, haben diese Asteroiden auch keine Beschleunigung. Fliegt so ein Gesteins- oder Eisbrocken durchs All bewegt er sich immer gerade aus mit immer der gleichen Geschwindigkeit.

Definition gleichförmige Bewegung

Ein Objekt bewegt sich gleichförmig, wenn dessen Geschwindigkeit konstant und seine Beschleunigung Null ist.

Gleichförmige Bewegung Formel

im Videozur Stelle im Video springen

In der Physik betrachtest du solche Probleme mithilfe der Mathematik und Formeln. Das bedeutet im Fall der gleichförmigen Bewegung, dass du eine Formel brauchst, welche die Strecke s, Geschwindigkeit v, Zeit t und den Anfangsweg s₀ in Relation zueinander setzt.

Die zurückgelegte Strecke s ist nämlich das Produkt aus der Geschwindigkeit v des Objektes und der vergangene Zeit t. Den Anfangswert s₀ brauchst du, wenn deine Messung ab einem bestimmten Punkt innerhalb der Strecke beginnt, dein Objekt sich vor deiner Messung aber bereits um eine gewissen Strecke bewegt hat.

s = v • t + s₀

In den meisten Problemen, welche du berechnen wirst, ist der Anfangsweg nicht wichtig. Dadurch reduziert sich die Formel auf:

s = v • t

Die Einheit der Strecke ist der Meter (m). Die Einheit der Zeit gibst du in Sekunde (s) oder auch Stunde (h) an. Du siehst aber anhand der Formel, dass die Geschwindigkeit auch mit einfließt. Aus dem Alltag ist dir vielleicht bekannt, dass Geschwindigkeiten in Kilometer pro Stunde (km/h) angegeben werden. In der Physik allerdings gibst du Geschwindigkeit mit der Einheit Meter pro Sekunde an (m/s).

Die Umrechnung ist aber ganz einfach. Als Beispiel nehmen wir eine Geschwindigkeit von 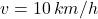$v = 10 \, km/h$ an und rechnen diese in m/s um und anschließend $v = 10 \, m/s$ und rechnen diese in km/h um.

$v = 10 \, km/h = 10 \cdot \frac{1000 \, m}{3600 \, s} = \frac{10}{3,6} \frac{m}{s} = 2,78 \, m/s$

$v = 10 \, m/s = 10 \cdot \frac{\frac{1}{1000} \, km}{\frac{1}{3600} \, h} = 10 \cdot \frac{3600}{1000} \frac{km}{h} = 10 \cdot 3,6 \, km/h = 36 \, km/h$

Du siehst eine Geschwindigkeit von 10 m/s entspricht also 36 km/h, während eine Geschwindigkeit von 10 km/h einer Geschwindigkeit von 2,78 m/s entspricht. In beiden Fällen taucht der Faktor 3,6 auf.

Merke Einheitenumrechnung

Rechnest du km/h in m/s um teilst du deine Geschwindigkeit durch 3,6.
Rechnest du m/s in km/h um multiplizierst du deine Geschwindigkeit mit 3,6.

Vektorielle Darstellung

im Videozur Stelle im Video springen

Die meisten Bewegungen finden in drei Dimensionen statt, also in den drei Raumrichtungen (oben/unten, links/rechts, vor/zurück). Daher nutzt du für die allgemeine Darstellung dieser Zusammenhänge die Vektordarstellung. Das bezeichnest du auch als Gesetze.

Weg-Zeit-Gesetz:

im Videozur Stelle im Video springen

Das Weg-Zeit-Gesetz ist die vektorielle Darstellung der dir schon bekannten Formel. Sie setzt den Weg s und die Geschwindigkeit v zueinander in Relation.

$\vec{r}(t) = \vec{v}_0 \cdot t + \vec{r}_0$

Geschwindigkeits-Zeit-Gesetz:

im Videozur Stelle im Video springen

Die Geschwindigkeit ist die erste Ableitung des Weges nach der Zeit. Bei der gleichförmigen Bewegung haben wir diese Geschwindigkeit bereits als konstant definiert.

$\dot{\vec{r}}(t) = \vec{v}(t) = v_0 = konst.$

Beschleunigungs-Zeit-Gesetz:

im Videozur Stelle im Video springen

Die Beschleunigung ist die zweite Ableitung des Weges nach der Zeit. Da die Geschwindigkeit konstant ist, muss deine Beschleunigung Null sein. Dein Körper wird also weder langsamer noch schneller. Dementsprechend ist die Beschleunigung a=0 .

$\ddot{\vec{r}}(t) = \vec{a}(t) = \vec{a} = 0$

In diesen Formeln stehen $\vec{r}_0$ für den Ortsvektor zum Zeitpunkt Null, $\vec{v}_0$ für den konstanten Geschwindigkeitsvektor, $\vec{a}$ für den Beschleunigungsvektor und für die Zeit.

Geschwindigkeit Zeit Diagramm Gleichförmige Bewegung

Bei der gleichförmigen Bewegung gilt, für die im Zeitraum $\Delta t$ zurückgelegte Strecke $\Delta s$ : Die Geschwindigkeit $v = \frac{\Delta s}{\Delta t}$ ist konstant. Das bedeutet, dass in gleichen Zeitintervallen gleiche Wegstrecken zurückgelegt werden.Der Weg ist also proportional zur Zeit: $\Delta s \~ \Delta t$ . $\Delta t$ beschreibt hierbei einen Zeitunterschied (Zeitdifferenz) und keinen genauen Zeitpunkt. Du berechnest die Strecke über $\Delta s = v \cdot \Delta t$ .

Das alles kannst du auch grafisch Darstellen.

Beginnen wir mit dem Weg-Zeit-Diagramm. Auf der x-Achse trägst du die Zeit und auf der y-Achse die Strecke auf. Der Zeitraum t_1 - 0 hat die gleiche Länge wie t_3 - t_2 . Die Strecke s_1 - 0 hat die gleiche Länge wie s_3 - s_2 . Trägst du die Punkte entsprechend in den Graph ein, siehst du einen linearen Anstieg. Bei konstanter Geschwindigkeit nimmt auch unsere zurückgelegte Strecke konstant zu.

Weg-Zeit-Diagramm, Gleichförmige Bewegung, geradlinige Bewegung, gleichförmige geradlinige Bewegung, Geschwindigkeit, Beschleunigung — Gleichförmige Bewegung s-t-Diagramm.

Als nächstes kommen wir zum Geschwindigkeit-Zeit-Diagramm. Auf der x-Achse steht die Zeit und auf der y-Achse die Geschwindigkeit. Da die Geschwindigkeit konstant ist, siehst du eine einfache horizontale, gerade Linie.

Geschwindigkeits-Zeit-Diagramm, Gleichförmige Bewegung, geradlinige Bewegung, gleichförmige geradlinige Bewegung, Geschwindigkeit, Beschleunigung — Gleichförmige Bewegung v-t-Diagramm (mit Zahlen von vorherigem Bild).

Zuletzt schauen wir uns das Beschleunigungs-Zeit-Diagramm an. Auf der x-Achse steht hier wieder die Zeit und auf der y-Achse die Beschleunigung. Da die Geschwindigkeit konstant ist und sich nicht ändert, ist die Beschleunigung Null. Daher verläuft die Beschleunigungskurve genau auf der x-Achse am Wert 0.

Beschleunigungs-Zeit-Diagramm, Gleichförmige Bewegung, geradlinige Bewegung, gleichförmige geradlinige Bewegung, Geschwindigkeit, Beschleunigung — Gleichförmige Bewegung a-t-Diagramm.

Quiz zum Thema Gleichförmige Bewegung

Gleichförmige Bewegung Aufgaben

im Videozur Stelle im Video springen

Zum Abschluss lernst du anhand von zwei Beispielen wie man die Formeln zur Beschreibung verschiedener Probleme benutzt.

Als erstes stell dir vor, dass du am Joggen bist. Deine Geschwindigkeit beträgt $v = 2 \, \frac{m}{s}$ . Du läufst an einem Baum vorbei und stoppst die Zeit bis zum nächsten. Du misst eine Zeitspanne von $t = 5 \, s$ . Wie weit bist du gelaufen?

$s = v \cdot t + s_0 = 2 \, m/s \cdot 5 \, s + 0 \, m = 10 \, m$

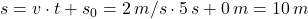
In fünf Sekunden bist du also 10 m gelaufen.

Als nächstes stellt dir vor, du bist $s = 75 \, m$ zum Bäcker gelaufen. Für die Strecke hast du $t = 25 \, s$ gebraucht. Wie schnell bist du gelaufen?

$v = \frac{s}{t} = \frac{70 \, m}{25 \, s} = 3 \frac{m}{s}$

Du bist also mit drei Metern pro Sekunde zum Bäcker gelaufen.

zur Videoseite: Gleichförmige Bewegung

Beliebte Inhalte aus dem Bereich Dynamik

Bewegung in der Physik

Gleichförmige Bewegung

Gleichmäßig beschleunigte Bewegung

Bewegungsgleichungen

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .