Video

Quiz

Hier geht's zum Video „Geschwindigkeit berechnen“

Hier geht's zum Video „Beschleunigung berechnen“

Hier geht's zum Video „Schiefer Wurf“

Waagerechter Wurf

Wichtige Inhalte in diesem Video

Waagerechter Wurf einfach erklärt

Waagerechter Wurf Formel

Zeit-Geschwindigkeit-Gesetz

Weg-Zeit-Gesetz

Waagerechter Wurf Aufgaben

Wie ein waagerechter Wurf definiert ist und du herausfindest, wie schnell sich das geworfene Objekt bewegt oder wie weit es fliegt erfährst du in diesem Artikel.

In unserem Video erklären wir dir alle nötigen Informationen zum waagerechten Wurf, die du zur Ermittlung unterschiedlichster Fälle benötigst.

Inhaltsübersicht

Waagerechter Wurf einfach erklärt

im Videozur Stelle im Video springen

Der waagerechte Wurf, oder auch horizontaler Wurf ist die Bewegung eines Körpers, der parallel zum Horizont geworfen oder geschossen wird. Betrachtet man die Bahnkurve des waagerecht geworfenen Körpers, handelt es sich um eine Parabel, bei welcher der Scheitelpunkt den Abwurfort repräsentiert. Das bedeutet wiederum, dass der Körper zwei unterschiedliche Bewegungsformen durchführt.

Waagerechter Wurf Formel

im Videozur Stelle im Video springen

Wie sich nun ein waagerechter Wurf berechnen lässt, schauen wir uns im Folgenden anhand eines konkreten Beispiels an.

Angenommen du stehst auf einem Hochhaus und schießt einen Fußball parallel zum Horizont über die Kante des Hochhauses. Dann beschreibt die Flugbahn des Balls einen waagerechten Wurf.

Beispielfall und Flugbahn mit jeweiligen Geschwindigkeitskomponenten, Waagerechter Wurf mit Ball von Haus aus — Beispielfall und Flugbahn mit jeweiligen Geschwindigkeitskomponenten

Je nachdem, welche Informationen gegeben sind, lassen sich beim waagerechten Wurf unterschiedliche Komponenten ermitteln.

Bevor wir die konkreten Formeln aufstellen können, muss die Gesamtgeschwindigkeit v_0 in die jeweiligen Geschwindigkeitskomponenten für die – und -Richtung zerlegt werden. Der Ball führt innerhalb des Fluges nämlich zwei unterschiedliche Bewegungen aus.

In x-Richtung, also die Richtung in der sich der Ball vom Hochhaus entfernt, führt dieser eine gleichförmige Bewegung durch. Die Besonderheit besteht darin, dass die Anfangsgeschwindigkeit in -Richtung den Flug über konstant bleibt ( v_0=v_0_,_x ).

In y-Richtung handelt es sich um eine gleichmäßig beschleunigte Bewegung , da der Ball eine Abwärtsbewegung durchführt. Das bedeutet, dass der Ball wird immer schneller, je näher er dem Boden kommt ( $v_y=-g\cdot t$ ).

Zu beachten sind die Zusammenhänge bezüglich der Beschleunigung, Geschwindigkeit und dem Weg. Es gilt nämlich der Zusammenhang

a(t)=v'(t)=s''(t) ,

wobei hier den Weg, die Geschwindigkeit und die Beschleunigung darstellt. Mittels Integration können diese Schritte gleichermaßen rückwärts durchgeführt werden.

Betrachten wir nun die unterschiedlichen Bewegungen in Abhängigkeit von der Zeit, die der Ball sich in der Luft befindet.

Zeit-Geschwindigkeit-Gesetz

im Videozur Stelle im Video springen

Zum einen können Geschwindigkeitsfunktionen in Abhängigkeiten der Zeit in die jeweiligen Richtungen v_x(t) und v_y(t) aufgestellt werden.

Betrachten wir zunächst die Geschwindigkeit in -Richtung.

Wie schon beschrieben, führt der Ball in der -Komponente eine gleichförmige Bewegung aus. Das bedeutet, dass sich der Ball bei idealen Verhältnissen, also ohne Gegen-oder Rückenwind und unter Vernachlässigung der Luftreibung, innerhalb des Falls kontinuierlich vom Hochhaus entfernt. Dementsprechend ist die Geschwindigkeit in -Richtung zu jeder Zeit in der Luft gleich der Anfangsgeschwindigkeit.

Nach der Integration folgt zur Bestimmung der Geschwindigkeit in -Richtung:

$v_x(t)=a\cdot(t-t_0)+v_0_,_x$

Da der Körper keine Beschleunigung in x-Richtung erfährt und wir von idealen Verhältnissen ausgehen, ist die Beschleunigung in diesem Fall gleich null und es folgt:

v_0=v_0_,_x

daraus folgt für die Funktion in -Richtung (Zeitunabhängig da konstant):

Zeit-Geschwindigkeit Diagramm, Zeit, Geschwindigkeit, x-Richtung, konstant — Zeit-Geschwindigkeit Diagramm mit der Geschwindigkeit eines Körpers in x-Richtung

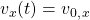
Schauen wir uns nun die Geschwindigkeit der -Komponente an.

Bei der -Komponente handelt es sich um eine gleichmäßig beschleunigte Bewegung ( $a=\mathrm{konst}$ .). Das wiederum heißt, dass der Ball immer schneller wird, je näher er dem Boden kommt. Das ist auf die Erdbeschleunigung , bzw. einer vom Koordinatensystem ausgehend negativen Beschleunigung , zurückzuführen.

$a=g=9,81\frac{\text{m}}{\text{s}^2}$

Wie schon in -Richtung erhält man durch Integration:

$v_y(t)=-a_0\cdot\left(t-t_0\right)+v_0_,_y$

Wobei v_0_,_y die Anfangsgeschwindigkeit in y-Richtung ist und t_0 ist die Zeit beim Abwurf, oder im Falle unseres Beispiels, beim Abschuss. Beim waagerechten Wurf ist diese Anfangsgeschwindigkeit v_0_,_y in y-Richtung gleich Null. Darauf folgt:

$v_y(t)=-g\cdot t$

Zeit-Geschwindigkeit Diagramm, Zeit, Geschwindigkeit, y-Richtung, waagerechter Wurf — Zeit-Geschwindigkeit Diagramm mit der Geschwindigkeit eines Körpers in y-Richtung

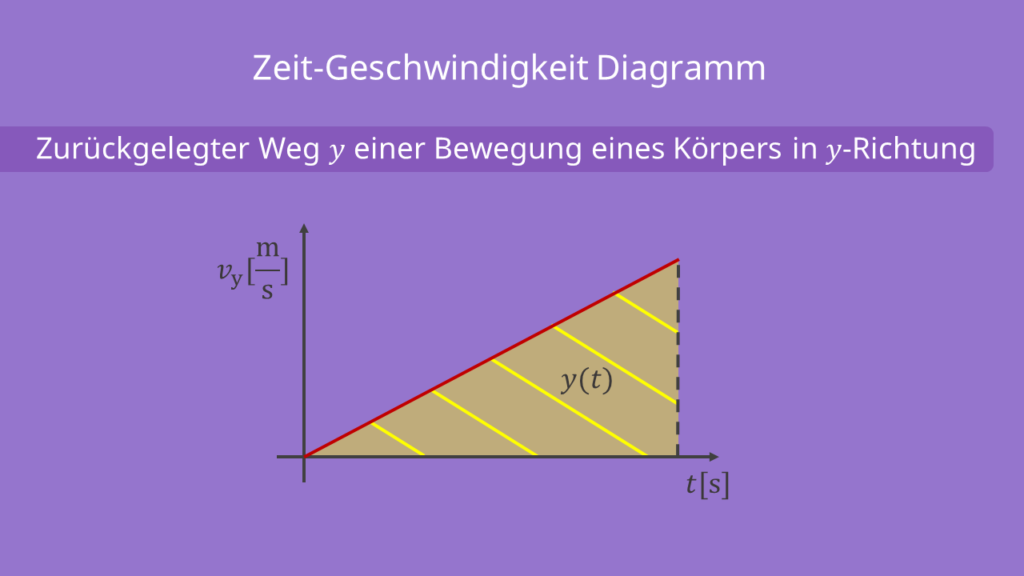
Weg-Zeit-Gesetz

im Videozur Stelle im Video springen

Um eine Aussage über die zurückgelegten Wege treffen zu können, werden in diesem Schritt die Wegfunktionen über die Zeit aufgestellt. Diese sind für die jeweiligen Richtungen dementsprechend y(t) und x(t) .

Wie schon beim Zeit-Geschwindigkeit Gesetzt betrachten wir zunächst die -Komponente.

Aufgrund der gleichförmigen Bewegung in -Richtung steigt die Entfernung mit der Zeit, die sich der Ball in der Luft befindet. Er entfernt sich also immer weiter vom Hochhaus. Mathematisch gesehen handelt es sich dabei um die Fläche unter der konstanten Geschwindigkeit. Die Geschwindigkeit ist die Ableitung des Weges nach der Zeit.

$v_0_,_x=\frac{\text{d}x}{\text{d}t}$

Demnach ist das Integral des Weges in -Richtung nach dem Weg, gleich dem Integral der Geschwindigkeit in -Richtung nach der Zeit.

Durch die Integration erhält man die Funktion:

$x=x_0+v_0_,_x\cdot\left(t-t_0\right)$

Bei x_0 handelt es sich um den Startpunkt auf der -Achse. Idealerweise beginnt man das Koordinatensystem auf Höhe des Aufprallortes und des Balls. Damit wäre x_0 und der Abwurfzeitpunkt t_0 gleich Null.

$x(t)=v_0_,_x\cdot t$

Zeit-Geschwindigkeit Diagramm, zurückgelegter Weg, waagerechter Wurf — Zeit-Geschwindigkeit Diagramm mit dem zurückgelegten Weg eines Körpers in x-Richtung

Schauen wir uns jetzt das gleiche für die -Richtung an.

Zur Beschreibung des Weges der -Komponente, also wie weit der Ball nach unten gefallen ist, muss beachtet werden, dass der Ball eine Abwärtsbewegung durchführt.

Der Weg in -Richtung kann bestimmt werden, indem das Integral des Weges in y-Richtung nach dem Weg, mit dem Integral der Geschwindigkeit über die Zeit gleichgesetzt wird.

$\int_{y_0}^{y}\mathrm{d}y=\int_{t_0}^{t}\!v_y\mathrm{d}t$

Setzt man nun die vorher ermittelte Geschwindigkeit $v_y=v_0_,_y+a_0\cdot\left(t-t_0\right)$ in das Integral ein folgt:

$\int_{y_0}^{y}\mathrm{d}y=\int_{t_0}^{t}\!\left(v_0_,_y+a_0\left(t-t_0\right)\right)\mathrm{d}t$

Aufgelöst ergibt sich:

$y-y_0=\frac{1}{2}\cdot a_0\left(t-t_0)^2+v_0_,_y\cdot \left(t-t_0\right)$

nach umgestellt folgt demnach:

$y=\frac{1}{2}\cdot a_0\left(t-t_0)^2+v_0_,_y\cdot \left(t-t_0\right)+y_0$

Die Funktion lautet also:

$y(t)=-\frac{1}{2}\cdot a_0\left(t-t_0\right)^2+v_0_,_y\cdot \left(t-t_0\right)+y_0$

Die sich hierbei ergebene Integrationskonstante y_0 beschreibt die Höhe des Abschussortes und es gilt:

y_0=h_0

Wobei x_0 hier den Abschussort in -Richtung darstellt, t_0 den Anfangszeitpunkt und v_0_,_y die Anfangsgeschwindigkeit in -Richtung. Wird demnach für die genannten Komponenten Null eingesetzt, ergibt sich die Zeit-Weg Gleichung:

$y(t)=-\frac{1}{2}\cdot a_0 \cdot t^2+h_0=-\frac{1}{2}\cdot g \cdot t^2+h_0$

Zeit-Geschwindigkeit Diagramm, waagerechter Wurf, zurückgelegter Weg — Zeit-Geschwindigkeit Diagramm mit dem zurückgelegten Weg in y-Richtung

Wurfparabel

im Videozur Stelle im Video springen

Möchte man wissen, in welcher Höhe sich der Ball während des Fluges befindet, muss man die x(t) und y(t) Gleichungen kombinieren. So kann zu jeder -Komponente, eine -Komponente zuordnet werden.

Die Bahngleichung y(x) , bei der zu jeder -Koordinate des Körpers, sich genau eine -Koordinate befindet, wird mithilfe der Funktion zur gleichförmigen Bewegung erstellt. Durch das Umstellen nach der Zeit und dem anschließenden einsetzen in die Formel der beschleunigten Bewegung in -Richtung, erhält man die Höhe nach dem Weg .

$x(t)=v_0_,_x\cdot t$

Nach der Zeit umgestellt demnach:

$t=\frac{x}{v_0_,_x}$

Setzt man nun die Variable in die y(t) Funktion ein, erhält man die Bahngleichung y(x) :

$y(x)=-\frac{1}{2}\cdot a_0\left(\frac{x}{v_0_,_x}\right)^2+v_0_,_y\cdot \left(\frac{x}{v_0_,_x}\right)+h_0$

Da die Abwurfgeschwindigkeit in -Richtung gleich null ist folgt:

$y(x)=-\frac{1}{2}\cdot a_0\left(\frac{x}{v_0_,_x}\right)^2+h_0$

Speziell beim horizontalen bzw. waagerechten Wurf, ist die Winkelkoordinate $\alpha$ der Anfangsgeschwindigkeit v_0 , gleich null. Wenn du mehr über den Abschuss mit einem Winkel, der ungleich 0 ist ( $\alpha\neq0$ ), wissen möchtest, schau dir doch unser Video zum schiefen Wurf an.

Waagerechter Wurf (α=0°) und Schiefer Wurf (α≠0°) — Waagerechter Wurf ( α = 0°) und Schiefer Wurf ( α ≠ 0°)

Wurfhöhe

im Videozur Stelle im Video springen

Die Wurfhöhe h_0 ist die Höhe, bei der sich der Ball zu der Zeit null befindet y(t=0) . Setzt man demnach für und v_0_,_y gleich null in die Funktion ein folgt:

$y(x)=-\frac{1}{2}\cdot a_0\left(\frac{0-0}{v_0_,_x}\right)^2+0\cdot \left(\frac{x-x_0}{v_0_,_x}\right)+y_0$

y(x=0)=y_0

y(x=0)=y_0=h_0

Setzt man die Funktion y(x) gleich null und für die Wurfweite x_w ein, erhält man die Wurfhöhe:

$y(x=x_w)=0=-\frac{1}{2}\cdot a_0\left(\frac{x_w-0}{v_0_,_x}\right)^2+0\cdot \left(\frac{x_w-x_0}{v_0_,_x}\right)+h_0$

$y(x=x_w)=0=-\frac{1}{2}\cdot a_0\left(\frac{x_w}{v_0_,_x}\right)^2+h_0$

$y(x=x_w)=h_0=\frac{1}{2}\cdot a_0\left(\frac{x_w}{v_0_,_x}\right)^2$

$h_0=\frac{1}{2}\cdot a_0\left(\frac{x_w}{v_0_,_x}\right)^2=\frac{1}{2}\cdot g\left(\frac{x_w}{v_0_,_x}\right)^2$

Wurfweite

im Videozur Stelle im Video springen

Die Wurfweite x_w ist die Weite, bei welcher der Ball auf dem Boden aufkommt. Die Wurfweite liegt also vor, wenn die Funktion y(x) gleich null wird oder man die Fallzeit in die Wegfunktion der -Richtung $x(t_F)=v_o\cdot t_F$ einsetzt.

Stellt man die vorher ermittelte Bahngleichung nach um und setzt für x_0=0 ein, erhält man die Wurfweite x_w :

$y(x)=0=-\frac{1}{2}\cdot a_0\left(\frac{x-0}{v_0_,_x}\right)^2+0\cdot \left(\frac{x-0}{v_0_,_x}\right)+h_0$

$y(x)=0=-\frac{1}{2}\cdot a_0\left(\frac{x-0}{v_0_,_x}\right)^2+h_0$

$\frac{1}{2}\cdot a_0\left(\frac{x_w-0}{v_0_,_x}\right)^2=h_0$

$x_w=v_0_,_x\cdot\sqrt{\frac{2\cdot h_0}{a_0}}}=v_0_,_x\cdot\sqrt{\frac{2\cdot h_0}{g}}}$

Fallzeit

im Videozur Stelle im Video springen

Die Zeit die der Ball benötigt, um auf dem Boden aufzukommen, wird Fallzeit t_F genannt.

Diese erhält man, indem die y(t) Funktion bei der höchsten Stelle der Parabel h_0 gleich null gesetzt wird:

$y(t)=-\frac{1}{2}\cdot a_0\left(t-t_0\right)^2+v_0_,_y\cdot \left(t-t_0\right)+y_0$

Die Funktion ist bei t_0=0 , v_0_,_y=0 , a=g und y_0=h_0 , folgt:

$y(t)=0=-\frac{1}{2}\cdot g \cdot t^2+h_0$

$t=t_F=\sqrt{\frac{2\cdot h_0}{g}}$

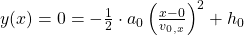
Waagerechter Wurf Aufgaben

im Videozur Stelle im Video springen

Du kennst jetzt alle notwendigen Formeln zur Berechnung von unterschiedlichen Aufgaben. Kommen wir nun zu einem interessanten Beispiel.

Stell dir vor, du stehst immer noch mit dem Fußball oben auf dem Haus. Du weißt, dass du den Ball mit einer Geschwindigkeit von 50 $\frac{\mathrm{km}}{\mathrm{h}}$ schießen kannst und und das Haus 15 Meter hoch ist.

Wie weit müsste sich dein Freund nun vom Haus hinstellen, damit er den Ball aus der Luft fangen kann? Für das einfachere Vorgehen, sind ideale Verhältnisse vorausgesetzt.

Beispielfall Haus - waagerechter Wurf Aufgabe Beispiel — Beispielfall Haus

In der Aufgabenstellung ist die Anfangsgeschwindigkeit v_0_,_x sowie die Höhe zum Zeitpunkt t gleich null y(t_F)=h_0 gegeben.

$v_0_,_x=50 \frac{\text{km}}{\text{h}}=13,88 \frac{\text{m}}{\text{s}}$

$h_0=15\mathrm{m}$

Gesucht ist nun die Wurfweite x_w .

Die Formel für die Wurfweite ergibt sich, wenn die Bahngleichung beim höchsten Punkt h_0 , gleich null wird:

$y(x)=0=-\frac{1}{2}\cdot a_0\left(\frac{x-x_0}{v_0_,_x}-t_0\right)^2+h_0$

Da wir den Bereich zwischen dem Aufkommen und dem Abschluss x_0 betrachten, ist x_0=0 , t_0=0 und es folgt nach dem Umstellen:

$x=x_w=v_0_,_x\cdot\sqrt{\frac{2\cdot h_0}{g}}$

Durch das Einsetzten der gegebenen Werte folgt:

$x_w=13,88\frac{\text{m}}{\text{s}}\cdot \sqrt{\frac{2 \cdot 15\text{m}}{9,81\frac{\text{m}}{\text{s}^2}}}$

Daraus Ergibt sich für die Wurfweite x_w :

$x_w=24,27\text{m}$

$x_w\approx 24\text{m}$

Dein Freund muss sich ca. 24 Meter vor dem Haus positionieren, um den Ball zu fangen.

Auf diese Art und Weise lassen sich durch Umstellen der Formeln alle Komponenten des waagerechten Wurfs ermitteln.

Quiz zum Thema Waagerechter Wurf

Schiefer Wurf

im Videozum Video springen

Neben dem waagerechten Wurf kannst du einen Körper auch „schräg nach oben und nach vorne“ werfen. Dabei handelt es sich um den sogenannten schiefen Wurf. Diesen kannst du, wie auch schon den waagerechten Wurf, mit mehreren Gesetzen und Wurfparabeln beschreiben.

Willst du mehr über den schiefen Wurf erfahren? Dann schau dir gerne unseren Beitrag dazu an!

Zum Video: Schiefer Wurf

zur Videoseite: Waagerechter Wurf

Beliebte Inhalte aus dem Bereich Dynamik

Waagerechter Wurf

Freier Fall Übungsaufgabe

Freier Fall Klausuraufgabe

Fallbeschleunigung

Senkrechter Wurf

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .