Schiefe Ebene
Die schiefe Ebene ist wohl eines der bekanntesten physikalischen Systeme überhaupt. Jeder von uns ist dem Prinzip der schiefen Ebene schon einmal begegnet, ob zum Heben von schweren Gegenständen oder beim Wandern im Gebirge. Hier erfährst du jetzt, wie solche schiefen Ebenen im Detail funktionieren.
Falls dir das Lernen audiovisuell unterstützt leichter fällt, schau dir unbedingt unser Video zur schiefen Ebene an!
Inhaltsübersicht
Schiefe Ebene einfach erklärt
Die schiefe Ebene, schräge Ebene oder auch geneigte Ebene ist ein physikalisches System aus der klassischen Mechanik und beschreibt eine ebene, zur Horizontalen geneigte Fläche, auf der sich eine Masse unter dem Einfluss ihrer Gewichtskraft (und der Reibung ) bewegt.
Dabei können wir die Gewichtskraft in einen Teil senkrecht zur schiefen Ebene (die Masse „drückt auf die Ebene“) und einen Anteil parallel zur Ebene (ihr Gewicht beschleunigt die Masse nach unten) zerlegen. Diesem zweiten Anteil wirkt die Reibungskraft entgegen. Je nach Stärke dieser Reibung kann die Bewegung der Masse auf der Ebene nach unten entweder beschleunigt sein oder mit konstanter Geschwindigkeit erfolgen. Die Masse kann also auch auf der schrägen Ebene ruhen.
Schauen wir im Folgenden die wirkenden Kräfte auf einer schiefen Ebene genauer an.
Schiefe Ebene Grundlagen
Beginnen wir unsere Diskussion der schiefen Ebene mit einem ihrer einfachen Spezialfälle, der waagrechten Ebene. Wir betrachten also eine Ebene mit Neigungswinkel 0 Grad zur Horizontalen und einen darauf liegenden Körper. Der Körper drückt jetzt mit seinem Gewicht auf die Ebene. Auf den Schwerpunkt
des Körpers (wir beschäftigen uns hier mit der Kinematik dieses Massepunkts
) wirkt also die Gewichtskraft  , die gerade nach unten und damit senkrecht zur Ebene wirkt.
, die gerade nach unten und damit senkrecht zur Ebene wirkt.
Die Ebene trägt die Masse und kompensiert daher  , indem sie die entgegen gerichtete Normalkraft
, indem sie die entgegen gerichtete Normalkraft  auf den Körper aufbringt. Im Gleichgewicht dieser beiden Kräfte
auf den Körper aufbringt. Im Gleichgewicht dieser beiden Kräfte  ruht der Körper.
ruht der Körper.
Jetzt neigen wir die Ebene um den Neigungswinkel  und erhalten die allgemeine, geneigte Ebene. In diesem Fall steht die Gewichtskraft nicht mehr senkrecht auf der Ebene und wir spalten sie auf in ihren Anteil senkrecht und parallel zur schiefen Ebene,
und erhalten die allgemeine, geneigte Ebene. In diesem Fall steht die Gewichtskraft nicht mehr senkrecht auf der Ebene und wir spalten sie auf in ihren Anteil senkrecht und parallel zur schiefen Ebene,  und
und  . Die senkrechte Komponente
. Die senkrechte Komponente  wird wieder durch die (jetzt verringerte) Normalkraft
wird wieder durch die (jetzt verringerte) Normalkraft  kompensiert.
kompensiert.
Der parallele Anteil beschleunigt die Masse auf der schiefen Ebene nach unten. Diese Gewichtskraftskomponente wird daher auch Hangabtriebskraft genannt:  . Zudem wirkt auf den Körper eine Reibungskraft, da er auf der Ebene aufliegt (Luftreibung vernachlässigen wir). Ruht der Körper, wirkt der Hangabtriebskraft die Haftreibungskraft
. Zudem wirkt auf den Körper eine Reibungskraft, da er auf der Ebene aufliegt (Luftreibung vernachlässigen wir). Ruht der Körper, wirkt der Hangabtriebskraft die Haftreibungskraft
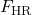 entgegen und wir finden
entgegen und wir finden
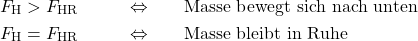 .
.
Die Haftreibungskraft kann in ihrer Wirkung maximal so groß sein wie die Hangabtriebskraft,  (oder allgemein so groß wie die Summe aus allen eine Bewegung einleitenden Kräften). Wäre
(oder allgemein so groß wie die Summe aus allen eine Bewegung einleitenden Kräften). Wäre  größer
größer  , würde sich der Körper aufgrund von Haftreibung nach oben bewegen!
, würde sich der Körper aufgrund von Haftreibung nach oben bewegen!
Bewegt sich der Körper, wirkt die Gleitreibungskraft
 der Bewegung entgegen. Eine Bewegung nach oben wird also in jedem Fall gestoppt und geht entweder in die Ruhelage oder eine Bewegung nach unten über. Bewegt sich der Körper nach unten, kann das entweder beschleunigt
oder mit einer konstanten (Anfangs-)Geschwindigkeit
stattfinden
der Bewegung entgegen. Eine Bewegung nach oben wird also in jedem Fall gestoppt und geht entweder in die Ruhelage oder eine Bewegung nach unten über. Bewegt sich der Körper nach unten, kann das entweder beschleunigt
oder mit einer konstanten (Anfangs-)Geschwindigkeit
stattfinden
 .
.
Wenn wir den Neigungswinkel immer weiter erhöhen, erreichen wir irgendwann den zweiten Spezialfall der schiefen Ebene: die senkrechte Ebene mit einem Neigungswinkel zur Horizontalen von 90 Grad. Hier ist offensichtlich  und die gesamte Gewichtskraft wirkt als Hangabtriebskraft
und die gesamte Gewichtskraft wirkt als Hangabtriebskraft  .
.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Schiefe Ebene Formeln
Sehen wir uns jetzt die Formeln der einzelnen Kräfte auf die Masse an:
Gewichtskraft 

-
 ist die Masse des Körpers,
ist die Masse des Körpers,  ist die Erdbeschleunigung
ist die Erdbeschleunigung - wirkt vertikal nach unten
Hangabtriebskraft 

-
 ist der Neigungswinkel der schiefen Ebene
ist der Neigungswinkel der schiefen Ebene
- wirkt parallel zur Ebene nach unten
Normalkraft 

- wird von der Ebene aufgebracht und kompensiert den Anteil von
 senkrecht zur Ebene (daher betragsmäßig gleich
senkrecht zur Ebene (daher betragsmäßig gleich  )
) - wirkt senkrecht zur Ebene nach oben
Haftreibungskraft 
-
 , mit
, mit 
-
 ist der Haftreibungskoeffizient
ist der Haftreibungskoeffizient -
 wir nicht von
wir nicht von  beschränkt. Ist
beschränkt. Ist  größer als dadurch gegeben, heißt das nur, dass die Haftreibung noch größere Kräfte kompensieren könnte.
größer als dadurch gegeben, heißt das nur, dass die Haftreibung noch größere Kräfte kompensieren könnte. - wirkt stets der einsetzenden Bewegung entgegen (hier also parallel zur Ebene nach oben und entgegen
 , das die Masse nach unten bewegen würde)
, das die Masse nach unten bewegen würde)
Gleitreibungskraft 

-
 ist der Gleitreibungskoeffizient
ist der Gleitreibungskoeffizient - wirkt stets der Bewegung entgegen (hier also zum Beispiel entgegen der Bewegung nach unten auf der Ebene und damit parallel zur Ebene nach oben, entgegen
 )
)
Die Reibungskoeffizienten  und
und  geben an, wie groß die Reibung eines Körpers abhängig von seinem Gewicht, das auf der Ebene lastet, ist. Dabei haben größere Massen offenbar auch eine größere Reibung. Zudem gilt immer
geben an, wie groß die Reibung eines Körpers abhängig von seinem Gewicht, das auf der Ebene lastet, ist. Dabei haben größere Massen offenbar auch eine größere Reibung. Zudem gilt immer  . Also bleibt ein Körper, der aufgrund der Reibung abbremst, dann auch in Ruhe.
. Also bleibt ein Körper, der aufgrund der Reibung abbremst, dann auch in Ruhe.
Schiefe Ebene Aufgaben
Mit dem gewonnenen Wissen zur schiefen Ebene können wir jetzt noch ein paar Beispielaufgaben durchgehen (und dabei noch das eine oder andere Neue lernen).
Aufgabe 1
Sehen wir uns zuerst an, was passiert, wenn wir ein Material, zum Beispiel Erde oder Schnee, auf einen Haufen schaufeln. Wird der Haufen nämlich zu steil, wird das Material nicht mehr halten und an den Seiten wieder abrutschen. Wenn wir die Seiten des Haufens als schiefe Ebenen nähern, wie können wir uns das erklären?
Auf das Material an den Seiten wirken die Hangabtriebskraft  und die Haftreibungskraft
und die Haftreibungskraft  . Damit es herunterfällt, muss gelten
. Damit es herunterfällt, muss gelten
 .
.
Das heißt, wird der Haufen zu hoch und zu steil, also der Neigungswinkel der Seiten zu groß, reicht die Haftreibung nicht mehr aus und das Material fällt zu Boden. Dabei ist zu beachten, dass  . Egal wie hoch die Haftreibung ist, irgendwann fällt jedes Material herunter!
. Egal wie hoch die Haftreibung ist, irgendwann fällt jedes Material herunter!
Aufgabe 2
Mit diesem Wissen betrachten wir jetzt einen Körper auf einer schiefen Ebene mit Winkel  , wobei wir Reibungskoeffizienten von
, wobei wir Reibungskoeffizienten von  und
und  annehmen. Kommt es hier zu einer Bewegung des Körpers und wenn ja, was ist seine Beschleunigung?
annehmen. Kommt es hier zu einer Bewegung des Körpers und wenn ja, was ist seine Beschleunigung?
Die erste Frage beantworten wir durch Berechnung des Tangens
 .
.
Es kommt also zu einer Bewegung nach unten. Jetzt bestimmen wir noch die zugehörige Beschleunigung  :
:
 .
.
Aufgabe 3
Zuletzt sollten wir verstehen, wie schiefe Ebenen verwendet werden können, um leichter schwere Dinge in die Höhe zu transportieren. Dazu sehen wir uns eine schräge Ebene an, die über die (horizontale) Länge  eine Höhe von
eine Höhe von  überwindet und schieben einen
überwindet und schieben einen  schweren Körper (vorerst reibungsfrei) die Rampe hinauf. Wir fragen uns, um wie viel Prozent gegenüber simplem Anheben sich durch die Rampe der Kraftaufwand verringert und ob auch die zu verrichtende Arbeit
dadurch abnimmt. Dann können wir noch die Reibung mit einem Gleitreibungskoeffizienten
schweren Körper (vorerst reibungsfrei) die Rampe hinauf. Wir fragen uns, um wie viel Prozent gegenüber simplem Anheben sich durch die Rampe der Kraftaufwand verringert und ob auch die zu verrichtende Arbeit
dadurch abnimmt. Dann können wir noch die Reibung mit einem Gleitreibungskoeffizienten  ins Spiel bringen und uns fragen, ab wann sich unsere Rampe vom Kraftaufwand her nicht mehr lohnt und wie es jetzt mit der zu verrichtenden Arbeit aussieht.
ins Spiel bringen und uns fragen, ab wann sich unsere Rampe vom Kraftaufwand her nicht mehr lohnt und wie es jetzt mit der zu verrichtenden Arbeit aussieht.
Fangen wir an! Heben wir die Masse einfach an, brauchen wir die volle Gewichtskraft von
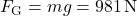 .
.
Auf unserer Rampe benötigen wir aber nur die Hangabtriebskraft von circa
 .
.
Das entspricht einer Verringerung um  ! Bei der Arbeit, die wir verrichten, wenn wir den Körper gegen
! Bei der Arbeit, die wir verrichten, wenn wir den Körper gegen  die Strecke
die Strecke  die Rampe hinauf bewegen, sparen wir jedoch leider nicht, denn es gilt
die Rampe hinauf bewegen, sparen wir jedoch leider nicht, denn es gilt

wie beim Anheben. Diese Betrachtungen waren aber für den reibungslosen Fall. Mit der Reibung benötigen wir zwar mehr Kraft, es soll aber immer noch weniger als  sein. Das heißt,
sein. Das heißt,  darf nicht zu groß sein
darf nicht zu groß sein
 .
.
Unsere Rampe verringert also bis zu einem Gleitreibungskoeffizienten von  unseren Kraftaufwand. Die zu verrichtende Arbeit
unseren Kraftaufwand. Die zu verrichtende Arbeit

ist aber jetzt aufgrund der Reibung immer größer als wenn wir den Körper einfach anheben!


