Video

Quiz

Widerstandsmoment

Das Widerstandsmoment baut auf den Flächenträgheitsmomenten auf und ist ebenfalls eine Größe bezüglich eines Querschnittes im Bauteil.

Möchtest du das Thema Widerstandsmoment kurz und knapp in einem Video erklärt bekommen? Dann schau doch hier mal rein.

Inhaltsübersicht

Widerstandsmoment einfach erklärt

Das Widerstandsmoment lässt sich aus dem Flächenträgheitsmoment bestimmen. Es ist ein Maß dafür, welchen Widerstand ein belasteter Balken oder Bauteil der Entstehung von innerer Spannung entgegensetzt. Unter innerer Spannung versteht man in der Mechanik, die Beanspruchung im Bauteil in Folge einer Belastung von außen.

Es gibt verschiedene Arten von Widerstandsmomente. Da wäre das Biegewiderstandsmoment, welcher auch als axialer Widerstandsmoment bezeichnet wird und das Torsionswiderstandsmoment, den du auch als polaren Wiederstandmoment benennen kannst. Ist ein Balken unter einer Biegebelastung, so führt das zum Biegewiderstandsmoment. Ist die Belastung hingegen eine Torsion, so berechnest du das polare Widerstandsmoment.

Die Formel zur Berechnung des Widerstandsmoment lautet:

$W=\frac{I}{\alpha_{max}}$

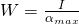
Die Einheit der Berechnung ist [m³]. I ist dabei das Flächenträgheitsmoment und 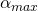$\alpha_{max}$ ist die größte Distanz zwischen Randfaser zu der spannungsfreien Faser, welche aus als neutrale Faser bezeichnet wird. In den Fasern am Rand des Bauteils ist die Beanspruchung des Bauteils am gößten.

Widerstandmoment berechnen

Bei rein elastischen Verformungen werden folgende Formeln verwendet, um die an den Randfasern maximal auftretende Normalspannung zu ermitteln:

$\sigma_{max}=\frac{M_b}{W_{ax}}$

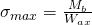
Dabei ist 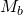M_b der Biegemoment um die Bezugsachse und W_ax das axiale Widerstandsmoment. Wir können die Gleichung auch noch umformen und sehen den Zusammenhang mit dem axialen Flächenträgheitsmoment.

$\sigma_{max}=\frac{a_{max}}{I_{ax}}\ \times M_b$

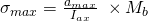
Da wir oben das axiale Widerstandsmoment verwendet haben, ist die Formel für das Biegemoment. Ist ein Trosionsmoment an das Bauteil angebracht, so würde die Formel für die Tangentialspannung so aussehen:

$\tau_{max} = \frac{M_t}{W_p}$

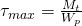
M_t ist dabei das Torsionsmoment und W_p das polare Widerstandsmoment.

Widerstandsmoment Rechteck

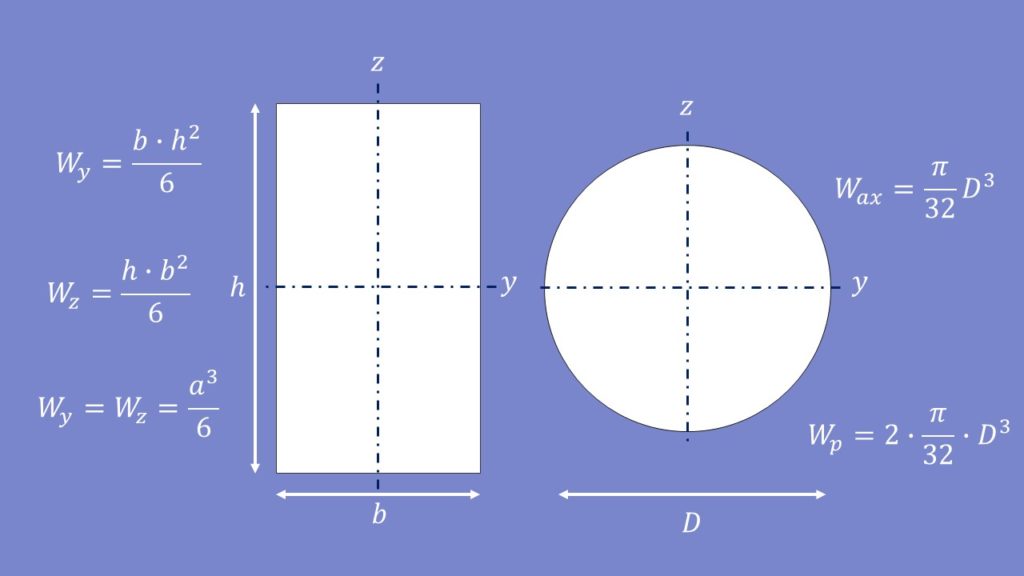
Sehen wir uns nun die polaren Widerstandsmomente für einige Körper an: Beispielsweise für ein Rechteck.

Widerstandsmoment, Widerstandsmoment berechnen, Widerstandsmoment Kreis und Rechteck — Berechnung Rechteck und Kreis

Die Formel für das Widerstandsmoment bezüglich der Horizontalachse hier lautet:

$W_y=\frac{b\times h^2}{6}$

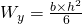
Ähnliches gilt für das Widerstandsmoment bezüglich der Vertikalachse.

$W_z=\frac{h\times b^2}{6}$

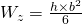
Ist das Rechteck quadratisch kann man folgende Formel anwenden:

$W_y=W_z=\frac{a^3}{6}$

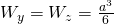
Widerstandsmoment Kreis

Eine weitere mögliche Form wäre ein Kreis mit dem Durchmesser D. Die Formeln für das axiale und das polare Widerstandsmoment lauten hier:

$W_{ax}=\frac{\pi}{32}D^3$

$W_p=2\times\frac{\pi}{32}{\times D}^3$

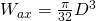
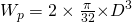
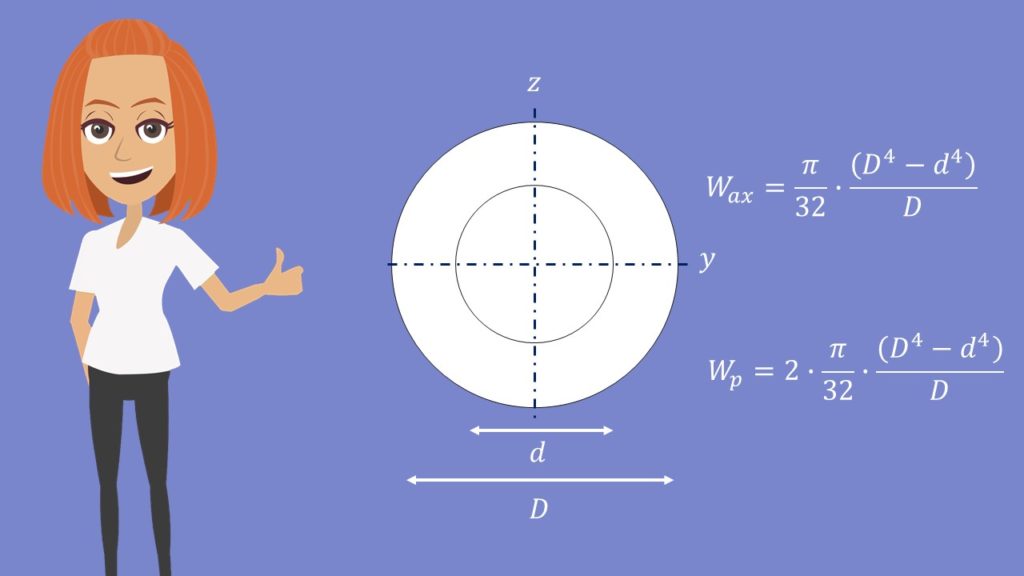
Man kann die Widerstandsmomente auch voneinander abziehen. Haben wir beispielsweise einen Ring bestehend aus zwei Kreisen lautet die Formel:

$W_{ax}=\frac{\pi}{32}\times\frac{\left(D^4-d^4\right)}{D}$

$W_p=2\times\frac{\pi}{32}\times\frac{\left(D^4-d^4\right)}{D}$

Widerstandsmoment, Widerstandsmoment berechnen, Widerstandsmoment Kreis — Ring aus zwei Kreisen

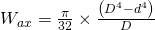
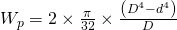
Es gibt natürlich auch noch andere Formen mit speziellen Formeln, die wir jetzt aber nicht alle einzeln behandeln können. Du findest diese in entsprechenden Tabellenwerken in der Literatur oder im Internet. Am Besten du schreibst dir die Formeln, die du benötigst in die Formelsammlung.

zur Videoseite: Widerstandsmoment

Beliebte Inhalte aus dem Bereich Festigkeitslehre

Flächenträgheitsmoment

Flächenträgheitsmomente - Übung

Satz von Steiner

Widerstandsmoment

Mohrscher Spannungskreis

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .