Biegelinie
Du hast doch bestimmt auch schon einmal Skispringen im Fernsehen gesehen? Wie du sicher erkannt hast, biegen sich dabei die Skier durch den Luftwiderstand. Wie sehr sich diese verformen, kannst du mit Hilfe der Biegelinie berechnen.
Inhaltsübersicht
Ermittlung der Biegelinie
Die Biegelinie wird auch als Biegungslinie, als Durchbiegungslinie oder als elastische Linie bezeichnet. Sie beschreibt die Kurve der Verformung eines geraden Balkens bei mechanischer Belastung. Die Berechnung der Biegelinie gehört zur Balkentheorie
. Man verwendet sie, um die Durchbiegung von linear-elastischen Balken zu bestimmen.
Dabei wird die Annahme zugrunde gelegt, dass die eintretenden Verformungen sehr gering sind, so dass die Veränderung der Balkengeometrie in der Aufstellung der Gleichungen vernachlässigt werden kann.
Sehen wir uns nun die Differentialgleichung für den Zusammenhang der Balkenkrümmung und der Biegelinie an:

Die Striche bezeichnen dabei die Ableitung der Biegelinie  in die x-Richtung, also die Länge des Balkens. In den meisten Fällen ist
in die x-Richtung, also die Länge des Balkens. In den meisten Fällen ist  so klein, dass die einfache Ableitung hoch zwei deutlich kleiner als 1 bleibt. Daher wird oft die genäherte Differentialgleichung verwendet.
so klein, dass die einfache Ableitung hoch zwei deutlich kleiner als 1 bleibt. Daher wird oft die genäherte Differentialgleichung verwendet.

Durch zweifaches Aufleiten kann die Biegelinie ermittelt werden.

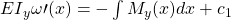

Durch das Aufleiten ergeben sich zwei unbekannte Konstanten  und
und  . Diese können durch Randbedingungen bestimmt werden.
. Diese können durch Randbedingungen bestimmt werden.
Randbedingungen der Biegelinie
Die Rand- und Übergangsbedingungen können sich je nach Lagerungsfall ändern. In der Tabelle kannst du einige der gebräuchlichsten Lagerungsfälle mit ihren Bedingungen sehen.
Nun kannst du die Biegelinie bestimmen.
Wie hängt diese nun mit Moment, Querkraft und Streckenlast zusammen? Ganz einfach!



E mal I wird auch als die Biegesteifigkeit bezeichnet.
Die verschiedenen Größen kannst du auch grafisch darstellen:
Hierbei haben wir einen Balken, der von zwei Festlagern gehalten wird. Die Kraft F drückt von oben auf den Balken. Darunter sehen wir den Biegemoment. Einmal abgeleitet ergibt sich der Querkraftverlauf. W entspricht der Biegelinie.
Sehr schön! Nun weißt du worauf du bei der Biegelinie achten musst und wie du Sie bestimmen kannst.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel zur Einzellast
Das wollen wir doch gleich mal an einem Beispiel probieren. Fangen wir an mit einem Körper, der mit einer Einzellast belastet wird. Dazu betrachten wir ein Kragram. Ein Kragarm ist ein Balken, der am linken Rand fest eingespannt ist und am rechten Rand ein freies Ende besitzt. Der betrachtete Balken hat die Länge L gleich ein Meter, den E-Modul E gleich 210.000MPa und das Flächenträgheitsmoment  gleich 290.000 Millimeter hoch vier. Das Koordinatensystem legen wir in die Einspannung, wobei x nach rechts und z nach unten zeigt.
gleich 290.000 Millimeter hoch vier. Das Koordinatensystem legen wir in die Einspannung, wobei x nach rechts und z nach unten zeigt.
Den Balken wollen wir jetzt unter dem folgenden Lastfall betrachten:
Eine Einzelkraft F gleich 800 Newton greift am Balkenende an.
Für diesen Fall wollen wir nun die Gleichung der Biegelinie bestimmen.
Momentenverlauf
Zu Beginn müssen wir den Momentenverlauf über den Balken mit Hilfe der Schnittgrößen bestimmen. Dieser ergibt sich für uns zu:

Wenn dir das zu schnell ging, schau dir am besten noch mal das Video zu Schnittgrößen an.
Integrationskonstanten berechnen
Um die Integrationskonstanten zu bestimmen, verwenden wir folgende Randbedingungen am Balken:
- Die Einspannung: Biegelinie
 und Krümmung der Biegelinie
und Krümmung der Biegelinie  sind hier Null. Querkraft und Moment sind unbekannt.
sind hier Null. Querkraft und Moment sind unbekannt. - Das Festlager: Biegelinie
 und Moment sind hier Null, Querkraft und Krümmung
und Moment sind hier Null, Querkraft und Krümmung  sind unbekannt und
sind unbekannt und - Der freie Rand: Biegelinie
 und Krümmung
und Krümmung  sind hier unbekannt. Querkraft und Moment sind Null.
sind hier unbekannt. Querkraft und Moment sind Null.
Wir setzen die Formel des Momentenverlaufs in die Gleichung für die zweite Ableitung der Biegelinie ein und erhalten damit:

Daraus ergibt sich durch Integration die Krümmung:


Und anschließend durch eine weitere Integration die Biegelinie:

Die Integrationskonstanten erhalten wir jetzt mit Hilfe der Randbedingungen. Da wir links eine Einspannung haben, wissen wir, dass dort die Krümmung und die Biegelinie gleich Null sein müssen. Damit ergeben sich aus den Randbedingungen zwei Gleichungen:


Du siehst sicher schnell, dass in diesem Fall sowohl  , als auch
, als auch  gleich Null sein müssen. So ergibt sich für die gesamte Biegelinie:
gleich Null sein müssen. So ergibt sich für die gesamte Biegelinie:

Damit haben wir die Funktion der Biegelinie bestimmt und die Aufgabe gelöst! Wenn du dir das nochmal ausführlicher anschauen willst, solltest du unser Video Biegelinie berechnen – Einzellast nicht verpassen.
Beispiel zur Dreieckslast
Um das Ganze noch an der Dreieckslast
zu üben, haben wir hier ein Beispiel für dich. Wir haben den gleichen Kragarm wie bei der Einzellast vorliegen. Der betrachtete Balken hat die Länge L gleich ein Meter, den E-Modul E gleich 210.000MPa und das Flächenträgheitsmoment  gleich 290.000 Millimeter hoch vier. Das Koordinatensystem legen wir in die Einspannung, wobei x nach rechts und z nach unten zeigt.
gleich 290.000 Millimeter hoch vier. Das Koordinatensystem legen wir in die Einspannung, wobei x nach rechts und z nach unten zeigt.
Streckenlast berechnen
Den Balken wollen wir jetzt unter einem zweiten Lastfall betrachten:
Eine Dreieckslast  mit q Null gleich 5 Kilonewton pro Meter.
mit q Null gleich 5 Kilonewton pro Meter.
Da wir nun einen Lastverlauf betrachten, können wir die bekannte Formel für die Biegelinie nicht mehr so einfach verwenden. Das liegt daran, dass wir den Momentenverlauf benötigen, wir ihn aber nicht so schnell bestimmen können. Um das Problem zu lösen, denken wir nochmal zurück an die Schnittgrößen: wenn wir den Momentenverlauf zweimal ableiten, erhalten wir die Streckenlast. Das heißt, wir müssen die Biegelinie noch zweimal ableiten und es ergibt sich:

Setzen wir die Funktion für die Dreieckslast ein, erhalten wir für die vierte Ableitung:

Das integrieren wir nun viermal. Die erste Integration ergibt:

Nach der zweiten Integration erhalten wir:

Und nach der dritten:

Und schließlich ergibt sich w2 von x mit:


Du siehst: wir erhalten außerdem die vier Integrationskonstanten C eins, C zwei, C drei und C vier.
Randbedingungen
Welche Randbedingungen, können wir jetzt anwenden? Betrachten wir die dritte Ableitung der Biegelinie, erkennst du vielleicht aus den Schnittgrößen, dass es sich um den Querkraftverlauf handelt, wenn wir nicht durch E mal J22 teilen würden. Wir hätten dann also die erste Ableitung des Momentenverlaufs, der schließlich den Querkraftverlauf darstellt.

Das heißt die dritte Ableitung ist auch Null, wenn der Querkraftverlauf Null ist. In unserem Fall muss die Querkraft am Balkenende, also x gleich L, Null sein. Für die zweite Ableitung wissen wir ja, dass der Momentenverlauf ausschlaggebend ist. Ist jetzt das Moment an einer Stelle gleich Null, ist dann folglich auch die zweite Ableitung der Biegelinie gleich Null. Das finden wir am Balkenende, also bei x gleich L.
Damit erhalten wir für die dritte Ableitung der Biegelinie am Balkenende:

Es ergibt sich nun:

Für die zweite Ableitung erhalten wir dann:

Stellen wir diese Gleichung jetzt nach C zwei um, erhalten wir:

Damit haben wir die ersten beiden Integrationskonstanten bestimmt. Die anderen beiden ermitteln wir jetzt genauso wie vorher mit der Bedingung, dass an der Einspannung sowohl Biegelinie, als auch Krümmung Null sein müssen. An der Einspannung erhalten wir dann für die Krümmung:

Um die Gleichung zu erfüllen, muss C drei Null sein. An der Einspannung ergibt sich für die Biegelinie:

Damit muss auch C vier gleich Null sein und wir erhalten unsere gesamte Formel für die Biegelinie ohne Werte:

Setzten wir die Werte für L, q Null, E und J zwei zwei ein und ziehen x Quadrat vor die Klammern, erhalten wir:
So, jetzt weißt du auch wie du vorgehen musst, wenn du es mit einer Streckenlast zu tun bekommst.



