Elastizitätsmodul
In diesem Beitrag wollen wir dir den Elastizitätsmodul näherbringen. Wir werden dir unter anderem erklären, was der Elastizitätsmodul ist und welche Formeln es dazu gibt.
Du würdest dir die Erklärung lieber anhören als lesen? Keine Sorge! Wir haben zum Elastizitätsmodul ein Video , worin du in kürzester Zeit das Nötigste beigebracht bekommst.
Inhaltsübersicht
Elastizitätsmodul einfach erklärt
Der Elastizitätsmodul (auch Zugmodul, Elastizitätskoeffizient, Dehnungsmodul, oder Youngscher Modul; wird oft mit E-Modul abgekürzt) beschreibt das Verhältnis zwischen Spannung und der daraus resultierenden Dehnung eines Körpers

Im Spannungs-Dehnungs-Diagramm entspricht die Steigung im Bereich der elastischen Verformung gerade dem Elastizitätsmodul
 .
.
Der Elastizitätsmodul ist eine Materialkonstante mit der Einheit  , häufiger aber in
, häufiger aber in  angegeben.
angegeben.
Mit den Formeln
 für die Spannung
für die Spannung
und
 für die Dehnung
für die Dehnung
erhalten wir den Zusammenhang
 .
.
Hier ist  die Kraft, die auf einem Stab wirkt,
die Kraft, die auf einem Stab wirkt,  die Querschnittsfläche des Stabes,
die Querschnittsfläche des Stabes,  die Ruhelänge des Stabes und
die Ruhelänge des Stabes und  die durch die Kraft hervorgerufene Längenänderung des Stabes. In dieser Form lässt sich die Formel mit der Merkregel „FLEA“ leicht einprägen.
die durch die Kraft hervorgerufene Längenänderung des Stabes. In dieser Form lässt sich die Formel mit der Merkregel „FLEA“ leicht einprägen.
Spannungs-Dehnungs-Diagramm
Das Spannungs-Dehnungs-Diagramm eines Materials wird mit Hilfe eines Zugversuches
aufgenommen. Dabei wird ein Körper bekannter Ruhelänge  und Querschnittsfläche
und Querschnittsfläche  durch eine kontinuierlich steigende Kraft gedehnt. Für jeden Kraftwert wird die Längenänderung
durch eine kontinuierlich steigende Kraft gedehnt. Für jeden Kraftwert wird die Längenänderung  bestimmt. Mit den Daten bildet man dann die Verhältnisse
bestimmt. Mit den Daten bildet man dann die Verhältnisse  für die Spannung
für die Spannung  und
und  für die Dehnung
für die Dehnung  . Im Diagramm wird dann die Spannung vertikal, die dadurch hervorgerufene Dehnung horizontal aufgetragen. Ein typisches Diagramm sieht dabei folgendermaßen aus.
. Im Diagramm wird dann die Spannung vertikal, die dadurch hervorgerufene Dehnung horizontal aufgetragen. Ein typisches Diagramm sieht dabei folgendermaßen aus.
Im Diagramm wird der Bereich, in dem das Verhältnis zwischen Spannung und Dehnung linear ist, als elastischer Bereich bezeichnet. Der Punkt, ab dem das lineare Verhältnis verloren geht, heißt Elastizitätsgrenze (auch Streckgrenze). Innerhalb des elastischen Bereichs wird von einer elastischen Verformung gesprochen. Der Prüfkörper kehrt hier zu seiner ursprünglichen Form zurück, sobald keine Kraft mehr auf ihn ausgeübt wird.
Wird der Körper über die Elastizitätsgrenze hinaus gedehnt, gelangt man in den plastischen Bereich. Hier bleiben die Verformungen, auch wenn auf dem Körper keine Kraft mehr wirkt. Die Dehnung im elastischen Bereich geschieht durch die Veränderung der Atomabstände innerhalb des Körpers. Plastische Verformung hingegen findet durch die Erzeugung und Bewegung von Versetzungen innerhalb des Körpers statt. Am rechten Ende des Diagramms findet man den Bruchpunkt. Hier wird die maximale Dehnung erreicht, ab der dann der Körper reißt. Die dazugehörige Spannung wird als Festigkeit des Prüfkörpers bezeichnet.
Hat man zu einem beliebigen Körper das Spannungs-Dehnungs-Diagramm, dann kann man innerhalb des elastischen Bereiches die Steigung  ausrechnen. Diese Steigung entspricht dann genau dem Elastizitätsmodul des Prüfkörpers
ausrechnen. Diese Steigung entspricht dann genau dem Elastizitätsmodul des Prüfkörpers
 .
.
Hookesches Gesetz
Für das Experiment betrachten wir einen quaderförmigen Körper der Länge  und Querschnittsfläche
und Querschnittsfläche  . Wir interessieren uns wie sich die Kraft verhält, die notwendig ist, um eine Längenänderung
. Wir interessieren uns wie sich die Kraft verhält, die notwendig ist, um eine Längenänderung  zu erzielen. Sofern wir uns im elastischen Bereich des Körpers befinden, zeigen Experimente (z.B. das des Spannungs-Dehnungs-Diagrammes), dass folgendes gilt
zu erzielen. Sofern wir uns im elastischen Bereich des Körpers befinden, zeigen Experimente (z.B. das des Spannungs-Dehnungs-Diagrammes), dass folgendes gilt
 .
.
Das heißt, die für eine Längenänderung  notwendige Kraft
notwendige Kraft  ist direkt proportional zur Längenänderung selbst. Diese Gesetzmäßigkeit wird auch als Hookesches Gesetz
bezeichnet. Würde man an dieser Stelle die Proportionalitätskonstante
ist direkt proportional zur Längenänderung selbst. Diese Gesetzmäßigkeit wird auch als Hookesches Gesetz
bezeichnet. Würde man an dieser Stelle die Proportionalitätskonstante  einführen, dann könnte man die Beobachtung formulieren als
einführen, dann könnte man die Beobachtung formulieren als
 ,
,
die sogenannte Federkraft. Wenn du mehr zur Federkraft
oder der Federkonstanten
 erfahren möchtest (zum Beispiel woher das Minuszeichen kommt), dann erreichst du durch das Anklicken der Verlinkungen unsere Beiträge zu diesem Themen.
erfahren möchtest (zum Beispiel woher das Minuszeichen kommt), dann erreichst du durch das Anklicken der Verlinkungen unsere Beiträge zu diesem Themen.
Einfluss der geometrischen Abmessungen
Wir interessieren uns aber welchen Einfluss die geometrischen Abmessungen des Körpers haben. Wenn du jetzt zwei identische Körper nimmst und auf jeden die Kraft  ausübst, dann ändert sich die Länge jeweils um
ausübst, dann ändert sich die Länge jeweils um  . Klebst du die beiden Körper zusammen, dann ändert sich daher die Länge des neuen Körpers mit der Länge
. Klebst du die beiden Körper zusammen, dann ändert sich daher die Länge des neuen Körpers mit der Länge  um den Betrag
um den Betrag  . Diese Beobachtung bedeutet, dass die Längenänderung
. Diese Beobachtung bedeutet, dass die Längenänderung  abhängig von der Ruhelänge
abhängig von der Ruhelänge  des Körpers ist. Um diese Abhängigkeit zu eliminieren, wird das Verhältnis betrachtet und man erhält
des Körpers ist. Um diese Abhängigkeit zu eliminieren, wird das Verhältnis betrachtet und man erhält
 ,
,
die nun unabhängig von der Ruhelänge  ist.
ist.
Wenn du jetzt die zwei identischen Körper Seite an Seite zusammenklebst, dann brauchst du für eine gegebene Längenänderung  für beide Seiten eine Kraft
für beide Seiten eine Kraft  . Insgesamt brauchst du für den neuen Körper mit der Querschnittsfläche
. Insgesamt brauchst du für den neuen Körper mit der Querschnittsfläche  eine Kraft von
eine Kraft von  , um die Längenänderung
, um die Längenänderung  zu erzielen. Wir erhalten somit
zu erzielen. Wir erhalten somit
 .
.
Führen wir den Proportionalitätsfaktor E ein, bekommen wir insgesamt also
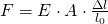
für die Kraft, die notwendig ist, um den Körper um den Betrag  zu dehnen. Wenn wir diese Kraft mit der Federkraft vergleichen (und die Änderung
zu dehnen. Wenn wir diese Kraft mit der Federkraft vergleichen (und die Änderung  mit der Änderung
mit der Änderung  gleichsetzen) erhalten wir das Hookesches Gesetz wieder mit der Federkonstanten
gleichsetzen) erhalten wir das Hookesches Gesetz wieder mit der Federkonstanten  . Der eingeführte Faktor heißt Elastizitätsmodul. Anders als die Federkonstante hängt der Elastizitätsmodul nicht von den geometrischen Abmessungen des Körpers ab. Stellst du die Formel nach
. Der eingeführte Faktor heißt Elastizitätsmodul. Anders als die Federkonstante hängt der Elastizitätsmodul nicht von den geometrischen Abmessungen des Körpers ab. Stellst du die Formel nach  um, erhältst du die gewünschte FLEA-Formel.
um, erhältst du die gewünschte FLEA-Formel.
Elastizitätsmodul ausgewählter Materialien
In diesem Abschnitt zeigen wir dir die Elastizitätsmodule einiger Materialien und besprechen im Anschluss dazu die Unterschiede zu den weiteren Kenngrößen Steifigkeit, Härte und Zähigkeit.
| Material | Elastizitätsmodul  ( ( ) ) |
| Stahl |  |
| Gusseisen |  |
| Aluminium |  |
| Messing |  |
| Beton |  |
| Granit |
 |
| Holz (parallel zur Maserung) |  |
| Holz (senkrecht zur Maserung) |  |
| Knochen |  |
Wie du der Tabelle entnehmen kannst, ist der Elastizitätsmodul von Festkörpern ziemlich groß. In der Praxis nimmt man daher häufig auch die Einheit GPa für Gigapascal her. Der Elastizitätsmodul von Stahl ist dann  , der Elastizitätsmodul von Aluminium
, der Elastizitätsmodul von Aluminium  . Für Holz muss man den Elastizitätsmodul in zwei Richtungen messen. Das liegt daran, dass Holz ein anisotropes Material ist. In solchen Materialien ist der Elastizitätsmodul richtungsabhängig und muss durch den Spannungstensor
beschrieben werden.
. Für Holz muss man den Elastizitätsmodul in zwei Richtungen messen. Das liegt daran, dass Holz ein anisotropes Material ist. In solchen Materialien ist der Elastizitätsmodul richtungsabhängig und muss durch den Spannungstensor
beschrieben werden.
Steifigkeit, Härte und Zähigkeit
Die Steifigkeit eines Körpers beschreibt den Widerstand des Körpers gegenüber elastischer Verformung durch Kräfte. Anders als der Elastizitätsmodul hängt die Steifigkeit eines Körpers von den geometrischen Abmessungen des Körpers ab.
Die Härte eines Körpers beschreibt den Widerstand des Körpers gegen das mechanische Eindringen eines anderen Körpers. Die Härte eines Körpers tendiert mit steigendem Elastizitätsmodul ebenfalls zu steigen. Der Elastizitätsmodul ist aber nicht alleine für die Härte eines Körpers verantwortlich. Die Streckgrenze spielt dabei auch eine Rolle.
Die Zähigkeit beschreibt die Menge an Energie, die ein Körper aufnehmen kann, bevor es unter Belastung bricht. Während der Elastizitätsmodul der Steigung im elastischen Bereich des Spannungs-Dehnungs-Diagrammes entspricht, ist die Zähigkeit gerade die Fläche unter dem Graphen.
Elastizitätsmodul berechnen
Wollen wir uns zum Abschluss ein kleines Zahlenbeispiel anschauen. Wir betrachten dazu eine Gitarrensaite aus Stahl der Länge  mit einem Durchmesser von
mit einem Durchmesser von  . Welche Kraft ist notwendig, um die Gitarrensaite um den Betrag
. Welche Kraft ist notwendig, um die Gitarrensaite um den Betrag  zu dehnen?
zu dehnen?
Wir nehmen dazu die FLEA-Formel und stellen sie nach der Kraft  um. Die Querschnittsfläche
um. Die Querschnittsfläche  der Saite entspricht
der Saite entspricht  . Damit berechnet sich die gesuchte Kraft zu
. Damit berechnet sich die gesuchte Kraft zu
 .
.
Der Elastizitätsmodul von Stahl wurde dabei der Tabelle oben entnommen.
