Fermi Energie
Mit der Fermi Energie kannst du die höchste Energie eines Teilchens in einem System von Fermionen bei einer Temperatur von null Kelvin ( ) berechnen. In diesem Artikel erklären wir dir, was die Fermi Energie genau beschreibt und wie du sie berechnen und herleiten kannst. Darüber hinaus erfährst du, wie du mit ihr Materialien, insbesondere Metalle, Halbleiter und Isolatoren, charakterisieren kannst und was bei Temperaturen höher als 0 Kelvin passiert. Am Ende des Artikels werden wir uns auch ein konkretes Beispiel ansehen, indem wir die Fermi Energie explizit für Kupfer berechnen.
) berechnen. In diesem Artikel erklären wir dir, was die Fermi Energie genau beschreibt und wie du sie berechnen und herleiten kannst. Darüber hinaus erfährst du, wie du mit ihr Materialien, insbesondere Metalle, Halbleiter und Isolatoren, charakterisieren kannst und was bei Temperaturen höher als 0 Kelvin passiert. Am Ende des Artikels werden wir uns auch ein konkretes Beispiel ansehen, indem wir die Fermi Energie explizit für Kupfer berechnen.
Du möchtest ein wenig relaxen, dich zurücklehnen und trotzdem alles Wichtige zur Fermi Energie erfahren, was du wissen musst? Dann schau ganz entspannt unser Video dazu an!
Inhaltsübersicht
Fermi Energie einfach erklärt
Die Fermi Energie gibt die Energie des höchsten besetzten Energieniveaus im Grundzustand eines Systems aus Fermionen an.
Betrachtest du den absoluten Nullpunkt (0 Kelvin), dann sind alle Energieniveaus bis zur Fermi Energie voll besetzt und die höheren Energieniveaus sind unbesetzt. Dabei ist ein System im Grundzustand, wenn es sich im Zustand geringstmöglicher Energie befindet.
Fermi Energie Formel
Die Fermi Energie lässt sich für ein Gas aus nicht-wechselwirkenden Fermionen berechnen mit der Formel

Dabei repräsentiert  das reduzierte Plancksche Wirkungsquantum,
das reduzierte Plancksche Wirkungsquantum,  die Masse des Fermions und
die Masse des Fermions und  den Fermi-Wellenvektor
den Fermi-Wellenvektor

Die Teilchendichte  ist hierbei der Quotient aus der Teilchenzahl
ist hierbei der Quotient aus der Teilchenzahl  und dem Volumen
und dem Volumen  . Unter Verwendung der Fermi Energie kann man auch die Fermi-Geschwindigkeit einfach berechnen mit
. Unter Verwendung der Fermi Energie kann man auch die Fermi-Geschwindigkeit einfach berechnen mit

Die Fermi-Geschwindigkeit 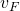 ist dabei die Geschwindigkeit eines Fermions, bei welchem die kinetische Energie
ist dabei die Geschwindigkeit eines Fermions, bei welchem die kinetische Energie  gleich der Fermi Energie
gleich der Fermi Energie  entspricht
entspricht

Mit dem Fermi-Wellenvektor lässt sich auch die sogenannte Fermi-Wellenlänge  ausdrücken
ausdrücken

Fermionen, wie zum Beispiel Elektronen, breiten sich sowohl als Welle wie auch als Teilchen aus. Die Fermi-Wellenlänge ist dabei die Wellenlänge der Elektronen, welche sie bei der Fermi-Energie besitzen. Außerdem lässt sich aus der Fermi-Energie auch die sogenannte Fermi-Temperatur  berechnen
berechnen

wobei  die Boltzmann-Konstante bezeichnet.
die Boltzmann-Konstante bezeichnet.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Fermi Energie Herleitung
In diesem Abschnitt werden wir die Formel für die Fermi Energie herleiten. Dabei gehen wir von einem quadratischen Potentialkasten mit dem Volumen  aus. Zusätzlich werden die Fermionen als nicht-wechelwirkende Teilchen genähert und das System befinde sich im Grundzustand bei einer Temperatur von 0 Kelvin. Da man von einem unendlichen, periodischen Potential ausgeht, gilt für die Wellenfunktion
aus. Zusätzlich werden die Fermionen als nicht-wechelwirkende Teilchen genähert und das System befinde sich im Grundzustand bei einer Temperatur von 0 Kelvin. Da man von einem unendlichen, periodischen Potential ausgeht, gilt für die Wellenfunktion 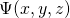

Durch lösen der stationäre Schrödingergleichung mit der Bloch-Funktion erhält man dann als Bedingung für den Wellenzahlvektor
(1)  mit
mit  .
.
Aus der Teilchenphysik ist außerdem die folgende Beziehung zwischen der Frequenz und der Energie bekannt

Zusätzlich weiß man auch, dass die Wellenzahl  proportional zum Impuls
proportional zum Impuls  ist
ist

Verwendet man diese Beziehungen, so erhält man für die kinetische Energie folgende Formel

Setzt man in diese Formel für den Wellenvektor  den Fermi-Wellenvektor
den Fermi-Wellenvektor  ein, dann resultiert daraus die Fermi Energie
ein, dann resultiert daraus die Fermi Energie
(2) 
Alle Energieniveaus sind im Grundzustand dann bis zu dieser Fermi-Energie mit jeweils zwei Spins besetzt. Diese besetzten Zustände befinden sich dabei in der Fermi-Kugel mit dem Volumen

Das Volumen  , welches genau einen Zustand enthält, hat dabei im reziproken Raum ein Volumen von
, welches genau einen Zustand enthält, hat dabei im reziproken Raum ein Volumen von

Teilt man nun das Volumen der Fermi-Kugel durch das Volumen  , dann erhält man daraus die Anzahl
, dann erhält man daraus die Anzahl  der Elektronen im Potentialkasten
der Elektronen im Potentialkasten

Der Faktor 2 kommt daher, da jeder Zustand zwei Elektronen aufnehmen kann. Hiermit lässt sich nun einfach die Elektronendichte  bestimmen
bestimmen

Formt man diese Gleichung nach  um
um

und setzt dies in die Formel (2) ein, dann kann man die Fermi Energie auch mit der Teilchendichte  ausdrücken
ausdrücken

Fermi Energie Halbleiter, Isolator, Metall
Mit der Fermi Energie kann man nun erklären, weshalb manche Materialien leitend sind und manche nicht. Befindet sich die Fermi Energie in der Bandlücke zwischen dem vollbesetzten Valenzband und dem leeren Leitungsband so können durch, zum Beispiel (genügend starke) thermische Anregung, Elektronen in das Leitungsband gelangen. Damit wird das Material leitend und man spricht in diesem Fall von einem Halbleiter. Ist die Bandlücke jedoch zu groß, sodass die Elektronen diese durch Anregung nicht überbrücken können, dann ist das Material nicht leitend und man spricht von einem Isolator. Bei einem Metall handelt es sich um ein leitendes Material, da sich die Fermi Energie im Leitungsband befindet und somit das Leitungsband teilweise besetzt ist. Und teilweise besetzte Bänder sind gerade die Voraussetzung, dass ein Material leitend ist.
Fermi Kante bei höheren Temperaturen
Die Zustände sind bei einer Temperatur von 0 Kelvin gerade bis zum Fermi Niveau besetzt. Man spricht in diesem Zusammenhang auch von einer Fermi-Kante, da die Fermi-Verteilung  für
für  eine Kante aufweist. Die Fermi-Verteilung gibt dabei die Wahrscheinlichkeit an mit welcher ein Zustand mit der Energie
eine Kante aufweist. Die Fermi-Verteilung gibt dabei die Wahrscheinlichkeit an mit welcher ein Zustand mit der Energie  bei einer bestimmten Temperatur
bei einer bestimmten Temperatur  besetzt ist
besetzt ist

Hierbei ist  das chemische Potential und für
das chemische Potential und für  gilt
gilt  . Bis zur Energie der Fermi-Kante sind also alle Zustände besetzt und die Zustände höherer Energie sind alle unbesetzt. Wird die Temperatur ausgehend von 0 Kelvin erhöht, so weicht die Fermi-Kante immer mehr auf und es werden auch Zustände über dem Fermi Niveau besetzt. Dies ist in der folgenden Abbildung gut zu erkennen.
. Bis zur Energie der Fermi-Kante sind also alle Zustände besetzt und die Zustände höherer Energie sind alle unbesetzt. Wird die Temperatur ausgehend von 0 Kelvin erhöht, so weicht die Fermi-Kante immer mehr auf und es werden auch Zustände über dem Fermi Niveau besetzt. Dies ist in der folgenden Abbildung gut zu erkennen.
Dabei muss jedoch gelten, dass die thermische Energie 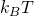 viel kleiner ist als die Fermi Energie
viel kleiner ist als die Fermi Energie

Fermi Energie berechnen Beispiel
Mit der oben genannten Formel lässt sich nun einfach die Fermi Energie verschiedener Elemente berechnen, wie zum Beispiel die Fermi Energie Natrium oder die Fermi Energie Kupfer. Hier wollen wir als Beispiel die Fermi Energie Kupfer berechnen. Die freien Elektronen in Kupfer haben bei  eine Dichte von
eine Dichte von  , die Masse von Elektronen ist gegeben durch
, die Masse von Elektronen ist gegeben durch  und das reduzierte Plancksche Wirkungsquantum mit
und das reduzierte Plancksche Wirkungsquantum mit  . Damit erhält man die Fermi Energie Kupfer
. Damit erhält man die Fermi Energie Kupfer



