Was bedeutet die Wellenfunktion physikalisch?

Die Wellenfunktion beschreibt den quantenmechanischen Zustand eines Teilchens als orts- und zeitabhängige Größe. Aus ihr lässt sich ableiten, wie sich der Zustand mit der Zeit entwickelt, wenn der Energieoperator (Hamilton-Operator) wirkt. Physikalisch gibt die Wahrscheinlichkeitsdichte für einen Messort an.

Woran erkennt man, ob man die zeitabhängige oder die stationäre Schrödinger-Gleichung benutzen muss?

Die zeitabhängige Schrödinger-Gleichung benutzt man, wenn sich der betrachtete Zustand oder das Potential mit der Zeit ändern kann, also wenn Größen ausdrücklich von abhängen. Die stationäre Schrödinger-Gleichung passt, wenn und das Potential nur vom Ort abhängen und man feste Energiewerte eines Zustands sucht.

Warum gibt es im Potentialtopf nur bestimmte erlaubte Energien und nicht jeden beliebigen Wert?

Im Potentialtopf entstehen nur bestimmte erlaubte Energien, weil die Wellenfunktion an den festen Randpunkten passende Randbedingungen erfüllen muss. Dadurch passen nur bestimmte stehende Wellen in die Länge , also nur bestimmte Wellenlängen. Weil die Energie von dieser Wellenlänge abhängt, werden die Energien diskret.

Was sagt die Hauptquantenzahl beim Wasserstoffatom über den Zustand des Elektrons aus?

Die Hauptquantenzahl kennzeichnet beim Wasserstoffatom das Energieniveau eines Elektronenzustands. Sie kann nur positive natürliche Zahlen annehmen und bestimmt über , wie stark der Zustand gebunden ist. Größeres bedeutet weniger negative Energie und größere typische Ausdehnung.

Video

Hier geht's zum Video „Partielle DGL“

Hier geht's zum Video „Interferenz“

Hier geht's zum Video „Elementarteilchen“

Hier geht's zum Video „Plancksches Wirkungsquantum“

Hier geht's zum Video „Elektron“

Hier geht's zum Video „Elektrisches Potential“

Zurück zum Text

Weiter lernen Empfohlenes passendes Video

Schrödinger Gleichung

Wichtige Inhalte in diesem Video

Schrödinger Gleichung einfach erklärt

(00:11)

Schrödinger Gleichung Herleitung

(01:16)

Schrödinger Gleichung Schule

(01:48)

Stationäre Schrödinger Gleichung

(02:27)

Schrödinger Gleichung Wasserstoff

(02:43)

Was die Schrödinger Gleichung ist und was sie überhaupt aussagt, genau das erfährst du hier.

Schau dir auf jeden Fall noch das Video zum Artikel an. Darin sind alle wichtigen Informationen für dich audiovisuell aufbereitet.

Inhaltsübersicht

Schrödinger Gleichung einfach erklärt

im Videozur Stelle im Video springen

(00:11)

Die Schrödinger Gleichung ist das Fundament für fast alle praktischen Anwendungen der Quantenmechanik. Sie beschreibt in Form einer partiellen Differenzialgleichung, die Veränderung eines physikalischen, nicht relativistischen Zustandes nach den Regeln der Quantenmechanik.

Dieser physikalische Zustand ist durch eine Wellenfunktion in der Schrödinger Gleichung repräsentiert. Die Wellenfunktion verändert sich mit der Zeit, aufgrund der Anwendung des Hamilton Operators auf diese. Beim Hamilton Operator handelt es sich um den Energie Operator der Quantenmechanik. Mit ihm gibst du Energiemesswerte und die Zeitentwicklung an.

Daher verändert die Wellenfunktion ihre Form in Abhängigkeit von der Zeit. Du beschreibst damit Prozesse wie die Ausbreitung, Streuung und Interferenz von Teilchen . Mit der Schrödinger Gleichung berechnest du die Energieniveaus der physikalischen Zustände.

Schrödinger Gleichung Herleitung

im Videozur Stelle im Video springen

(01:16)

Du kannst die Schrödinger Gleichung nicht aus der klassischen Physik herleiten. Sie ist ein Postulat, das jedoch aus der Hamiltonfunktion eines gegebenen Problems herleitbar ist.

Eine solche Hamiltonfunktion hat die Form:

$E= \frac{p^2}{2m} + V(r,t)$

Hierbei steht für die Energie, für das Potential, für den Impuls, für die Masse, für den Ort und für die Zeit. Daraus leitest du die Schrödinger Gleichung her, indem du diese klassischen Größen durch entsprechende, quantenmechanische Operatoren ersetzt.

$E \rightarrow \^{E} = i \hbar \frac{\partial}{\partial t}$

$p \rightarrow \^{p} = -i \hbar \nabla$

$r \rightarrow \^{r} = r$

ist die imaginäre Einheit $\sqrt{-1}=i$ , $\frac{\partial}{\partial t}$ eine partielle Ableitung (in diesem Fall nach der Zeit) und $\hbar$ das reduzierte plancksche Wirkungsquantum $\hbar = \frac{h}{2 \pi}$ . Zudem brauchst du für den Impulsoperator $\^{p}$ den sogenannten Nabla-Operator $\nabla$ . Bei diesem Operator handelt es sich um einen Vektor , in welchem jedes Element die partielle Ableitung nach einer Raumdimension darstellt $\vec{\nabla} = \left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}\right)$ .

Wendest du diese Operatoren nun auf deine Wellenfunktion $\psi = \psi (r,t)$ an erhältst du die Schrödinger Gleichung.

$i \hbar \frac{\partial \psi}{\partial t} = - \frac{\hbar ^2}{2m} \Delta \psi + V \psi$

Hier siehst du einen neuen Operator $\Delta$ . Dieser heißt Laplace-Operator und ergibt sich aus dem Skalarprodukt $\nabla ^2 = \Delta = \left(\frac{\partial ^2}{\partial x^2}, \frac{\partial ^2}{\partial y^2}, \frac{\partial ^2}{\partial z^2}\right)$ . Damit handelt es sich bei ihm um einen Vektor, in welchem jedes Element eine partielle, zweite Ableitung nach einer Raumdimension darstellt.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Nach Beantwortung speichern wir deine Antwort, um Studyflix zu verbessern. Mehr dazu erfährst du in unserer Datenschutzerklärung.

Schrödinger Gleichung Schule

im Videozur Stelle im Video springen

(01:48)

In der Schule lernst du wahrscheinlich eine einfachere Form der Schrödinger Gleichung kennen. Diese ist die stationäre, eindimensionale Schrödinger Gleichung. Mit ihr ist es dir möglich einfachere Probleme zu lösen ohne Kenntnisse über Operatoren, komplexe Zahlen, partielle Ableitung und ähnliches zu haben.

Du fängst an, indem du dir die Schrödinger Gleichung aufschreibst:

$E \psi (x) = \^{H} \psi (x)$

Du schreibst den Hamilton-Operator $\^{H}$ aus und erhältst

$E \psi (x) = \left( - \frac{\hbar ^2}{2m} \nabla ^2 + V(x) \right) \psi (x)$

Jetzt schreibst du den Nabla-Operator aus und löst die Klammern auf

$E \psi = - \frac{\hbar ^2}{2m} \frac{\partial ^2}{\partial x^2} \psi (x) + V(x) \psi (x)$

Durch Äquivalenzumformung bringst du alle Terme auf eine Seite

$\Leftrightarrow - \frac{\hbar ^2}{2m} \frac{\partial ^2}{\partial x^2} \psi (x) + V(x) \psi (x) - E \psi (x) = 0$

Nun multiplizierst du mit und klammerst $\psi (x)$ aus

$\frac{\hbar ^2}{2m} \frac{\partial ^2}{\partial x^2} \psi (x) + (E - E_{pot}) \psi (x) = 0$

Zur Vereinfachung wurde hier das Potential V(x) durch die, aus der Schule bekannte Schreibweise für die potentielle Energie $E_{pot}$ , ersetzt.

Jetzt ersetzt du die zweite Ableitung durch die aus der Schule bekannten Form $\frac{\partial ^2}{\partial x ^2} \psi (x)= \psi ^{''} (x)$ und schreibst das reduzierte plancksche Wirkungsquantum aus $\hbar = \frac{h}{2 \pi}$ .

Auf diese Weise erhältst du die Schreibweise wie du sie in vielen Schulbüchern findest

$\frac{h^2}{8 \pi ^2 m} \psi ^{''} (x) + (E-E_{pot}) \psi (x) = 0$

Stationäre Schrödinger Gleichung

im Videozur Stelle im Video springen

(02:27)

Im vorherigen Kapitel hast du bereits den Begriff der stationären Schrödinger Gleichung gelesen. Dabei handelt es sich um einen Spezialfall der Schrödinger Gleichung.

$E \psi = - \frac{\hbar ^2}{2m} \frac{\partial ^2}{\partial x^2} \psi (x) + V(x) \psi (x)$

Sie beschreibt Systeme, bei welchen die Funktionswerte $\psi (x)$ und $E_{pot}$ nur vom Ort, nicht aber von der zeit abhängen. Eine andere Bezeichnung ist auch zeitunabhängig Schrödinger Gleichung.

Schrödinger Gleichung Potentialtopf

Mit der schulphysikalischen Gleichung berechnen wir jetzt ein bekanntes und häufig gesehenes Beispiel, den linearen Potentialtopf.

Die einfache, stationäre Schrödinger Gleichung lautet

$\frac{h^2}{8 \pi ^2 m} \psi ^{''} (x) + (E-E_{pot}) \psi (x) = 0$

Innerhalb des Potentialtopfes mit einer Länge ist die potentielle Energie Null $E_{pot} = 0$ . Die Gesamtenergie entspricht also der kinetischen Energie und vereinfacht unsere Gleichung somit zu

$\psi ^{''} (x) + \frac{8 \pi ^2 m}{h^2} E \psi (x) = 0$

Eine bekannte und mögliche Lösungsfunktion ist die Wellenfunktion für stehende Wellen .

$\psi (x) = \psi _0 \cdot sin \left( \frac{2 \pi x}{\lambda} \right)$

Für diese muss die Bedingung für stehende Wellen mit zwei festen Enden gültig sein.

$L=n \cdot \frac{\lambda}{2}$ und $\lambda = \frac{2 L}{n}$

Setzt du das in die Wellenfunktion ein, erhältst du

$\psi (x) = \psi _0 \cdot sin \left( \frac{\pi x}{L} n \right)$

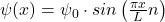
Nun brauchst du noch die zweite Ableitung dieser Funktion. Du erhältst

$\frac{8m}{h^2} \cdot E - \frac{n^2}{L^2} = 0$

Formst du jetzt nach um liefert dir die Gleichung die diskreten Energiewerte des Potentialtopfes.

$E = \frac{h^2}{8mL^2} \cdot n^2$

Die eingesetzte Wellenfunktion ist also eine Lösung der Schrödinger Gleichung.

Schrödinger Gleichung Wasserstoff

im Videozur Stelle im Video springen

(02:43)

Zuletzt betrachte dir die Schrödinger Gleichung des Wasserstoff Atoms. Im Gegensatz zum linearen Potentialtopf gibt es nun drei Raumdimensionen. Damit hängt die Wellenfunktion 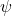$\psi$ nicht mehr nur noch von ab, sondern zudem noch von und .
Zudem bewegt sich das Elektron im elektrischen Potential des Kerns. Damit ist die potentielle Energie nicht Null, sondern hängt vom Abstand des Elektrons zum Kern ab.

Damit ergibt sich für die potentielle Energie in Abhängigkeit vom Abstand folgender Zusammenhang

$E_{pot} = - \frac{e^2}{4 \pi \epsilon_0 r}$

Das ergibt das sogenannte Coulomb-Potential.
Eingesetzt in die Schrödinger Gleichung erhältst du für Wasserstoff

$\psi^{''} (x,y,z) + \frac{8 \pi^2 m_e}{h^2} \left( E + \frac{e^2}{4 \pi \epsilon_0 r} \right) \psi (x,y,z) = 0$

Da die ausführliche Lösung dieses Problems sehr aufwendig ist und den Rahmen dieses Artikels sprengen würde beschränken wir uns hier auf eine Betrachtung der Lösungen.

Das Potential im Wasserstoffatom ist radialsymmetrisch. Somit bietet es sich an die Ortskoordinaten durch Kugelkoordinaten auszudrücken. Dabei wird ein Punkt durch seinen Abstand vom Ursprung und zwei Winkel $\theta$ (Polarwinkel) und $\phi$ (Azimutwinkel) definiert.

Die Koordinaten rechnen sich wie folgt um:

$x = r \cdot sin\theta \cdot cos \phi$

$y = r \cdot sin \theta \cdot \sin \phi$

$z = r \cdot cos \theta$

Für den Grundzustand des Wasserstoffatoms erhältst du die Lösungsfunktion

$\psi_1 = \frac{1}{\sqrt{\pi a^3}} e^{- \frac{r}{a}} \approx 1,47 \cdot 10^{15} e^{- \frac{r}{5,29 \cdot 10^{-11}m}} m^{- \frac{3}{2}}$

Beachte, dass im Nenner des rechten Exponenten der numerische Wert des Bohr’schen Atomradius auftaucht.
Die sich daraus ergebenen Energieniveaus stimmen mit jenen der Bohr’schen Theorie überein.

$E_n = - \frac{13,6 \, eV}{n^2}$

Die Zahl ist die Hauptquantenzahl . Sie kann nur Werte positiver, natürlicher Zahlen einnehmen.

Schrödinger Gleichung — häufigste Fragen

(ausklappen)

Was bedeutet die Wellenfunktion physikalisch?

Die Wellenfunktion $\psi$ beschreibt den quantenmechanischen Zustand eines Teilchens als orts- und zeitabhängige Größe. Aus ihr lässt sich ableiten, wie sich der Zustand mit der Zeit entwickelt, wenn der Energieoperator (Hamilton-Operator) wirkt. Physikalisch gibt $|\psi|^2$ die Wahrscheinlichkeitsdichte für einen Messort an.
Woran erkennt man, ob man die zeitabhängige oder die stationäre Schrödinger-Gleichung benutzen muss?

Die zeitabhängige Schrödinger-Gleichung benutzt man, wenn sich der betrachtete Zustand oder das Potential mit der Zeit ändern kann, also wenn Größen ausdrücklich von abhängen. Die stationäre Schrödinger-Gleichung passt, wenn $\psi$ und das Potential nur vom Ort abhängen und man feste Energiewerte eines Zustands sucht.
Warum gibt es im Potentialtopf nur bestimmte erlaubte Energien und nicht jeden beliebigen Wert?

Im Potentialtopf entstehen nur bestimmte erlaubte Energien, weil die Wellenfunktion an den festen Randpunkten passende Randbedingungen erfüllen muss. Dadurch passen nur bestimmte stehende Wellen in die Länge , also nur bestimmte Wellenlängen. Weil die Energie von dieser Wellenlänge abhängt, werden die Energien diskret.
Was sagt die Hauptquantenzahl beim Wasserstoffatom über den Zustand des Elektrons aus?

Die Hauptquantenzahl kennzeichnet beim Wasserstoffatom das Energieniveau eines Elektronenzustands. Sie kann nur positive natürliche Zahlen annehmen und bestimmt über $E_n = -\frac{13{,}6\,\text{eV}}{n^2}$ , wie stark der Zustand gebunden ist. Größeres bedeutet weniger negative Energie und größere typische Ausdehnung.

Quantenmechanik verstehen

Die Schrödinger-Gleichung ist eine Grundgleichung der Quantenmechanik und beschreibt Teilchen auf atomarer Ebene. Wer sich mit Quantenmechanik beschäftigt, arbeitet mit Wellenfunktionen, Wahrscheinlichkeiten und Energiezuständen statt mit festen Bahnen. So wird klar, warum in vielen Systemen nur bestimmte Energiewerte möglich sind und wie das mit Potenzialen zusammenhängt. Weitere Videos dazu findest du in unserem Ingenieurwissenschaftenbereich.

zur Videoseite: Schrödinger Gleichung