Video anzeigen

Quantenzahlen

Wichtige Inhalte in diesem Video

In diesem Beitrag erklären wir dir, wie die sogenannten Quantenzahlen aussehen und wie du sie vor allem in der Chemie anwenden kannst.

Schau dir gerne unser Video zum Thema an, um den Inhalt dieses Beitrags noch schneller zu verstehen.

Inhaltsübersicht

Quantenzahlen einfach erklärt

zur Stelle im Video springen

(00:10)

Mit den Quantenzahlen kannst du bestimmte, messbare Eigenschaften eines Teilchens, eines Systems oder einem seiner Zustände beschreiben. Sie gehören zum Bereich der Quantenmechanik, der Atomphysik und der Teilchenphysik.

Du kannst den Eigenzustand eines Elektrons und seiner Wellenfunktion in einem Wasserstoffatom durch 4 Quantenzahlen beschreiben. Im Gegensatz zu vielen Größen der klassischen Mechanik, kann eine Quantenzahl nur bestimmte, diskrete Werte annehmen.

Neben diesen 4 Quantenzahlen existieren auch weitere Quantenzahlen für z.B. Mehrelektronensysteme.

Quantenzahlen im Wasserstoffatom

zur Stelle im Video springen

(00:36)

Um ein Wasserstoffatom vollständig zu beschreiben, benötigst du 4 Quantenzahlen. Durch diese kannst du die Eigenzustände des gebundenen Elektrons und seiner Wellenfunktion im Wasserstoff bestimmen. Du kannst dir einen Eigenzustand als einen Zustand eines Systems vorstellen, in dem die Größen genau definierte Werte besitzen.

Diese 4 Quantenzahlen sehen als Zustandsvektor so aus:

$|\psi \rangle = |n, l, m_l, m_s \rangle$

Dabei ist es unmöglich, dass 2 Elektronen innerhalb eines Atoms in allen 4 Zahlen übereinstimmen können. Diese Regel kannst du auch als Pauli-Prinzip bezeichnen.

Hauptquantenzahl

Die Hauptquantenzahl n gibt dir die Schale im Atom an, auf der sich das Elektron befindet. Diese geben gleichzeitig auch das Energieniveau des Elektrons an. Die Schalen werden aufsteigend mit Großbuchstaben bezeichnet: K, L, M, N, O, … . Jede einzelne Schale kann dabei eine bestimmte Anzahl an Elektronen aufnehmen.

Schau dir gerne unseren Beitrag zum Schalenmodell an, um genauere Informationen über die Bedeutung der Schalen zu erhalten.

Die Hauptquantenzahl n kann dabei natürliche Zahlenwerte annehmen:

n = 1, 2, 3, ...

Bei einem Wert von 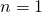n = 1 befindet sich das Elektron also auf der K-Schale und hat das geringste Energieniveau.

Bei einem sehr großen kannst du das zugehörige Atom als Rydberg-Atom bezeichnen.

Das Energieniveau kannst du mit der Hauptquantenzahl durch folgende Formel rechnerisch bestimmen:

$E_{n}=-{\frac {me^{4}}{8\varepsilon _{0}^{2}h^{2}}}\cdot {\frac {1}{n^{2}}}=-E_{\mathrm {R} }{\frac {1}{n^{2}}}$

Das E_R ist die sogenannte Rydberg-Energie. Sie beträgt ungefähr 13,6 eV .

Nebenquantenzahl

Die Nebenquantenzahl wird auch Drehimpulsquantenzahl oder Bahndrehimpulsquantenzahl genannt. Sie gibt dir die Form des Orbitals in einem Atom an. Ein Orbital kannst du dir als einen Raum vorstellen, in dem sich die Elektronen wahrscheinlich aufhalten.

Mehr zu den verschiedenen Orbitalen findest du in unserem Beitrag zum Orbitalmodell .

Die Nebenquantenzahl ist immer kleiner als die Hauptquantenzahl . Sie nimmt, wie auch die Hauptquantenzahl, nur natürliche Werte an. Zusätzlich dazu kann sie auch den Wert 0 annehmen:

l = 0, 1, 2, ... < n

Um Verwechslungen mit der Hauptquantenzahl zu vermeiden, kannst du statt den Zahlen auch Buchstaben zur Beschreibung verwenden:

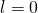mit
mit
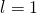mit
mit
mit
Und dann entsprechend dem Alphabet weiter.

Magnetische Quantenzahl

Die magnetische Quantenzahl m_l oder auch Magnetquantenzahl gibt dir an, wie der Elektronen-Bahndrehimpuls räumlich orientiert ist. Die Größe der -Komponente des Elektronen-Bahndrehimpulses ist in der Einheit von $\hbar$ . Das $\hbar$ bezeichnet hierbei das reduzierte plancksche Wirkungsquantum .

Der Name Magnetquantenzahl kommt daher, dass sie die potentielle Energie des Elektrons beschreibt, die man durch Anlegen eines magnetischen Feldes in -Richtung erhält.

Sie kann den Wertebereich von m_l=-l, -(l-1),...-1,0,1,...,(l-1),l annehmen.

Bei einem Wert von m_l = 0 ist die -Komponente des Bahndrehimpulses ebenfalls und hat keinen Einfluss auf die Energie des Elektrons.
Ein Wert von $m_l = \pm l$ bezeichnet die maximal mögliche parallele oder antiparallele Ausrichtung zur -Achse.

Spinquantenzahl

Die Spinquantenzahl beschreibt die Orientierung des Spins zur -Achse.

Der Spin eines Elektrons hat nur zwei mögliche Quantenzustände. Diese sind einmal „linksdrehend“ und einmal „rechtsdrehend„. Deshalb kann die Spinquantenzahl Werte von $s = \pm \frac {1}{2}$ annehmen. Also hat auch die -Komponente nur zwei mögliche Werte:

$s_z = \pm \frac {1}{2} \hbar$

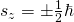
Die magnetische Spinquantenzahl gibt dir dann die Orientierung des Spins zur -Achse an:

$m_s= \frac{s_z}{\hbar}= \pm \frac{1}{2}$

Wie du siehst nimmt sie die gleichen Werte an wie die klassische Spinquantenzahl.

Weitere Quantenzahlen

zur Stelle im Video springen

(03:58)

Neben den 4 Quantenzahlen zur Beschreibung des Elektrons in einem Wasserstoffatom existieren auch noch weitere Quantenzahlen.

Nachfolgend beschreiben wir dir die wichtigsten Beispiele davon.

Gesamtdrehimpulsquantenzahl

Mit der Gesamtdrehimpulsquantenzahl 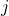kannst du den Gesamtdrehimpuls eines Elektrons beschreiben. Diesen kannst du dir als die Summe der Drehimpulse eines Elektrons vorstellen.

Diese Drehimpulse können z.B. der Bahndrehimpuls (Nebenquantenzahl ) und der Spin (Spinquantenzahl ) sein.
Die Gesamtdrehimpulsquantenzahl ergibt sich nun folgendermaßen:

$j=l+{\tfrac {1}{2}}$

$j=l-{\tfrac {1}{2}},$

Die magnetische Gesamtdrehimpulsquantenzahl m_j kannst du dann so beschreiben:

$m_{j}=[-j,-(j-1),\dots ,j].$

Bei einem Mehrelektronensystem erhältst du dann nochmals neue Quantenzahlen. Der Gesamtbahndrehimpuls und der Gesamtspin gelten jeweils für die Summe der Bahndrehimpulse und der Spins. Die Quantenzahl für den Gesamtdrehimpuls der Atomhülle erhältst du dann durch:

J = L + S und |J = L - S|

Diese Kopplung von Gesamtbahndrehimpuls und Gesamtspin wird auch als LS-Kopplung bezeichnet.

Mehr zur LS-Kopplung und zu den sogenannten Hundschen Regeln findest du in unserem zugehörigen Beitrag .

Kernspinquantenzahl

Die Kernspinquantenzahl beschreibt den Drehimpuls von Atomkernen. Dieser setzt sich aus den Spins und den Bahndrehimpulsen der Protonen und Neutronen innerhalb des Kerns zusammen.

Er kann folgende Werte annehmen:

Ganzzahlige Werte, wenn die Anzahl der Nukleonen (= Protonen und Neutronen) gerade ist z.B. $I({}^{14}\mathrm {N} )=1$
Halbzahlige Werte, wenn die Anzahl der Nukleonen ungerade ist, z.B. $I({}^{1}\mathrm {H} )=1/2.$

Quantenzahlen Chemie

zur Stelle im Video springen

(03:05)

Die Quantenzahlen spielen nicht nur in der Quantenmechanik, sondern auch in den verschiedensten chemischen Zusammenhängen eine wichtige Rolle.

Elektronenkonfiguration

Besonders wichtig in der Chemie ist die sogenannte Elektronenkonfiguration. Diese gibt an, wie die Elektronen in der Elektronenhülle eines Atoms verteilt sind. Mithilfe der Quantenzahlen kannst du die Besetzung der einzelnen Schalen genauer bestimmen.

Mehr zur Elektronenkonfiguration findest du in unserem zugehörigen Beitrag .

Ionisierungsenergie

Die Ionisierungsenergie ist der Energiebeitrag, den du aufwenden musst, um ein Elektron aus der Valenzschale eines Atoms zu lösen. Innerhalb einer Periode des Periodensystems haben dabei alle „neu“ hinzukommenden Elektronen dieselbe Hauptquantenzahl und sitzen in derselben Schale.

Quantenphysik

Quantenmechanik

Quantenzahlen

Quantenzahlen einfach erklärt