Video anzeigen

Compton Effekt

Wichtige Inhalte in diesem Video

Compton Effekt einfach erklärt

(00:12)

Compton Streuung Versuch

(00:52)

Compton Wellenlänge

(01:54)

Compton Effekt Anwendungen

(03:39)

Was ist der Compton Effekt und was hat er mit der Streuung von Photonen zu tun hat? Das erfährst du im Video und hier im Beitrag!

Inhaltsübersicht

Compton Effekt einfach erklärt

im Videozur Stelle im Video springen

(00:12)

Mit dem Compton Effekt beschreibst du die Wechselwirkung zwischen einer Strahlung und Atomen. Genauer gesagt: Wenn Photonen in einem bestimmten Winkel auf ein Elektron treffen, werden sie gestreut. Dabei vergrößert sich ihre Wellenlänge.

Das liegt daran, dass das Photon beim Auftreffen auf das Elektron einen Teil seiner Energie abgibt. Dadurch verliert das Photon Energie und seine Wellenlänge wird größer. Das Elektron besitzt nun die Energie des Photons und wird weggestoßen. Du sagst auch gestreut. Deshalb nennst du diesen Effekt auch Compton Streuung.

Compton Effekt, compton Streuung, compton effekt röntgen — Der Compton Effekt

Merke: Der Compton-Effekt oder Compton-Streuung ist ein Prozess, bei dem die Wellenlänge λ von Photonen beim Auftreffen auf (quasi-)freie Elektronen vergrößert wird. Dabei geben Photonen einen Teil ihrer Energie an die Elektronen ab.

Compton Streuung Versuch

im Videozur Stelle im Video springen

(00:52)

Der Physiker Arthur Holly Compton führte 1923 ein Experiment durch, bei dem er den Compton Effekt entdeckte. Dafür bestrahlte er Graphit mit Röntgenstrahlung (Photonen) und untersuchte die Wellenlänge der gestreuten Strahlung bei unterschiedlichen Einstrahlwinkeln.

Compton ging davon aus, dass die Wellenlänge der Protonen vor und nach der Streuung gleich ist. Jedoch stellte er fest, dass die gestreute Strahlung unterschiedliche Wellenlängen hat. Zum Teil bestand die gestreute Strahlung aus Teilen von:

den ursprünglichen Wellenlängen λ,
und größeren Wellenlängen λ‘.

Das heißt, dass ein Teil der Photonen (der Strahlung) Energie verloren haben müssen.

Über den Anteil der ursprünglichen und größeren Wellenlängen der Streustrahlung konnte Compton auch weitere Beobachtungen machen:

Der Unterschied der Wellenlängen λ‘ – λ wurde größer, je größer der Einfallswinkel $\vartheta$ der Photonen war. Der Anteil der Strahlung mit größerer Wellenlänge λ‘ nimmt also mit größer werdendem Einfallswinkel zu.
Bei unterschiedlichen bestrahlten Elementen bleibt der Unterschied der größeren und der ursprünglichen Wellenlängen λ‘ – λ gleich.
Der Anteil der ursprünglichen Wellenlängen λ in der Streustrahlung nimmt zu, je höher die Ordnungszahl des jeweiligen Elements ist.

Compton Effekt Deutung

Aus seinem Experiment hat Compton gedeutet, dass die Strahlen der Wellenlänge λ entweder auf Elektronen der äußersten Atomhülle treffen oder auf Elektronen, die sich näher am Atomkern befinden. Je nachdem, auf welches sie trifft, ist das Ergebnis des Experiments unterschiedlich.

Auf der äußersten Atomhülle wird das Elektron nur schwach vom Atomkern angezogen. Du bezeichnest es auch als quasifreies Elektron. Durch das Auftreffen des hochenergetischen Photons, wird das Elektron aus der Atomhülle geschleudert. Dabei gibt das Photon einen Teil seiner Energie an das Elektron ab. Dadurch besitzt das Photon nach dem Auftreffen weniger Energie und eine größere Wellenlänge λ‘. Das bezeichnest du auch als vollelastischen Stoß zwischen Photon und Elektron.

Photonen können allerdings auch auf Elektronen treffen, die sich näher am Atomkern befinden. Hier sind die Anziehungskräfte zwischen Elektron und Atomkern stärker. Dadurch wird das Elektron nicht aus der Atomhülle herausgelöst. Beim Auftreffen verliert das Photon außerdem kaum Energie. So kannst du dir erklären, dass die Streustrahlung auch einen deutlich höheren Strahlenanteil der Wellenlänge λ hat.

Compton Wellenlänge

im Videozur Stelle im Video springen

(01:54)

Beim Auftreffen vom Photon auf das Elektron ist der Winkel $\vartheta$ entscheidend. Wenn das Photon das Elektron nur streift ( $\vartheta$ = 0°), behält das Photon fast seine ganze Energie. Bei einem frontalen Zusammenstoß hingegen ( $\vartheta$ = 180°), wird das Photon zurückgeworfen und gibt dabei fast seine ganze Energie an das Elektron ab.

Weil sich durch den Energieverlust die Wellenlänge erhöht, ist der Streuwinkel also nur vom Auftreffwinkel und nicht von der Energie des Photons abhängig. Das berücksichtigst du in der Formel zur Berechnung der Wellenlängenänderung:

$\Delta\lambda=\frac{h}{m_{0}\cdot c}\cdot(1-cos\vartheta)=\lambda_{c}\cdot(1-cos\vartheta)$

Δλ steht für die Wellenlängenänderung des Photons
h ist das Planksche Wirkungsquantum
m₀ ist die Elektronenmasse
c steht für die Lichtgeschwindigkeit
$\vartheta$ ist der Streuwinkel

Compton Effekt, Compton-Effekt, Compten Wellenlänge, Compton-Wellenlänge, Elektron, Photon, Elastischer Stoß, Energie, Impuls — Compton Effekt Beispiel

Bei einem Streuwinkel von $\vartheta$ = 90° kommt es zur sogenannten Compton Wellenlänge λ_C des Elektrons. Dadurch gilt für λ_C(Elektron): $\frac{h}{m_{0}\cdot c}=2,43\cdot10^{-12}\text{m}$

Compton Effekt Herleitung

Für die theoretische Herleitung des Compton Effekts nehmen wir an, dass es sich um ein freies, ruhendes Elektron handelt.

Zunächst brauchst du den Impuls vor () und nach ( $p^{'}$ ) der Streuung.

$p = \frac{E}{c}$

$p^{'} = \frac{E^{'}}{c}$

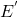Hierbei ist die Photonenenergie vor der Streuung und $E^{'}$ die Energie nach der Streuung. Mit bezeichnest du die Lichtgeschwindigkeit.

Als Nächstes brauchst du die relativistische Energie-Impuls-Beziehung.

$(E^{'}_e)^2 = (E_e)^2 + c^2 \cdot (p^{'}_e)²$

Das kleine zeigt, dass es sich um die Energie des Elektrons handelt. Diese Formel stellst du nach $(p^{'}_e)^2$ um.

$(p^{'}_e)^2 = \frac{(E^{'}_e)^2 - (E_e)^2}{c²}$

Im nächsten Schritt setzt du deine Formeln in den Impulserhaltungssatz ein.

$(p^{'}_e)^2 = p^2 + p^{{'} \, 2} - 2 p \cdot p^{'} \cdot cos \theta$

Hier setzt du deine Formeln ein und löst die Klammern auf.

$\frac{(E^{'}_e)^2 - (E_e)^2}{c^2} = \frac{E^2}{c^2} + \frac{E^{{'} \, 2}}{c^2} - 2 \cdot \frac{E \cdot E^{'}}{c^2} \cdot cos \theta$

Dieser Ausdruck wird dann mit c^2 multiplizieren.

$(E^{'}_e)^2 - (E_e)^2 = E^2 + E^{{'} \, 2} - 2 \cdot E \cdot E^{'} \cdot cos \theta$

Für die weitere Herleitung brauchst du den Energieerhaltungssatz .

$E + E_e = E^{'} + E^{'}_e$

Stelle ihn nach $E^{'}_e$ um.

$E^{'}_e = E+E_e-E^{'}$

Diesen Ausdruck setzt du dann in deine Formel ein und formst ihn um.

$\frac{1}{E^{'}} - \frac{1}{E} = \frac{1}{E_e} \cdot (1- cos \theta)$

Für die Energie des Photons gilt folgender Zusammenhang:

$E = \frac{h \cdot c}{\lambda}$

$E^{'} = \frac{h \cdot c}{\lambda^{'}}$

Zusammen mit $E_e = m_e \cdot c^2$ erhältst du nach Einsetzen und Umformen:

$\Delta\lambda = \frac{h}{m_e \cdot c} \cdot (1-cos \theta)$

Hier setzt du dann deine Compton Wellenlänge $\lambda_{c}$ ein.

$\Delta\lambda = \lambda_C \cdot (1-cos \theta)$

Compton Effekt Anwendungen

im Videozur Stelle im Video springen

(03:39)

Der Compton Effekt hat wichtige praktische Anwendungen in der Wissenschaft und der Medizin.

So setzte die NASA zwischen 1991 und 2000 das Compton Teleskop COMPTEL ein. Es erforschte den Sternenhimmel im Energiebereich zwischen 0,75 und 30 MeV (Mega-Elektronenvolt). Mit den Erkenntnissen war es möglich, Himmelskarten zu erstellen und neue Erkenntnisse der Nukleosynthese zu gewinnen.

Des Weiteren ist die räumliche Auflösung von Compton Kameras deutlich besser als die der heutigen Szintigrafie-Gammakameras. Damit wird zum Beispiel die Lokalisierung von Tumoren und Metastasen wesentlich exakter.

E = mc²

In der Formel zur Berechnung der Wellenlängenänderung durch den Compton Effekt ist dir bereits die Lichtgeschwindigkeit c begegnet. Sie spielt auch in dem Naturgesetz E = mc², das von Albert Einstein entwickelt wurde, eine wichtige Rolle. Wie die Lichtgeschwindigkeit genau mit den anderen Größen zusammenhängt, findest du in unserem Video dazu heraus!