De Broglie Wellenlänge
Wenn du dich fragst, was die de Broglie Wellenlänge von Materiewellen ist und wie sie mit der Wellenlänge von Photonen zusammenhängt, dann findest Du hier alles Wissenswerte dazu übersichtlich zusammengestellt.
In unserem Video haben wir nochmals alles Wichtige zum Thema de Broglie Wellenlänge für Dich aufbereitet.
Inhaltsübersicht
De Broglie Wellenlänge einfach erklärt
Die de Broglie Wellenlänge ist eine quantenmechanische Eigenschaft von Materieteilchen mit endlicher Ruhemasse, also zum Beispiel Elektronen oder Protonen. Sie erklärt sich dadurch, dass Materieteilchen bezüglich ihres Teilchen- und Wellencharakters analog zu Photonen betrachtet werden müssen.
Wie wir zum Beispiel aus Experimenten zum Doppelspalt und zum Photoeffekt wissen, verhält sich elektromagnetische Strahlung, wie beispielsweise Licht, nicht nur wie eine Welle, sondern gleichzeitig auch wie ein Strahl einzelner Teilchen mit diskreter Energie, sogenannter Photonen. Photonen zeigen also sowohl Welleneigenschaften als auch Eigenschaften klassischer (Punkt-)Teilchen. Dieses Phänomen nennt man den Welle-Teilchen-Dualismus.
Der Physiker Louis de Broglie übertrug das Prinzip des Welle-Teilchen Dualismus von Photonen, die masselos sind und sich mit Lichtgeschwindigkeit bewegen, auf massebehaftete Materieteilchen mit Geschwindigkeiten kleiner als die Lichtgeschwindigkeit. So wie Lichtwellen also ebenso den Teilchencharakter besitzen, verhalten sich im Gegenzug Materieteilchen auch wie Wellen.
Diese Wellen nennt man Materiewellen und ihre Wellenlänge ist die de Broglie Wellenlänge  .
.
De Broglie Wellenlänge klassischer Fall
Im nicht-relativisischen Fall können wir die de Broglie Wellenlänge  über die folgende Formel berechnen
über die folgende Formel berechnen
 .
.
Dabei ist  das Plancksche Wirkungsquantum und
das Plancksche Wirkungsquantum und  der Impuls
des Teilchens. Dementsprechend sind
der Impuls
des Teilchens. Dementsprechend sind  seine (Ruhe-)Masse und
seine (Ruhe-)Masse und  seine Geschwindigkeit.
seine Geschwindigkeit.  ist die kinetische Energie
.
ist die kinetische Energie
.
Im Falle eines Teilchens mit elektrischer Ladung  , das von einer konstanten Beschleunigungsspannung
, das von einer konstanten Beschleunigungsspannung  beschleunigt wird, wie zum Beispiel in einem Plattenkondensator
, gilt
beschleunigt wird, wie zum Beispiel in einem Plattenkondensator
, gilt  und wir erhalten
und wir erhalten
 .
.
Betrachten wir hingegen Teilchen in einem idealen Gas mit der Temperatur  , so ist die mittlere thermische Energie der Teilchen
, so ist die mittlere thermische Energie der Teilchen  und wir berechnen die sogenannte thermische de Broglie Wellenlänge
und wir berechnen die sogenannte thermische de Broglie Wellenlänge
 .
.
De Broglie Wellenlänge relativistischer Fall
Falls eine relativistische Rechnung nötig ist, können wir zur Bestimmung der relativistischen de Broglie Wellenlänge  dieselbe Formel nutzen, müssen aber den relativistischen Impuls
dieselbe Formel nutzen, müssen aber den relativistischen Impuls  verwenden
verwenden
 .
.
Dabei ist  der Lorentz Faktor
der Lorentz Faktor

mit der Lichtgeschwindigkeit  . Es gilt stets
. Es gilt stets  , da
, da  .
.
De Broglie Wellenlänge Interpretation
Es ist schwierig, eine gute Intuition für den Welle-Teilchen-Dualismus und Materiewellen zu gewinnen. Du darfst Dir unter Materiewellen trotz des Namens keinesfalls echte Wellen schwingender Materie, ein Teilchen auf einer Wellenbahn oder Ähnliches vorstellen. Am besten sollte man gar nicht erst versuchen, sich den Wellencharakter von Teilchen bildlich vorzustellen. Die mikroskopischen Quantenobjekte entziehen sich hier einfach unserer Vorstellungskraft, die nunmal auf unsere makroskopische Lebenswelt geeicht ist. Letzendlich haben wir es einfach mit (Punkt-)Teilchen zu tun, die gleichzeitig Eigenschaften einer Welle zeigen. Mal zeigen sie die einen, mal die anderen Eigenschaften, je nachdem wie sie gerade interagieren.
In der klassischen Physik spielt die de Broglie Wellenlänge von Materie keine Rolle. Das werden wir später in einer Beispielrechnung sehen.
De Broglie Wellenlänge Herleitung
Wie bereits besprochen erklären sich Materiewellen dadurch, dass wir fordern, dass der für Photonen gültige Welle-Teilchen-Dualismus auch für Materieteilchen gilt. Beginnen wir für die Herleitung der Formel für die de Broglie Wellenlänge also bei Photonen und leiten daraus in einem ersten Schritt die klassischen Formeln her. Mit diesen finden wir dann ihre relativistische Verallgemeinerung.
Herleitung klassischer Fall
Eine elektromagnetischen Welle der Frequenz  beziehungsweise der Wellenlänge
beziehungsweise der Wellenlänge  lässt sich über Photonen der Energie
lässt sich über Photonen der Energie

beschreiben. Und obwohl Photonen keine Ruhemasse haben, kann ihnen doch ein Impuls

zugeordnet werden. Diese Beziehung zwischen Wellenlänge und Impuls verwenden wir nun, gemäß dem Welle-Teilchen-Dualismus, auch für Materiewellen und erhalten die Formel für die de Broglie Wellenlänge
 .
.
Auch die Frequenz der Materiewelle (nennen wir sie  zur Unterscheidung von der Photonenfrequenz
zur Unterscheidung von der Photonenfrequenz  ) können wir mit der Formel für Photonen bestimmen. Dabei setzen wir für die Energie die kinetische Energie des Teilchens ein und erhalten
) können wir mit der Formel für Photonen bestimmen. Dabei setzen wir für die Energie die kinetische Energie des Teilchens ein und erhalten

Diese Relation zwischen Frequenz und inverser Wellenlänge ist im Gegensatz zu Licht/Photonen nicht linear, sondern quadratisch!
Herleitung relativistischer Fall
Zur relativistischen Verallgemeinerung der de Broglie Wellenlänge verwenden wir zwei grundlegende Formeln der Relativitätstheorie: Einsteins Formel zur Äquivalenz von Masse und Energie und die relativistische Energie-Impuls-Beziehung. Einsteins Formel ist die bekannte Gleichung für die Gesamtenergie eines relativistischen Teilchens
 ,
,
wobei 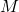 die geschwindigkeitsabhängige relativistische Masse bezeichnet. Sie hängt mit der Ruhemasse
die geschwindigkeitsabhängige relativistische Masse bezeichnet. Sie hängt mit der Ruhemasse  wie folgt zusammen
wie folgt zusammen
 .
.
Beachte, dass stets gilt  . Für
. Für  reduziert sich dementsprechend die Gesamtenergie auf die konstante Ruheenergie:
reduziert sich dementsprechend die Gesamtenergie auf die konstante Ruheenergie:  .
.
Die Energie-Impuls-Beziehung zwischen der Gesamtenergie und dem relativistischen Impuls lautet
 .
.
Mit diesen beiden Formeln können wir den relativistischen Impuls berechnen

Setzen wir den relativistischen Impuls in die Formel für die klassische de Broglie Wellenlänge ein, finden wir ihre relativistische Version

Alternativ können wir  auch wie folgt angeben
auch wie folgt angeben

und die relativistische de Broglie Wellenlänge damit bestimmen
 .
.
Die Grenze für nicht-relativistische Rechnungen wählt man meist bei  beziehungsweise
beziehungsweise  .
.
De Broglie Wellenlänge berechnen
Jetzt wollen wir die de Broglie Wellenlänge für zwei einfache Systeme berechnen. Sehen wir uns zuerst einen laufenden Menschen – wir wollen ihn als Punktteilchen nähern – mit  und
und  an. Wenn wir diese Werte in die bekannte Formel einsetzen erhalten wir
an. Wenn wir diese Werte in die bekannte Formel einsetzen erhalten wir

Wir sehen also, dass der Wellencharakter von Materie in der klassischen Mechanik komplett irelevant ist und wir ihn vernachlässigen können.
Für Quantenteilchen spielt die de Broglie Wellenlänge jedoch eine wichtige Rolle. Betrachten wir dafür als zweites ein Proton mit Masse  und Ladung
und Ladung  in einem Plattenkondensator mit der Beschleunigungspannung
in einem Plattenkondensator mit der Beschleunigungspannung  . Nach Durchlauf des Kondensators gilt dann
. Nach Durchlauf des Kondensators gilt dann

Das ist mehr als der Protonenradius von ca.  ! Wir können ein solches Proton also nicht als reines Teilchen behandeln.
! Wir können ein solches Proton also nicht als reines Teilchen behandeln.
De Broglie Wellenlänge Experimenteller Nachweis
Es gibt viele Möglichkeiten, den Wellencharakter von Materie experimentell zu überprüfen. Eine davon ist der Nachweis mittels Beugungsexperimenten an Kristallen .
Präparieren wir hierzu eine Elektronenemitter so, dass ein Strahl aus Elektronen mit großen zeitlichen Abständen erzeugt wird (es sind also immer nur einzelne Elektronen „unterwegs“). Wenn wir mit diesem Strahl jetzt ein Beugungsexperiment durchführen und die einzelnen ausgehenden Elektronen detektieren, wird sich mit der Zeit und mit zunehmender Zahl an Elektronen das bekannte Beugungsmuster bilden; ganz so wie wir es von einer elektromagnetischen Welle erwarten würden. Gleichzeitig besteht der Elektronenstrahl aber nur aus einzelnen Elektronen. Dieses Ergebnis lässt sich nur dadurch erklären, dass das Elektron gleichzeitig Teilchen und Welle ist.
De Broglie Wellenlänge bei verschiedenen Beschleunigungsspannungen
Im Folgenden sind noch einige Werte für die de Broglie Wellenlängen von Elektronen ( ,
,  ) und Protonen bei wachsenden Beschleunigungsspannungen angegeben. Im relativistischen Bereich von Elektronen (bei
) und Protonen bei wachsenden Beschleunigungsspannungen angegeben. Im relativistischen Bereich von Elektronen (bei  haben wir für Elektronen bereits
haben wir für Elektronen bereits  und bei
und bei  schon
schon  ) nimmt die de Broglie Wellenlänge mit wachsender Energie wesentlich langsamer ab. Protonen sind aufgrund ihrer höheren Masse bei diesen Spannungen noch nicht relativistisch.
) nimmt die de Broglie Wellenlänge mit wachsender Energie wesentlich langsamer ab. Protonen sind aufgrund ihrer höheren Masse bei diesen Spannungen noch nicht relativistisch.
| Beschleunigungsspannung U | de Broglie Wellenlänge Elektron | de Broglie Wellenlänge Proton |
| 10 V | λdB = 3,88 • 10-10 m | λdB = 9,07 • 10-12 m |
| 100 V | λdB = 1,23 • 10-10 m | λdB = 2,87 • 10-12 m |
| 1.000 V | λdB = 3,88 • 10-11 m | λdB = 9,07 • 10-13 m |
| 10.000 V | λdB(rel) = 1,22 • 10-11 m | λdB = 2,87 • 10-12 m |
| 100.000 V | λdB(rel) = 3,71 • 10-12 m | λdB = 9,07 • 10-14 m |
| 1.000.000 V | λdB(rel) = 8,74 • 10-13 m | λdB = 2,87 • 10-14 m |