Lineare Unabhängigkeit und lineare Abhängigkeit
Lineare Unabhängigkeit und Lineare Abhängigkeit ist ein zentrales Thema der linearen Algebra. Du solltest es daher zu einhundert Prozent verstanden haben. Wir erklären es dir mit einfachen Beispielen und Bildern.
Du möchtest dich ein bisschen zurücklehnen und nicht den ganzen Text zur linearen Abhängigkeit und linearen Unabhängigkeit lesen? Kein Problem! Dann schau dir am besten unser kurzes Video an!
Inhaltsübersicht
Lineare Unabhängigkeit und lineare Abhängigkeit einfach erklärt
Untersuchst du zwei Vektoren auf Lineare Abhängigkeit oder lineare Unabhängigkeit, so erfährst du, wie sie im Vektorraum zueinander stehen. Du kannst somit direkt erkennen, ob sie in dieselbe Richtung zeigen (lineare Abhängigkeit), oder beispielsweise eine Ebene im  aufspannen (lineare Unabhängigkeit).
aufspannen (lineare Unabhängigkeit).
Betrachtest du mehrere Vektoren, so kann es vorkommen, dass du nicht alle benötigst, um den kompletten Vektorraum aufzuspannen. Dann sind diejenigen Vektoren, die den Raum aufspannen linear unabhängig, insgesamt ist die Familie der Vektoren jedoch linear abhängig.
Lineare Abhängigkeit von Vektoren
Hier wird dir die lineare Abhängigkeit erst anhand von zwei beziehungsweise drei Vektoren erklärt, im dritten Unterpunkt findest du das allgemeine Verfahren, um Vektoren auf lineare Abhängigkeit zu prüfen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Lineare Abhängigkeit von 2 Vektoren
Gegeben sei ein Vektorraum V
, der die zwei Vektoren  und
und  enthält. Wichtig ist, dass keiner der Nullvektor ist.
enthält. Wichtig ist, dass keiner der Nullvektor ist.  und
und  sind genau dann linear abhängig, wenn sie parallel sind. Je nach Vektorraum kann es schwierig sein, die Vektoren zu zeichnen. Deswegen wollen wir lineare Abhängigkeit auch algebraisch bestimmen.
sind genau dann linear abhängig, wenn sie parallel sind. Je nach Vektorraum kann es schwierig sein, die Vektoren zu zeichnen. Deswegen wollen wir lineare Abhängigkeit auch algebraisch bestimmen.
Lineare Abhängigkeit zweier Vektoren ist gegeben, wenn einer das Vielfache des anderen Vektors ist. Mathematisch bedeutet das für ein 

Lineare Abhängigkeit von 3 Vektoren
Bei drei Vektoren ist die lineare Abhängigkeit schon etwas schwieriger zu zeigen. Hier nennen wir die drei Vektoren 
 und
und  linear abhängig, wenn sich einer als Linearkombination der anderen beiden darstellen lässt. Das bedeutet, es existieren
linear abhängig, wenn sich einer als Linearkombination der anderen beiden darstellen lässt. Das bedeutet, es existieren  und
und  , sodass
, sodass

Beispiel
Die drei Vektoren  ,
,  ,
,  und sind linear abhängig. Das siehst du direkt, wenn du
und sind linear abhängig. Das siehst du direkt, wenn du  und
und  wählst
wählst

Du kannst also den Vektor  darstellen, indem du die Vektoren
darstellen, indem du die Vektoren  und
und  mit einer bestimmten Zahl multiplizierst.
mit einer bestimmten Zahl multiplizierst.
Drei Vektoren im  sind immer linear abhängig. Analog sind vier Vektoren im
sind immer linear abhängig. Analog sind vier Vektoren im  immer linear abhängig. Das liegt daran, dass drei Vektoren ausreichen, um den ganzen
immer linear abhängig. Das liegt daran, dass drei Vektoren ausreichen, um den ganzen  aufzuspannen.
aufzuspannen.
Lineare Abhängigkeit von Vektoren allgemein
Obige Aussagen lassen sich leicht verallgemeinern. Wir definieren lineare Abhängigkeit für  verschiedene Vektoren
verschiedene Vektoren  , wenn es
, wenn es  gibt, sodass der Nullvektor
gibt, sodass der Nullvektor  als Linearkombination aller
als Linearkombination aller  ,
,  dargestellt werden kann. Es muss also gelten
dargestellt werden kann. Es muss also gelten
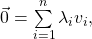
wobei nicht alle  sein dürfen. Alternativ kann man auch sagen, dass
sein dürfen. Alternativ kann man auch sagen, dass  linear abhängig sind, wenn
linear abhängig sind, wenn  mit
mit  als Linearkombination der anderen Vektoren
als Linearkombination der anderen Vektoren  dargestellt werden kann
dargestellt werden kann

Diese Definition siehst du sofort an den Beispielen oben.
- Der Nullvektor ist immer linear abhängig
- Trivialerweise ist
 wenn alle
wenn alle 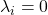 sind. Diesen Fall musst du immer ausschließen, wenn du lineare Abhängigkeit prüfst.
sind. Diesen Fall musst du immer ausschließen, wenn du lineare Abhängigkeit prüfst.
Lineare Unabhängigkeit von Vektoren
Lineare Abhängigkeit kannst du jetzt bestimmen, aber wann sind Vektoren linear unabhängig? Ganz einfach: Lineare Unabhängigkeit ist immer gegeben, wenn die Vektoren nicht linear abhängig sind!
Und wie prüft man das am besten? Das siehst du hier direkt am Beispiel oder formal im nächsten Absatz.
Beispiel 1
Die Vektoren  und
und  sind linear unabhängig, weil für alle
sind linear unabhängig, weil für alle  gilt
gilt

Erhältst du den Nullvektor nur als Linearkombination der Vektoren, wenn alle 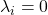 sind, bedeutet das die lineare Unabhängigkeit der Vektoren
sind, bedeutet das die lineare Unabhängigkeit der Vektoren  .
.
Konkret heißt das

Beispiel 2
Wir wollen die Vektoren  ,
,  und
und  auf lineare Unabhängigkeit untersuchen. Wir müssen also zeigen, dass aus
auf lineare Unabhängigkeit untersuchen. Wir müssen also zeigen, dass aus

folgt, dass  ist.
ist.
Im folgenden Abschnitt erfährst du, welche verschiedenen Varianten du dafür verwenden kannst.
Lineare Unabhängigkeit prüfen
Es gibt verschiedene Möglichkeiten, die lineare Unabhängigkeit der Vektoren aus Beispiel 2 nachzurechnen. Zum einen kannst du das zugehörige lineare Gleichungssystem lösen. Das kann je nach Dimension deines Vektorraums etwas ausarten. Schneller geht es mit dem Gaußschen Eliminationsverfahren oder mit der Determinante.
Gleichungssystem lösen
Dazu betrachten wir die Vektoren komponentenweise und lösen das Gleichungssystem:
(I) 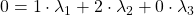
(II) 
(III) 
Aus (II) sehen wir direkt, dass  gelten muss. Einsetzen in (III) liefert uns
gelten muss. Einsetzen in (III) liefert uns  . Damit ist in (I) auch
. Damit ist in (I) auch  . Wir haben lineare Unabhängigkeit gezeigt.
. Wir haben lineare Unabhängigkeit gezeigt.
Gaußsches Eliminationsverfahren
Ein Gleichungssystem explizit auszurechnen, ist je nach Vektorraum und Anzahl der Vektoren etwas mühsam. Leichter und schneller geht es mit dem Gaußschen Eliminationsverfahren . Dazu schreibst du deine Vektoren nebeneinander in eine Matrix und formst sie entsprechend um.
Nullzeile oder -Spalte in der Matrix  Lineare Abhängigkeit der Vektoren
Lineare Abhängigkeit der Vektoren
Keine Nullzeile oder-Spalte in der Matrix  Lineare Unabhängigkeit der Vektoren.
Lineare Unabhängigkeit der Vektoren.
In Beispiel 2 sieht die Matrix folgendermaßen aus:

Wir sehen sofort, dass sich mit dem Gauß Algorithmus keine Nullzeile beziehungsweise Nullspalte erzeugen lässt. Somit sind unsere Vektoren also linear unabhängig.
Elementare Umformungen, wie das Gauschen Eliminationsverfahren, verändern die lineare Abhängigkeit oder lineare Unabhängigkeit nicht.
Determinante
Ergeben deine Vektoren eine quadratische Matrix  , so kannst du die lineare Unabhängigkeit über die Determinate prüfen. Es gilt
, so kannst du die lineare Unabhängigkeit über die Determinate prüfen. Es gilt
 Lineare Abhängigkeit
Lineare Abhängigkeit
 Lineare Unabhängigkeit.
Lineare Unabhängigkeit.
Im Beispiel 2 sieht man direkt, dass  ist, somit haben wir abermals lineare Unabhängigkeit gezeigt.
ist, somit haben wir abermals lineare Unabhängigkeit gezeigt.
Lineare Abhängigkeit und lineare Unabhängigkeit von Matrizen
Nicht nur Vektoren können linear abhängig oder unabhängig sein, sondern alle Elemente, die in einem Vektorraum leben. Betrachten wir also z.B. den Raum aller  -Matrizen
-Matrizen  . Er enthält zum Beispiel die Matrizen
. Er enthält zum Beispiel die Matrizen

Diese sind linear abhängig, da

Wie du siehst, funktioniert lineare Abhängigkeit und lineare Unabhängigkeit hier genauso!
Lineare Abhängigkeit und Lineare Unabhängigkeit: Bedeutung
Jetzt kannst du lineare Abhängigkeit und lineare Unabhängigkeit von Vektoren bestimmen. Doch wozu braucht man das überhaupt? Die vermutlich wichtigste Anwendung ist die Bestimmung einer Basis des Vektorraums. Für eine Basis brauchst du die maximale Anzahl linear unabhängiger Vektoren. Das sind die Vektoren, die du brauchst, um den ganzen Vektorraum aufzuspannen. Das einfachste Beispiel ist hier die Standardbasis des  . Sie besteht aus den Einheitsvektoren, die nur in einem Eintrag eine 1 stehen haben.
. Sie besteht aus den Einheitsvektoren, die nur in einem Eintrag eine 1 stehen haben.
Die Standardbasis des  sieht zum Beispiel so aus:
sieht zum Beispiel so aus:


 und
und  sind linear abhängig, weil für
sind linear abhängig, weil für  gilt
gilt
 ), erhältst du also den Vektor
), erhältst du also den Vektor 
