QR Zerlegung
Im Folgenden erklären wir, was unter einer QR Zerlegung zu verstehen ist und wie man sie berechnet. Dafür stellen wir zwei Verfahren mit Beispielen zur Berechnung vor: die Householdertransformation und das Gram-Schmidt Verfahren.
Wenn du also möglichst schnell lernen möchtest, wie du selbst eine QR Zerlegung bestimmen kannst, dann schau dir unser Video dazu an.
Inhaltsübersicht
QR Zerlegung einfach erklärt
Bei einer QR Zerlegung möchte man eine Matrix  als Produkt zweier Matrizen darstellen, d.h. es soll gelten
als Produkt zweier Matrizen darstellen, d.h. es soll gelten  . Dabei soll
. Dabei soll  eine orthogonale Matrix und
eine orthogonale Matrix und  eine obere Dreiecksmatrix sein.
eine obere Dreiecksmatrix sein.
Die Zeilen und Spalten einer orthogonalen Matrix  stellen eine Orthonormalbasis
des
stellen eine Orthonormalbasis
des  dar, d.h. es gilt für die Transponierte
dar, d.h. es gilt für die Transponierte 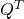 , dass
, dass  der Einheitsmatrix entspricht.
der Einheitsmatrix entspricht.
Bei einer oberen Dreiecksmatrix  , sind alle Einträge unterhalb der Diagonalen Null, d.h. für
, sind alle Einträge unterhalb der Diagonalen Null, d.h. für  gilt
gilt  .
.
Allgemeine QR Zerlegung
Betrachtet man also eine Matrix  mit
mit  , dann besitzt sie eine (fast) eindeutige reduzierte QR Zerlegung. D.h. es existiert eine Matrix
, dann besitzt sie eine (fast) eindeutige reduzierte QR Zerlegung. D.h. es existiert eine Matrix  , deren Spalten orthogonal sind und eine obere Dreiecksmatrix
, deren Spalten orthogonal sind und eine obere Dreiecksmatrix  , sodass
, sodass  . Um nun eine vollständige QR Zerlegung zu erhalten, muss die
. Um nun eine vollständige QR Zerlegung zu erhalten, muss die  -Matrix
-Matrix  durch weitere orthogonale Spalten
durch weitere orthogonale Spalten  zu einer quadratischen
zu einer quadratischen 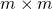 -Matrix
-Matrix  erweitert werden. Damit die Multiplikation weiterhin sinnvoll besteht und
erweitert werden. Damit die Multiplikation weiterhin sinnvoll besteht und  ergibt, erweitern wir
ergibt, erweitern wir 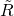 um die entsprechenden Nullzeilen zu
um die entsprechenden Nullzeilen zu  , sodass schließlich
, sodass schließlich
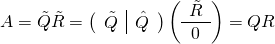
eine vollständige QR Zerlegung darstellt.
Die QR Zerlegung ist eindeutig für eine Matrix  mit
mit  und
und  , wenn vorausgesetzt wird, dass die Diagonalelemente von
, wenn vorausgesetzt wird, dass die Diagonalelemente von  alle positiv oder negativ sein sollen.
alle positiv oder negativ sein sollen.
Wir betrachten nun eine solche  -Matrix mit
-Matrix mit  und
und  und zeigen ein Verfahren zur Berechnung ihrer Zerlegung.
und zeigen ein Verfahren zur Berechnung ihrer Zerlegung.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
QR Zerlegung per Householdertransformation
Die Householdertransformation spiegelt einen Vektor an einer Ebene, die durch den Nullpunkt verläuft. Für die QR Zerlegung nutzen wir das, indem wir Spaltenvektoren auf ein Vielfaches des ersten Einheitsvektors spiegeln, um so Schritt für Schritt eine obere Dreiecksmatrix  zu erhalten. Die lineare Abbildung, welche die Householdertransformation beschreibt, wird durch eine orthogonale Householder-Matrix
zu erhalten. Die lineare Abbildung, welche die Householdertransformation beschreibt, wird durch eine orthogonale Householder-Matrix  dargestellt. Dabei entspricht
dargestellt. Dabei entspricht  dem Vektor, der senkrecht zur Spiegelebene liegt. Im 2-dimensionalen kann man diese Spiegelung folgendermaßen Veranschaulichen.
dem Vektor, der senkrecht zur Spiegelebene liegt. Im 2-dimensionalen kann man diese Spiegelung folgendermaßen Veranschaulichen.
Uns ist nun eine Matrix  gegeben und wir wollen diese durch Householdertransformationen in eine obere Dreiecksmatrix verwandeln. Dafür bestimmen wir Householder-Matrizen
gegeben und wir wollen diese durch Householdertransformationen in eine obere Dreiecksmatrix verwandeln. Dafür bestimmen wir Householder-Matrizen  und multiplizieren diese von links an
und multiplizieren diese von links an  , sodass wir nach höchstens
, sodass wir nach höchstens  Schritten das Resultat
Schritten das Resultat  erhalten. Da die Householder-Matrizen orthogonal sind und das Produkt von orthogonalen Matrizen erneut orthogonal ist, liefert uns eine Linksmultiplikation mit
erhalten. Da die Householder-Matrizen orthogonal sind und das Produkt von orthogonalen Matrizen erneut orthogonal ist, liefert uns eine Linksmultiplikation mit  die gewünschte QR-Zerlegung:
die gewünschte QR-Zerlegung:  . Nun bleibt nur noch zu klären wie genau wir diese Householder-Matrizen berechnen.
. Nun bleibt nur noch zu klären wie genau wir diese Householder-Matrizen berechnen.
Householder-Matrizen berechnen
Schritt 1: Wir betrachten dafür die erste Spalte  unserer Matrix
unserer Matrix  und wählen
und wählen  . Dabei entspricht
. Dabei entspricht  dem Vorzeichen des ersten Eintrags des Spaltenvektors
dem Vorzeichen des ersten Eintrags des Spaltenvektors  und
und  der euklidischen Norm von
der euklidischen Norm von  . Zudem gilt
. Zudem gilt  . Mit dem Vektor
. Mit dem Vektor  bestimmen wir die Householder-Matrix
bestimmen wir die Householder-Matrix  , welche durch Multiplikation mit
, welche durch Multiplikation mit  eine Matrix, wir nennen sie hier
eine Matrix, wir nennen sie hier  , liefert, deren erste Spalte ein Vielfaches des Einheitsvektors ist.
, liefert, deren erste Spalte ein Vielfaches des Einheitsvektors ist.
Schritt 2.1: Im nächsten Schritt nehmen wir diese Matrix  und streichen ihre erste Zeile und Spalte, sodass wir eine kleinere Teilmatrix
und streichen ihre erste Zeile und Spalte, sodass wir eine kleinere Teilmatrix  erhalten.
erhalten.
Schritt 2.2: Wir gehen nun mit 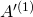 genauso vor, wie mit
genauso vor, wie mit  in Schritt 1. Explizit bedeutet das, wir spiegeln ihre erste Spalte
in Schritt 1. Explizit bedeutet das, wir spiegeln ihre erste Spalte  auf ein Vielfaches des ersten Einheitsvektors
auf ein Vielfaches des ersten Einheitsvektors  . Dafür berechnen wir
. Dafür berechnen wir  , um damit die
, um damit die  -Matrix
-Matrix  zu berechnen. Im Anschluss definieren wir dann unsere
zu berechnen. Im Anschluss definieren wir dann unsere 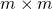 –Householder-Matrix
–Householder-Matrix  durch
durch
 .
.
Nun multiplizieren wir  von links an die zuvor berechnete Matrix
von links an die zuvor berechnete Matrix  . Die daraus resultierende Matrix
. Die daraus resultierende Matrix  hat nun in den ersten beiden Spalten unterhalb dem Eintrag
hat nun in den ersten beiden Spalten unterhalb dem Eintrag  nur Nullen .
nur Nullen .
Schritt 3.1: Um das selbe auch für die restlichen Spalten zu erreichen, streichen wir im nächsten Schritt sowohl die erste und zweite Zeile, als auch Spalte von  und führen Schritt 3.2 analog zu Schritt 2.2 für die Teilmatrix
und führen Schritt 3.2 analog zu Schritt 2.2 für die Teilmatrix  durch und erweitern dann die
durch und erweitern dann die  -Matrix
-Matrix 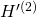 zu
zu
 .
.
Nun berechnen wir  .
.
Diese Schritte führen wir solange fort, bis wir eine obere Dreiecksmatrix erhalten, was spätestens nach Schritt  der Fall ist.
der Fall ist.
QR Zerlegung mit dem Gram-Schmidt Verfahren
Ein weiteres Verfahren für die QR Zerlegung stellt das Verfahren von Gram-Schmidt
dar. Dieses Verfahren erzeugt aus einer gegebenen Basis eine Orthonormalbasis. Inwiefern kann dies bei einer Zerlegung hilfreich sein? Sei  eine Matrix mit
eine Matrix mit  . Demnach sind die Spalten
. Demnach sind die Spalten  allesamt linear unabhängig und stellen deshalb eine Basis des
allesamt linear unabhängig und stellen deshalb eine Basis des  dar. Mit dem Gram-Schmidt Verfahren erzeugen wir daraus eine Orthonormalbasis
dar. Mit dem Gram-Schmidt Verfahren erzeugen wir daraus eine Orthonormalbasis  und erstellen damit eine orthogonale
und erstellen damit eine orthogonale  -Matrix
-Matrix  . Berechnen wir nun das Produkt
. Berechnen wir nun das Produkt  so erhalten wir eine obere Dreiecksmatrix. Denn aufgrund der Konstruktion der orthogonalen Vektoren gilt für alle
so erhalten wir eine obere Dreiecksmatrix. Denn aufgrund der Konstruktion der orthogonalen Vektoren gilt für alle  , dass
, dass  .
.
QR Zerlegung per Householdertransformation
Wir wollen folgende Matrix als Produkt einer orthogonalen und einer oberen Dreiecksmatrix darstellen:
 .
.
Wir betrachten den ersten Spaltenvektor  und berechnen seine Norm
und berechnen seine Norm  . Damit bestimmen wir den orthogonalen Vektor zu unserer Spiegelebene
. Damit bestimmen wir den orthogonalen Vektor zu unserer Spiegelebene
 .
.
Um nun die erste Householder-Matrix  bestimmen zu können, berechnen wir zunächst
bestimmen zu können, berechnen wir zunächst  und
und
 .
.
Damit erhalten wir die Householder-Matrix  :
:
 .
.
Diese Matrix  multiplizieren wir anschließend von links auf
multiplizieren wir anschließend von links auf  :
:

 .
.
Wir streichen die erste Zeile und Spalte von  und erhalten die Teilmatrix
und erhalten die Teilmatrix
 .
.
Nun betrachten wir ihre erste Spalte 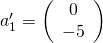 und berechnen erneut die Norm
und berechnen erneut die Norm  . Damit bestimmen wir
. Damit bestimmen wir
 .
.
Daraus ergibt sich die „kleine“ Householder-Matrix

und schließlich bilden wir so die „große“ Householder-Matrix
 .
.
Nun berechnen wir

und erhalten so eine obere Dreiecksmatrix  .
.
Zu guter letzt berechnen wir noch die Transponierte der orthogonalen Matrix:

 .
.
Somit ist  .
.
QR Zerlegung mit dem Gram-Schmidt Verfahren
Wir wollen für folgende Matrix eine QR Zerlegung durchführen:
 .
.
Das bedeutet wir wenden auf die Vektoren  und
und  das Gram-Schmidt Verfahren an und erhalten damit
das Gram-Schmidt Verfahren an und erhalten damit  und
und  . Damit bilden wir nun die orthogonale Matrix
. Damit bilden wir nun die orthogonale Matrix

und berechnen unsere obere Dreiecksmatrix
 .
.
Schließlich gilt damit  .
.
Anwendungen
Die QR Zerlegung wird sehr häufig in der numerischen Mathematik angewandt, beispielsweise im QR-Algorithmus zur Berechnung der Eigenwerte einer Matrix. Es ist aber auch hilfreich beim Lösen linearer Gleichungssysteme.
Lösung regulärer Gleichungssysteme
Gegeben ist ein lineares Gleichungssystem (LGS) in der Matrixform  mit
mit  und
und  . Es gelte
. Es gelte  , weshalb das System genau eine Lösung besitzt. Gesucht ist diese Lösung
, weshalb das System genau eine Lösung besitzt. Gesucht ist diese Lösung  . Um sie zu bestimmen gehen wir folgendermaßen vor:
. Um sie zu bestimmen gehen wir folgendermaßen vor:
- Bestimmung einer QR Zerlegung von
 . (Denn damit lässt sich das LGS zu
. (Denn damit lässt sich das LGS zu  umformulieren.)
umformulieren.) - Berechnung von
 . (Linksmultiplikation von
. (Linksmultiplikation von 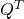 im LGS führt zu
im LGS führt zu  .)
.) -
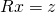 durch Rückwärtseinsetzen lösen.
durch Rückwärtseinsetzen lösen.
Lösung unbestimmter Gleichungssysteme
Gegeben sei ein LGS wie oben, mit dem Unterschied, dass  und
und  gilt. Zur Lösung des LGS gehen wir folgendermaßen vor:
gilt. Zur Lösung des LGS gehen wir folgendermaßen vor:
- Bestimmung einer QR Zerlegung von
 . (Damit ergibt sich das LGS
. (Damit ergibt sich das LGS  .)
.) -
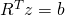 durch Vorwärtseinsetzen lösen. (
durch Vorwärtseinsetzen lösen. ( )
) - Berechnung von
 .
.
