Vereinigungsmenge
Du möchtest wissen, was eine Vereinigungsmenge ist und wie du sie berechnen kannst? Hier und in unserem Video erfährst du es!
Inhaltsübersicht
Was ist eine Vereinigungsmenge?
Die Vereinigungsmenge verstehst du am besten an einem Beispiel. Stell dir vor, du hast zwei Freundesgruppen:
- Deine Freunde aus dem Spanischkurs. Menge A = {Julian, Tabea, Anna}
- Deine Freunde aus dem Musikverein. Menge B = {Anna, Franziska, Timo}
Mit der Vereinigungsmenge A ∪ B beantwortest du die Frage: Wer sind alle deine Freunde?
Die Antwort ist also A ∪ B = {Julian, Tabea, Anna, Franziska, Timo}
Achtung: Obwohl du Anna aus dem Spanischkurs und aus dem Musikverein kennst, nennst du sie in der Menge nur ein Mal. Schließlich ist sie nur ein Mensch!
Die Vereinigungsmenge A∪ B ist die Menge aller Elemente, die sich in der Menge A, in der Menge B oder in beiden Mengen befinden. Formal schreibst du sie so auf:
A∪ B = {x| x ∈ A v x ∈ B}
![Rendered by QuickLaTeX.com \[ \underbrace{A \cup B}_{\text{A vereinigt mit B}} \underbrace{=}_{\text{ist}} \underbrace{\{}_{\text{die Menge}} \underbrace{~~~~~x~~~~~}_{\text{aller x}} \underbrace{|}_{\text{für die gilt:}} \underbrace{x \in A}_{\text{x ist Element von A}} \underbrace{\vee}_{\text{und/oder}} \underbrace{x \in B}_{\text{x ist Element von B}} \}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-41ff157f1a05fc6d6ae1f2440bcdc8b7_l3.png)
Aber wie kannst du eine Vereinigungsmenge berechnen? Im Folgenden bekommst du eine Schritt-für-Schritt-Anleitung!
Vereinigungsmenge berechnen
Du kannst die Vereinigungsmenge in 2 Schritten einfach berechnen:
- Schreibe alle Elemente der Menge A und der Menge B zusammen in eine neue Menge.
- Streiche die Dopplungen raus.
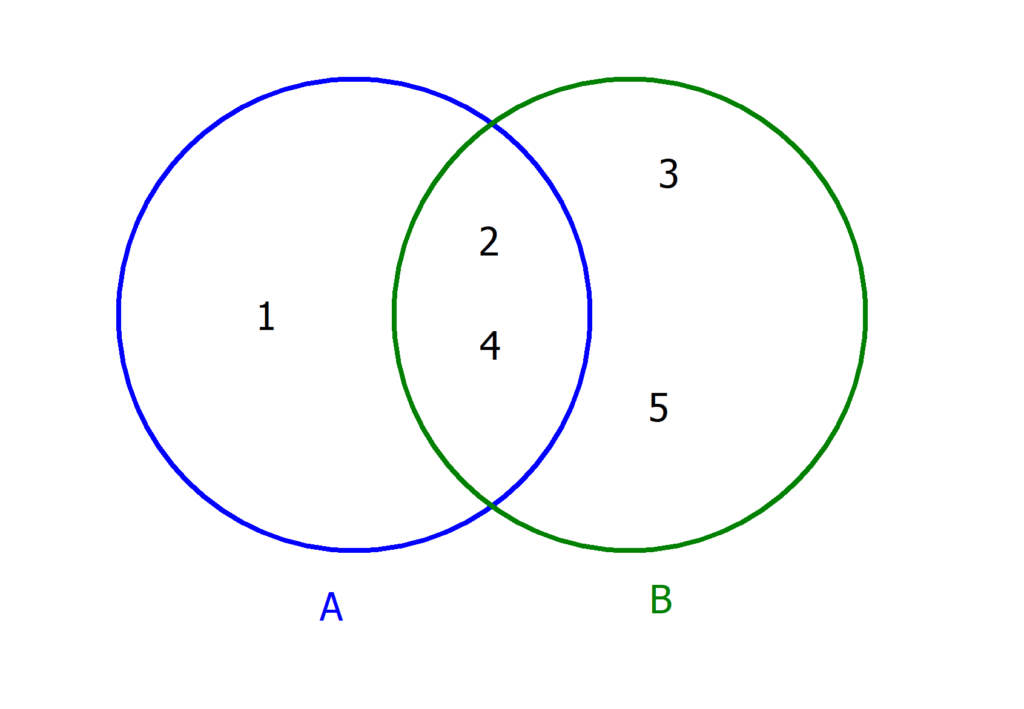
Beispiel 1: Bestimme die Vereinigungsmenge von A = {1, 2, 4} und B = {2, 3, 4, 5}.
- Schreibe alle Elemente hintereinander in eine neue Menge.
A ∪ B = {1, 2, 4, 2, 3, 4, 5} - Streiche die Dopplungen raus. Hier sind die Zahlen 2 und 4 doppelt.
A ∪ B = {1, 2, 4,2, 3,4, 5}
Übrig bleibt also A ∪ B = {1, 2, 4, 3, 5}.
Beispiel 2: Bestimme die Vereinigungsmenge von A = {1, 2, 3} und B = {1, 2, 3, 4, 5}.
Wie du auf dem Bild sehen kannst, ist A eine Teilmenge von B. Das bedeutet, dass alle Elemente von A auch in B sind. Auch hier gehst du gleich vor:
- Schreibe alle Elemente in einer neuen Menge zusammen.
A ∪ B = {1, 2, 3, 1, 2, 3, 4, 5} -
Streiche alle Dopplungen. Hier hast du die Zahlen 1, 2, und 3 jeweils doppelt.
A ∪ B = {1, 2, 3,1,2,3, 4, 5}
Du erhältst also A ∪ B = {1, 2, 3, 4, 5}.
Beispiel 3: Bestimme die Vereinigung der Mengen A = {1, 2, 3, 4, 5} und B = {1, 2, 3, 4, 5}.
Wie du sehen kannst, sind die Mengen A und B hier gleich.
- Schreibe alle Elemente hintereinander.
A ∪ B = {1, 2, 3, 4, 5, 1, 2, 3, 4, 5} -
Streiche alle Dopplungen. Hier sind die Zahlen 1, 2, 3, 4 und 5 doppelt.
A ∪ B = {1, 2, 3, 4, 5,1,2,3,4,5}
Daraus ergibt sich A ∪ B = {1, 2, 3, 4, 5}.
Beispiel 4: Berechne die Vereinigung der Mengen A = {1, 2} und B = {3, 4, 5}.
Auf dem Bild siehst du, dass A und B sich nicht überschneiden. Das nennst du auch disjunkt.
- Schreibe alle Elemente hintereinander in eine neue Menge.
A ∪ B = {1, 2, 3, 4, 5} - Streiche die Dopplungen raus. Hier hast du aber gar keine!
Du erhältst also direkt A ∪ B = {1, 2, 3, 4, 5}.
Beispiel 5: Berechne die Vereinigungsmenge von A = {1, 2, 3, 4, 5} und B = {}.
In diesem Beispiel hat B keine Elemente. Deshalb nennst du sie auch leere Menge.
- Schreibe alle Elemente hintereinander.
A ∪ B = {1, 2, 3, 4, 5} - Hier hast du wieder keine Dopplungen. Deshalb bist du schon fertig!
Du bekommst also direkt A ∪ B = {1, 2, 3, 4, 5}.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Vereinigungsmenge berechnen Regeln
Auch bei der Vereinigung gibt es in Mathe ein paar Rechenregeln.
Die Vereinigungsmenge ist nämlich…
- …kommutativ. Das bedeutet, dass A ∪ B = B ∪ A
-
…assoziativ. Das heißt, bei 3 Mengen gilt: A ∪ ( B ∪ C) = (A ∪ B) ∪ C
Vereinigungsmenge und Schnittmenge
Super, jetzt kennst du dich mit der Vereinigung von Mengen bestens aus! Es gibt aber noch viel mehr Mengenoperationen!
Die Schnittmenge A ∩ B ist das „Gegenstück“ zur Vereinigungsmenge A ∪ B.
- Die Vereinigungsmenge (∪) enthält alle Elemente aus der Menge A und der Menge B.
- Die Schnittmenge (∩) enthält nur die Elemente, die in beiden Mengen sind.
Beispiel: Bestimme die Vereinigungsmenge und Schnittmenge von A = {1, 2, 3} und B = {3, 4, 5}.
- Die Vereinigungsmenge A ∪ B = {1, 2, 3, 4, 5}
- Die Schnittmenge A ∩ B = {3}
Vereinigungsmenge — häufigste Fragen
(ausklappen)
Vereinigungsmenge — häufigste Fragen
(ausklappen)-
Was bedeutet A ∪ B bei zwei Mengen?A ∪ B bedeutet die Vereinigungsmenge von A und B, also alle Elemente aus A, aus B oder aus beiden. Du sammelst damit alles, was in mindestens einer der beiden Mengen vorkommt. Beispiel: {Julian, Tabea, Anna} ∪ {Anna, Franziska, Timo} = {Julian, Tabea, Anna, Franziska, Timo}.
-
Wie berechne ich die Vereinigungsmenge Schritt für Schritt?Du berechnest A ∪ B in zwei Schritten: Erst schreibst du alle Elemente aus A und B in eine neue Menge, danach streichst du alle Dopplungen. Beispiel: {1, 2, 4} ∪ {2, 3, 4, 5} → erst {1, 2, 4, 2, 3, 4, 5}, dann {1, 2, 4, 3, 5}.
-
Warum darf ein Element in der Vereinigungsmenge nur einmal stehen?Ein Element darf in der Vereinigungsmenge nur einmal stehen, weil eine Menge jedes Element nur einmal enthält. Doppelte Einträge würden keine neue Information hinzufügen, es bleibt ja dasselbe Element. Beispiel: Anna ist in A und in B, trotzdem schreibst du in A ∪ B Anna nur einmal.
-
Was passiert mit A ∪ B, wenn A eine Teilmenge von B ist?Wenn A eine Teilmenge von B ist, dann ist A ∪ B genau B. Das liegt daran, dass alle Elemente aus A schon in B enthalten sind und durch die Vereinigung nichts Neues dazukommt. Beispiel: A = {1, 2, 3}, B = {1, 2, 3, 4, 5} ergibt A ∪ B = {1, 2, 3, 4, 5}.
-
Was ist der Unterschied zwischen Vereinigungsmenge und Schnittmenge?Die Vereinigungsmenge A ∪ B enthält alle Elemente aus A und aus B, die Schnittmenge A ∩ B enthält nur die Elemente, die in beiden Mengen liegen. So siehst du, ob du „alles zusammen“ oder nur die „Überschneidung“ suchst. Beispiel: A = {1, 2, 3}, B = {3, 4, 5} führt zu A ∪ B = {1, 2, 3, 4, 5} und A ∩ B = {3}.
Venn Diagramm
Oftmals hilft es dir, die Mengen graphisch darzustellen, um die Vereinigungsmenge zu berechnen. Diese Grafik nennst du auch Venn Diagramm. Du möchtest mithilfe der Venn Diagramme noch weitere Mengenoperationen berechnen? Dann schau dir direkt unser Video dazu an!