Mathematische Symbole

Mathematische Symbole — Logik

Mathematisches Zeichen	Bedeutung	Beispiel	Latexcode
¬	„nicht“ (Negation)	¬ (9 ist gerade)	\lnot
∧	„und“(Konjunktion)	(12 ist gerade) ∧ 12 (ist durch 3 teilbar)	\land
∨	„oder“(Disjunktion)	A ∨ B	\lor
⇒	„daraus folgt“ (Implikation)	n ist durch 4 teilbar ⇒ n ist durch 2 teilbar	\Rightarrow
	„daraus folgt nicht“	n ist durch 2 teilbar n ist durch 4 teilbar	\nRightarrow
⇔	„genau dann wenn“ (Äquivalenz)	n ist durch 6 teilbar ⇔ n ist durch 2 und durch 3 teilbar	\Leftrightarrow
	„nicht genau dann wenn“	n ist eine Primzahl n ist ungerade	\nLeftrightarrow
∀	„für alle“ (Allquantor)	: 0 · n = 0	\forall
∃	„es existiert“ (Existenzquantor)	: 0 < n < 1	\exists
∃!	„es existiert genau ein“	: 2 · n = 6	\exists!
	„es existiert kein“	: n · 0 = 7	\nexists

Mathematische Symbole — Mengenlehre

Mathematisches Zeichen		Bedeutung	Beispiel	Latexcode
{…}		Mengenklammern	{1,2,3} ist die Menge, die die Elemente 1, 2 und 3 enthält	\{…\}
:=		„ist definiert als“	M := {1,2,3}	\coloneqq
∈		„ist Element von“	3 ∈ {7,3,2}	\in
∉		„ist kein Element von“	-3 ∉ N	\notin
⊆		„ist eine Teilmenge von“	Ø ⊆M für jede Menge M	\subseteq
		„ist keine Teilmenge von“	{1,2,4,5} {1,2,3,4}	\nsubseteq
⊇		„ist eine Obermenge von“	Z ⊇ N	\supseteq
		„ist keine Obermenge von“	N Z	\nsupseteq
∪		Vereinigung	{1,2} ∪ {7,3,2} = {1,2,3,7}	\cup
(oder: )		disjunkte Vereinigung	{1,2} {7,3,4} = {1,2,3,4,7}	\sqcup (oder: \dot\cup)
∩		Schnitt	{1,2} ∩ {7,3,2} = {2}	\cap
\		Komplement-/Differenzmenge	{7,3,2} \ {1,2} ={7,3}	\setminus
Δ		symmetrische Differenz	A Δ B := (A ∪ B) \ (A ∩ B)	\triangle
N		Menge der natürlichen Zahlen	N := {1,2,3,…} (manchmal auch {0,1,2,…})	\mathbb{N}
Z		Menge der ganzen Zahlen	Z := N ∪ {-n | n ∈ N}	\mathbb{Z}
Q		Menge der rationalen Zahlen	Q :={p/q | p ∈ Z, q ∈ Z\{0}}	\mathbb{Q}
I		Menge der irrationalen Zahlen	π, e, √2 ∈ I	\mathbb{I}
R		Menge der reellen Zahlen	R = Q ∪ I	\mathbb{R}
C		Menge der komplexen Zahlen	2i + 3 ∈ C	\mathbb{C}
{…  | …}		„für die gilt“	{a ∈ Z | a ist durch 2 teilbar} beschreibt die Menge der geraden Zahlen	\mid
Ø (oder: { })		leere Menge	{i, π, √2 } ∩ Q = Ø	\emptyset (oder: \{ \})
x		kartesisches Produkt	A x B := {(a,b) | a ∈ A, b ∈ B}	\times
P(…)		Potenzmenge	P({1,2}) = {Ø, {1}, {2}, {1,2}}	\mathcal{P}(…)

Mathematische Symbole — Rechnen und Vergleichen

Mathematisches Zeichen	Bedeutung	Beispiel	Latexcode
·	Malpunkt	32 = 3 · 3	\cdot
p/q	Bruch	½ = 0,5	\frac{p}{q}
!	Fakultät	3! = 3 · 2 · 1	!
Σ	Summenzeichen	(Gaußsche Summenformel)	\sum
Π	Produktzeichen	2 = 2n	\prod
≠	ungleich	7 ≠ 3 · 4	\neq
≈	ungefähr gleich	π ≈ 3,1416	\equiv
(…)2	hoch 2/zum Quadrat	4 = 22	(…)^2
√	(Quadrat-)Wurzel	2 = √4	\sqrt
	konjugiert komplexe Zahl		\overline{…}
<	kleiner als	1 < 2	<
>	größer als	x + 1 > x für jede reelle Zahl x	>
≤	kleiner gleich	n ≤ n2 für jede ganze Zahl n	\leq
≥	größer gleich	x2 ≥ 0 für jede reelle Zahl x	\geq
≡	äquivalent/kongruent/identisch	3 ≡ 1 mod 2	\equiv
∼	Zeichen für Äquivalenzrelation	a ∼ b	\sim
≅	isomorph	Existiert ein Isomorphismus f: G → H, dann G ≅ H	\cong
|	Teilbarkeitszeichen	4 | 8	\mid
|…|	Betrag einer Zahl	|-2| =2	\vert
∞	unendlich	tan(90°) → ∞	\infty

Mathematische Symbole — Funktionen

Mathematisches Zeichen	Bedeutung	Beispiel	Latexcode
f(x), g(x)	Schreibweise für Funktionen	f(x) = -x2, g(x) = 3x+2	f(x), g(x)
ο	Verkettung von Funktionen	(f ο g)(x) = -(3x+2)2	\circ
f'(x)	die erste Ableitung von f	f'(x) = -2x	f ^{\prime} (x)
df/dx	Ableitung von f nach x	df/dx = -2x	\frac{\mathrm{d}f}{\mathrm{d}x}
f“(x)	die zweite Ableitung	f“(x) = -2	f^{\prime\prime}(x)
→	Abbildungspfeil	f: R → R	\rightarrow
	Zuordnungspfeil	f : x -x2	\mapsto
f-1	Umkehrfunktion	f-1(x) = ½x ist Umkehrfunktion von f(x) = 2x	f^{-1}
(a,b)	offenes Intervall	f: (0,1) → R	(a,b)
[a,b]	abgeschlossenes Intervall	g: [-1,1] → [0,1]	[a,b]
→	Konvergenz pfeil	für x → ∞ gilt f(x) → – ∞	\rightarrow
∫… dx	unbestimmtes Integral	∫ 2x dx = x2	\int
	bestimmtes Integra l in den Grenzen a und b		\int\limits_{…}^{…}
e	Eulersche Zahl	e ≈ 2,7183	\mathrm{e}
p(A|B)	bedingte Wahrscheinlichkeit	p(A|B) = p(A∩ B)/p(B)	\mathrm{p}(A \mid B)

Mathematische Symbole — Geometrie und Vektoren

Mathematisches Zeichen	Bedeutung	Beispiel	Latexcode
⊥	orthogonal	g ⊥ h	\perp
||	parallel	(g ⊥ h ∧ j ⊥ h) ⇒ g || j	\parallel
	Vektor v		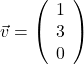\vec{v}
	2×2-Matrix	det = ad-bc	\left( \begin{array} {cc}{a & b \\ c & d} \end{array} \right)
< … , … >	Skalarprodukt		\langle … , … \rangle
||…||	Vektornorm		\Vert … \Vert
⊕	Vektor addition / direkte Summe		\oplus

Mathematische Symbole — Griechische Buchstaben

Mathematisches Zeichen	Bedeutung	Beispiel	Latexcode
α	alpha	oft als Winkel verwendet α=90°	\alpha
β	beta	tan (β)=sin (β)/cos (β)	\beta
γ	gamma	Für die Innenwinkel eines Dreiecks gilt: α + β + γ =180°	\gamma
δ	delta	wird bei der partiellen Ableitung verwendet:	\delta
ε	epsilon	In der Konvergenzanalyse : Sei ε > 0 …	\varepsilon
λ	lambda	oft als Parameter f(x) = λx	\lambda
μ	mü	bezeichnet den Erwartungswert in einer Normalverteilung z.B. μ = 0	\mü
σ	sigma	kommt vor als Standardabweichung , σ2 ist die Varianz	\sigma
π	Kreiszahl pi	Kreisfläche A = 2πr2	\pi
φ	phi	auch oft ein Winkel φ = 2π	\varphi
ω	omega	(Winkelgeschwindigkeit in der Physik)	\omega

Mengenlehre

So eine Liste mathematischer Symbole ist schon sehr praktisch. Da kann man mal schnell die Bedeutung von bestimmten Mathe Zeichen nachschauen — wie die des orthogonal Zeichens oder von Symbolen der Mengenlehre. Wenn du genauer wissen willst, was es mit diesen ganzen Symbolen der Mengenlehre auf sich hat, dann schau doch bei unserem Video  dazu vorbei!