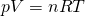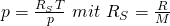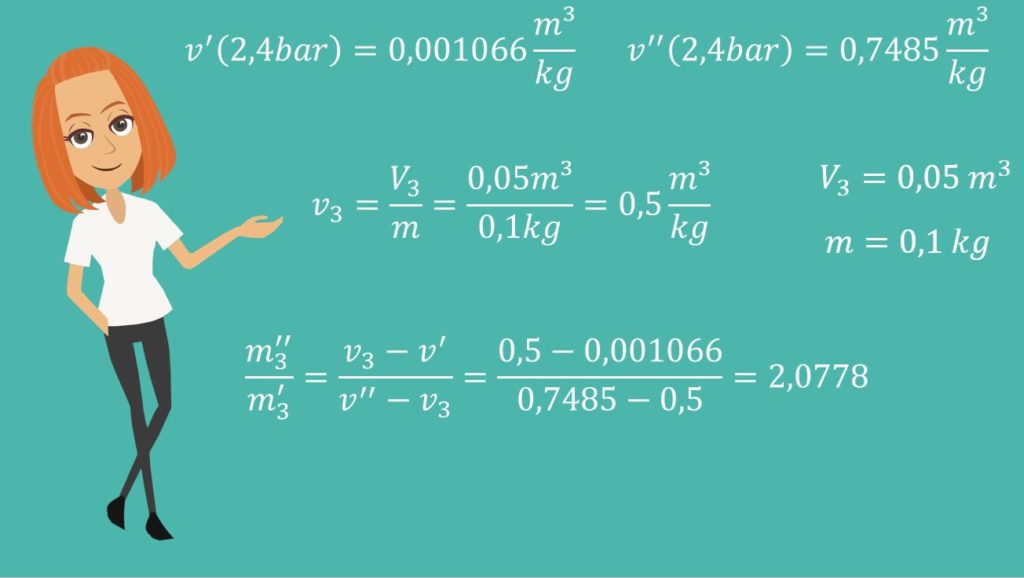Nassdampfgebiet
Du hast sicher schon mal Wasser in einem Topf mit geschlossenem Deckel zum Kochen gebracht und dich gefragt, welche thermodynamischen Vorgänge währenddessen passieren. Dass das Nassdampfgebiet dabei eine entscheidende Rolle spielt, können wir vorab schon verraten und auch den Nassdampf und die Taulinie bekommst du in diesem Beitrag erklärt.
Inhaltsübersicht
Was sind der Nassdampf und das Nassdampfgebiet?
Das Nassdampfgebiet besteht aus gasförmigen und flüssigen Phasen. Es stellt also den sichtbaren Wasserdampf am Deckel dar. Nassdampf ist damit eine Mischung aus Dampf und Flüssigkeit desselben Stoffes, bei dem beide Zustände ihre Sättigungstemperatur erreicht haben. Schauen wir uns das Nassdampfgebiet in Form eines Graphens an:
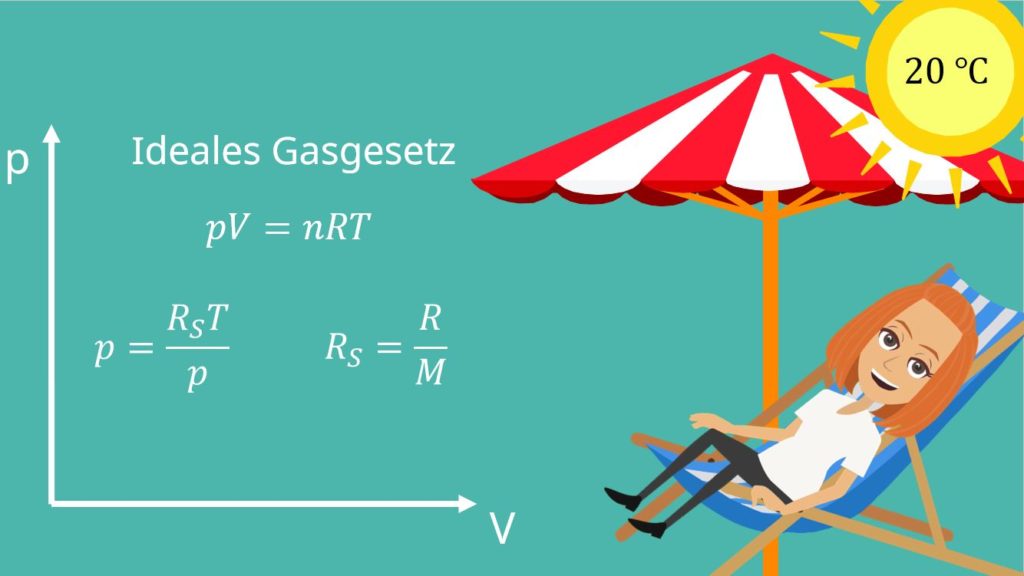
In der Regel verwenden wir für die Veranschaulichung des Nassdampfgebiets ein Diagramm, das auf der x-Achse das spezifische Volumen V und auf der y-Achse den Druck p stehen hat. Zunächst wollen wir eine isotherme Linie betrachten. Das heißt, wir haben immer die gleiche Temperatur von zum Beispiel 20 Grad. Um dies durchführen zu können, brauchen wir also eine Formel, die p in Abhängigkeit von V darstellt. Dabei kann uns das ideale Gasgesetz helfen.
Grenzen des Nassdampfgebiets
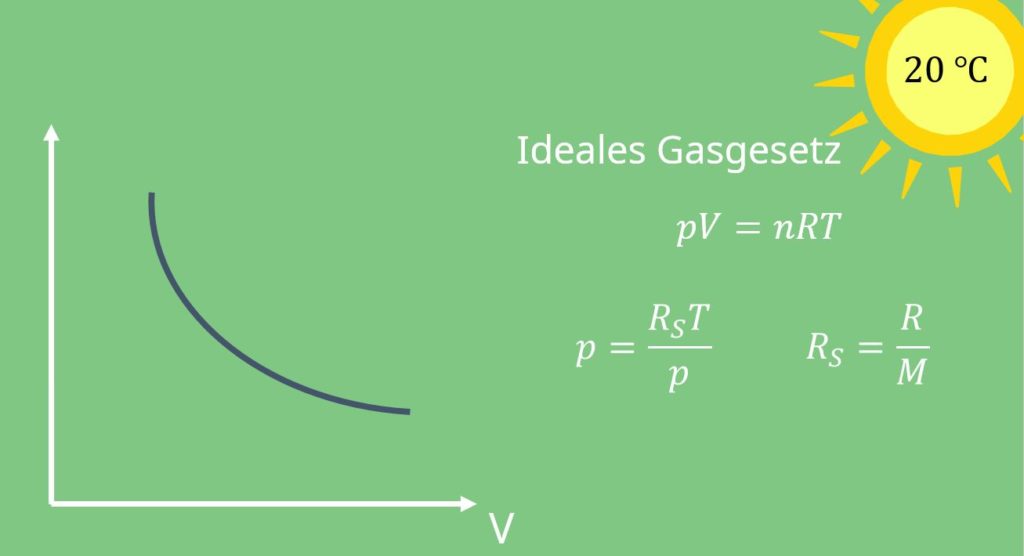
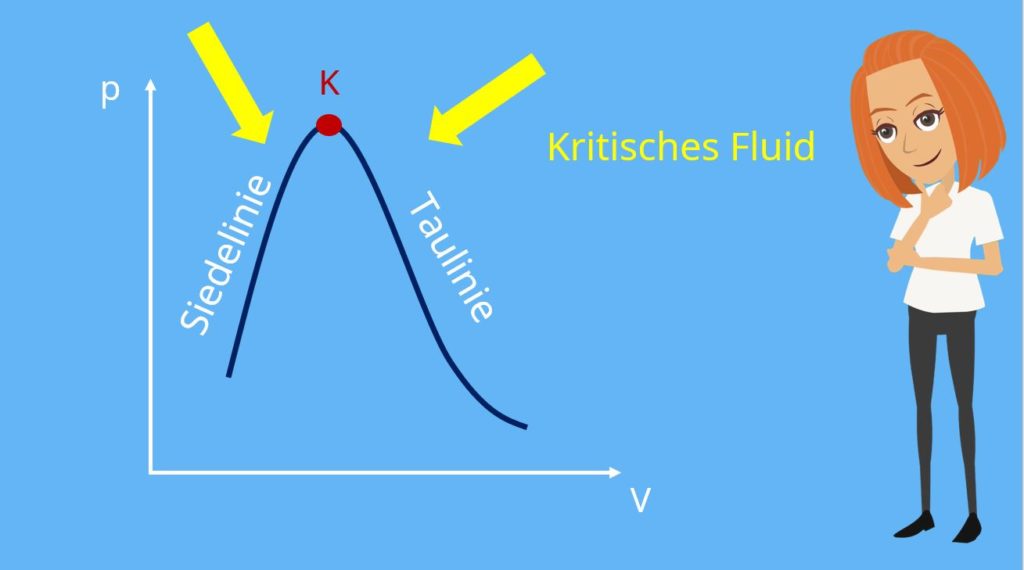
Damit erhalten wir eine Hyperbel. In der Realität sieht das aber leider anders aus. Wenn wir das spezifische Volumen immer weiter verringern, und damit die Dichte erhöhen, erhalten wir irgendwann Flüssigkeit. Wenn wir in diesen Bereich kommen, nennen wir das Nassdampfgebiet, da hier der Nassdampf vorherrscht. Dieser Bereich sieht etwa wie eine umgedrehte Parabel aus. Der rechte Arm ist die sogenannte Taulinie, also der Punkt, bei der der erste Tropfen Wasser entsteht. Der linke Arm ist die sogenannte Siedelinie. Hier bildet sich die erste Dampfblase, wenn wir die Dichte etwas reduzieren. Ruf dir hier für das Verständnis noch einmal die oben genannte Definition von Nassdampf ins Gedächtnis. Der Schnittpunkt ist der kritische Punkt. Alles darüber wird „kritisches Fluid“ genannt und zeichnet sich dadurch aus, dass man flüssig und gasförmig nicht mehr unterscheiden kann.
Taulinie, Siedelinie und Gesetz der abgewandten Hebelarme
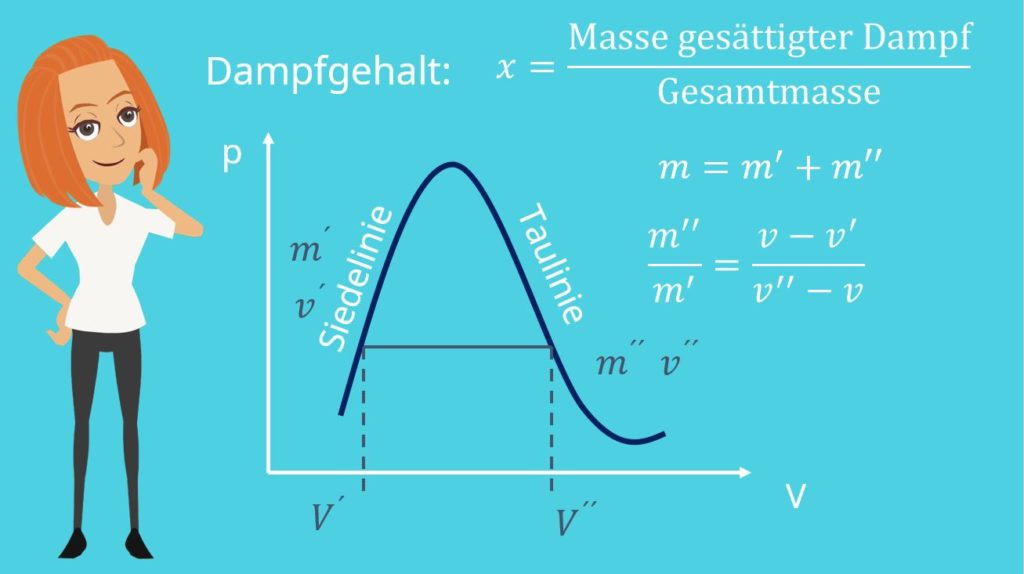
Wir kennen jetzt die Grenzen des Nassdampfgebiets, doch uns interessiert natürlich, was im Inneren, also mit dem Nassdampf, passiert. Wie du dir sicher denken kannst, haben wir unser Fluid sowohl flüssig, als auch gasförmig vorliegen. Das müssen wir aber irgendwie quantifizieren können, was wir mit Hilfe des Dampfgehaltes machen:
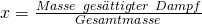
Die Masse des gesättigten Dampfes ist genau die, die wir haben, wenn wir auf der Taulinie wären. Die Zustandsgrößen an diesem Punkt versehen wir jetzt mit zwei Strichen:
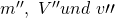
Analog dazu haben wir natürlich die Masse, die noch nicht verdampft ist und dann auf der Siedelinie liegt. Diese versehen wir mit einem Strich:
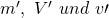
Die Gesamtmasse ergibt sich aus der Summe der beiden Massen:
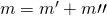
Damit können wir dann das Gesetz der abgewandten Hebelarme verwenden. Dieses ist definiert als:
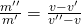
Als kleiner Überblick noch einmal:
- Die Masse des gesättigten Dampfes ist die auf der Taulinie
- Die Masse, die noch nicht verdampft ist, befindet sich auf der Siedelinie
Nassdampf erzeugen
Das alles mit Nassdampf, Taulinie und Siedelinie klingt noch etwas kompliziert. Schauen wir uns deshalb ein Beispiel an: Wir betrachten einen Kolben mit flüssigem Wasser der Masse m von 0,1 Kilogramm bei 30 Grad. Diesen führen wir bei konstantem Druck von 2,4 bar Wärme zu. Das heißt wir erhitzen ihn. Bei der Temperatur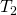 
tritt gerade die erste Dampfblase auf. Hier hören wir aber nicht auf, sondern erhitzen weiter bis zu einem Volumen 
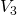von 0,05 Kubikmeter. Hier wird der Kolben festgehalten und wir erwärmen weiter bis zur Temperatur 
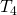. Hier ist dann das Wasser komplett verdampft.
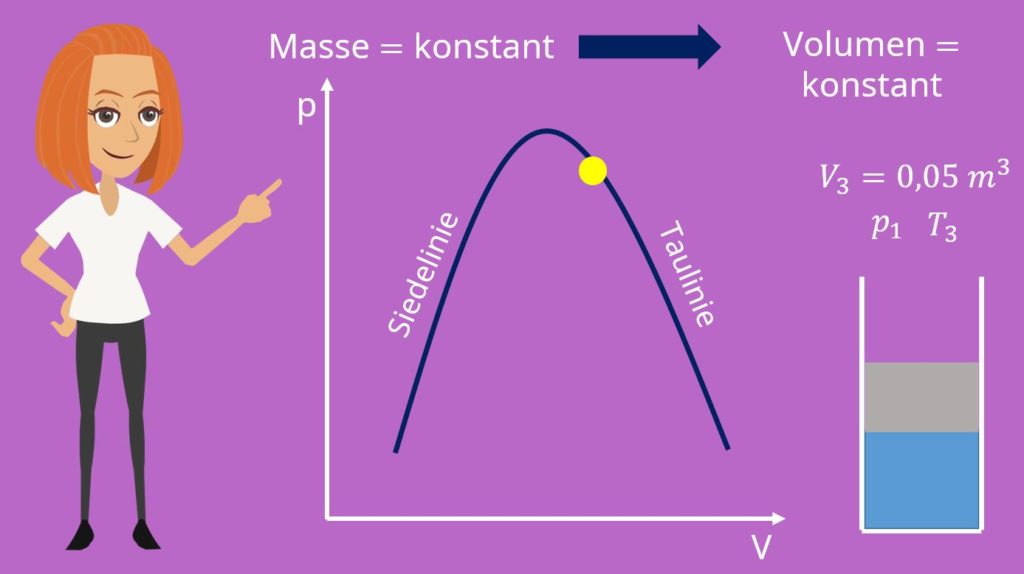
Weiter für die Rechnung im Nassdampfgebiet wollen wir jetzt den Dampfgehalt bei 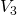bestimmen. Dafür zeichnen wir uns erstmal qualitativ auf, wie wir denn das Nassdampfgebiet durchschreiten. Wir können vier Punkte ausmachen: Der erste Punkt liegt im flüssigen, also links der Siedelinie. Dann gehen wir isobar, also bei konstantem Druck Richtung Nassdampfgebiet. Deshalb gehen wir parallel zur x-Achse entlang. Punkt zwei liegt genau auf der Siedelinie, da hier die erste Dampfblase erscheint. Punkt drei liegt irgendwo im Nassdampfgebiet. Allerdings wissen wir, dass wir weiter isobar geblieben sind und deshalb weiterhin parallel zur x-Achse das Nassdampfgebiet durchlaufen. Beim Punkt vier halten wir das Volumen konstant. Da die Masse auch konstant ist, wird das spezifische Volumen ebenso konstant bleiben und der Druck muss sich erhöhen. Im Diagramm gehen wir dann also senkrecht nach oben bis zur Taulinie. Denn hier an der Taulinie angekommen, sind wir ja gerade vollständig verdampft.
Beispielrechnung im Nassdampfgebiet
Wir wissen jetzt, was der Nassdampf ist, wie wir das Nassdampfgebiet durchlaufen und was an der Taulinie passiert. Für den Dampfgehalt, brauchen wir die Masse an Dampf. Dafür können wir das Gesetz der abgewandten Hebelarme verwenden. Wir brauchen nur: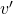 
und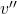 
.
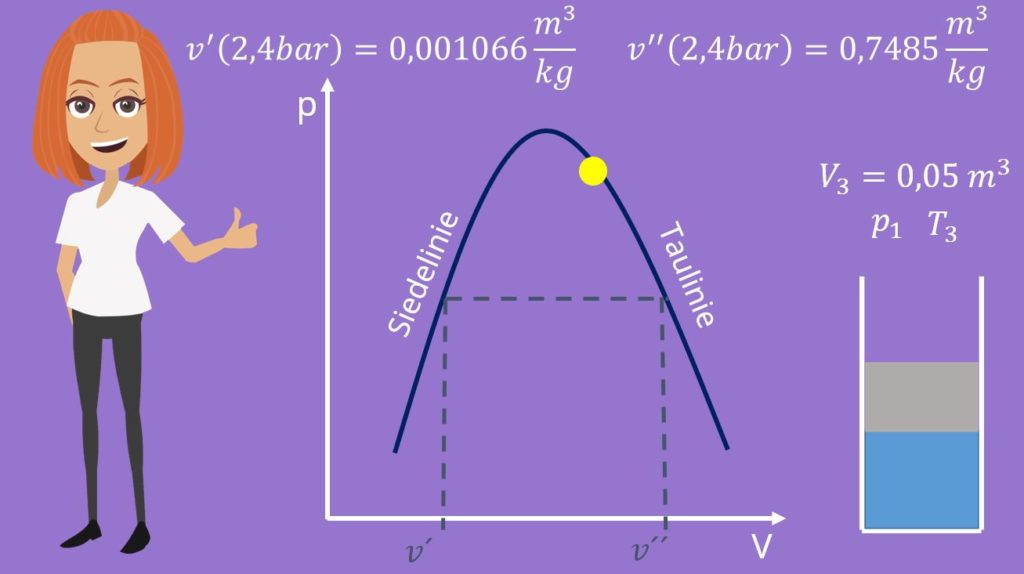
Diese finden wir für den spezifischen Druck in Tabellen mit:
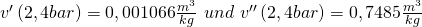
Jetzt brauchen wir nur noch das spezifische Volumen. Wir können es ganz einfach bestimmen mit:
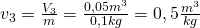
Damit können wir uns jetzt, mit Hilfe des Gesetztes der abgewandten Hebelarme, das Verhältnis von Flüssigkeit und Dampf bestimmen:
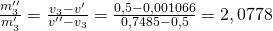
Wir haben also noch etwa doppelt so viel Dampf wie Flüssigkeit übrig. Um jetzt auf den Dampfgehalt zu kommen, müssen wir das ein wenig umformen. Zunächst betrachten wir den Kehrwert:
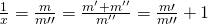
Das Verhältnis von Dampf zu Flüssigkeit kennen wir ja bereits und erhalten:
Bilden wir davon jetzt den Kehrwert, erhalten wir die gesuchte Größe:
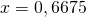
Das heißt 66,75 Prozent des Wassers an dem Punkt, an dem wir den Kolben festhalten, sind gasförmig.
Nun weißt du, was Nassdampf ist und wie du ein Nassdampfgebiet abgrenzen kannst genauso wie dir auch der Begriff Taulinie kein Fremdwort mehr sein sollte.