Skalenerträge
Konstante, steigende und abnehmende Skalenerträge werden innerhalb der VWL und Mikroökonomie der Produktionstheorie zugeordnet. Wir erklären dir anhand von Beispielen was sich dahinter versteckt, schauen uns die formale Schreibweise an und zeigen dir wie man Skalenerträge berechnet.
Zu viel Text? In unserem Video zum Skalenerträge erklären wir dir alles wichtige rund um das Thema kurz, prägnant und super easy verständlich.
Inhaltsübersicht
Skalenerträge Definition
Als Skalenerträge bezeichnet man die Veränderung des Outputs bei proportionaler Änderung der Inputfaktoren. Je nachdem ob der Output proportional, überproportional oder unterproportional wächst spricht man von konstanten, steigenden oder abnehmenden Skalenerträgen.
Die Begriffe Skalenertrag (engl. returns to scale) und Skaleneffekt werden in der Betriebswirtschaftslehre und in der Mikroökonomie als ein Bestandteil der Produktionstheorie definiert. Skalenerträge, auch als Niveaugrenzprodukt bezeichnet, geben die Rate an, um die sich der Output bei Erhöhung der Produktionsfaktoren verändert.
Damit sind sie eine Eigenschaft der Produktionsfunktion.
Skaleneffekte dagegen sind genau jene Effekte, die durch steigende oder fallende Skalenerträge entstehen.
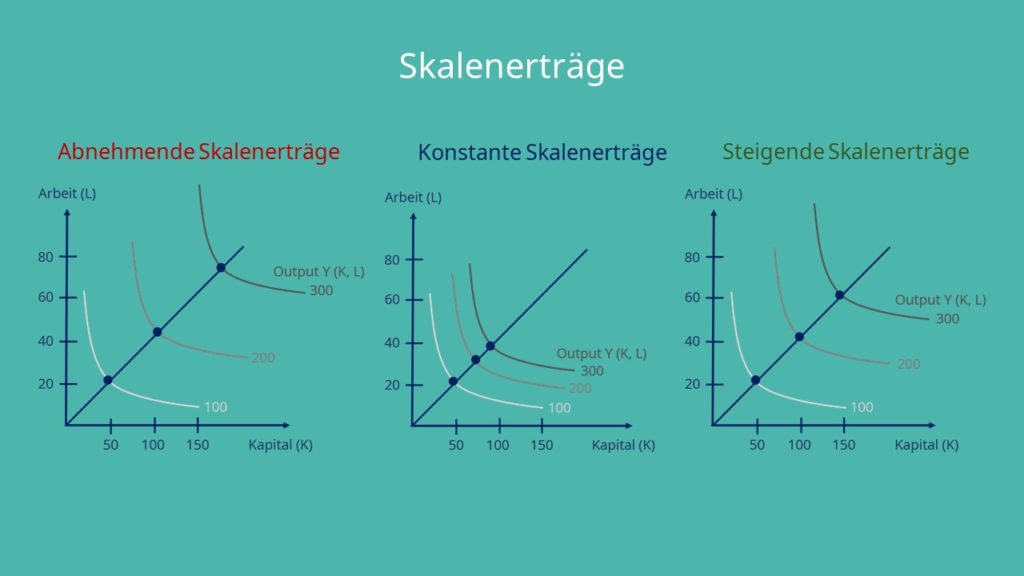
Konstante, zunehmende und abnehmende Skalenerträge
Drei Möglichkeiten können bei einer Produktion vorliegen: Entweder handelt es sich um konstante Skalenerträge, zunehmende Skalenerträge oder um abnehmende Skalenerträge.
Betrachtet man die Kostenstruktur, lassen sich Skalenerträge folgendermaßen erklären:
- Konstante Skalenerträge: Die Durchschnittskosten bleiben bei zunehmender Produktionsmenge konstant.
- Steigende Skalenerträge: Die Durchschnittskosten sinken bei zunehmender Produktionsmenge.
- Fallende Skalenerträge: Die Durchschnittskosten steigen bei zunehmender Produktionsmenge.
Formal schreibt man:
-
konstante Skalenerträge:

-
steigende Skalenerträge:

-
fallende Skalenerträge:

Die linke Seite stellt jeweils den Input und dessen Erhöhung, die rechte Seite den Output und dessen Erhöhung dar. Bei einer Produktion können auch alle drei Fälle vorliegen. Ein möglicher Verlauf wäre etwa, dass bei geringem Output durch eine Spezialisierung zuerst steigende Skalenerträge zu erkennen sind. Es folgen konstante Skalenerträge und bei hohem Output beispielsweise durch Kommunikations- und Organisationsprobleme abnehmende Skalenerträge.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Konstante Skalenerträge
Es handelt sich um konstante Skalenerträge (constant returns of scale), wenn der Output sich um den gleichen Faktor a erhöht wie der Input – Wenn also bei Veränderung der Inputfaktoren um den Faktor a auch die Produktionsmenge um den Faktor a ansteigt. Wird beispielsweise der Input um 200 Einheiten erhöht, steigt auch der Output proportional um genau diese 200 Einheiten an. Es gilt:

Konstante Skalenerträge liegen also vor, wenn bei einer Erhöhung der Inputfaktoren die Produktionsmenge proportional ansteigt, z.B.: Produktionsfaktoren steigen um +25% und die Produktionsmenge steigt ebenfalls um +25%.
Beispielsweise bei Dienstleistungen und im Handwerk handelt es sich meist um konstante Skalenerträge, da sich die Inputfaktoren nicht beziehungsweise kaum verändern lassen. Für konstante Skalenerträge ist die Produktionsfunktion linear homogen vom Grad 1.
Konstante Skalenerträge: Beispiel
Ein Beispiel für einen konstanten Skalenertrag wäre etwa folgendes Szenario: Eine kleine Dorfbäckerei besitzt eine Teigknetmaschine. Diese ermöglicht die tägliche Produktion von 250 Brezen. Doch die Nachfrage nach Brezen ist in den vergangenen Monaten deutlich gestiegen. Daher wird eine weitere Knetmaschine beschafft. Der Inputfaktor wurde also verdoppelt. Die tägliche Produktionsmenge steigt in diesem Zuge auf 500 Brezen an. Auch der Output wurde somit verdoppelt und es handelt sich um konstante Skalenerträge.
Steigende Skalenerträge
Steigende Skalenerträge (Increasing returns to scale oder economies of scale) liegen vor, wenn die Produktionsmenge, der Output, um mehr als den Faktor a, um den der Input erhöht wird, ansteigt.
Wird also beispielsweise der Input um 200 Einheiten erhöht und der Output steigt um 201 Einheiten oder mehr, handelt es sich um zunehmende Skalenerträge. Formal schreibt man:

Economies of Scale liegen also vor, wenn bei einer Erhöhung der Inputfaktoren die Produktionsmenge überproportional ansteigt, z.B.: Produktionsfaktoren steigen um +25% und die Produktionsmenge steigt um +30%.
Zunehmende Skalenerträge können aus verschiedenen Gründen auftreten:
- Kosteneinsparung durch größere Produktionsmittel, z.B. kostet ein Ofen mit Kapazität von 400 Brezen weniger als zwei Öfen mit jeweiliger Kapazität von 200 Brezen
- Spezialisierungsvorteil bei einer höheren Produktionsmenge: Komplexe Arbeitsschritte können in viele kleine Unteraufgaben aufgeteilt werden. Die einfachen Teilschritte ermöglichen Lernkurveneffekte, Automatisierung und erhöhte Geschwindigkeit
- Vorteile bei entwicklungsintensive Produkten durch Massenproduktion: der kostenintensive Anteil an der Produktion, die Entwicklung, wurde bereits geleistet und kann nun auf eine höhere Produktionsmenge verteilt werden. Die Pro-Stück-Kosten sinken dadurch. Beispiele: Autoindustrie, Pharmaindustrie, Software
- Abnehmende Stückkosten bei steigender Produktion: Die Fixkosten bei der Beschaffung von Produktionsfaktoren können auf eine Produktionsmenge aufgeteilt werden. Somit nehmen die Stückkosten ab. Dahinter steht das Prinzip der Fixkostendegression .
- Bei aufeinanderfolgenden Fertigungsstufen können sich die Losgrößen besser aufeinander abstimmen Werden beispielsweise zur Produktion einer Torte eineinhalb Päckchen Backpulver benötigt, müssen trotzdem zwei Päckchen beschaffen werden. Es entsteht somit ein Rest eines halben Päckchens. Bei der Produktion von zwei Torten dagegen muss nicht die doppelte Menge an Backpulver beschaffen werden, sondern nur 3 Päckchen. Der Inputfaktor wird effektiver genutzt und die Losgrößenabstimmung verbessert.
Steigende Skalenerträge: Beispiel
In der kleinen Dorfbäckerei stellen die folgenden Situationen Beispiele für steigende Skalenerträge dar:
Bisher wurde der Grundteig für die Roggenbrötchen und das Roggenbaguette getrennt voneinander gemischt und geknetet. Die Zutaten für diesen Grundteig sind jedoch identisch. Daher entscheidet sich der Bäckermeister dazu diese Arbeitsschritte zusammenzulegen. Somit spart er sich Arbeitszeit, die Knetmaschine arbeitet nur einmal (Stromeinsparungen) und die Losgrößen lassen sich besser aufeinander abstimmen, da die Menge an Hefe, die er für beide Brotsorten benötigt exakt dem Pack maß der Hefe entspricht.
Economies of Scale: Beispiel
Bisher war für den Verkauf nur eine Mitarbeiterin zuständig. Doch zu den Stoßzeiten kommt es immer wieder zu einer langen Warteschlange. Der Bäckermeister entscheidet sich einen weiteren Mitarbeiter für den Verkauf einzustellen. Die beiden Verkäufer arbeiten gut zusammen, sind weniger gestresst und es entstehen keine langen Schlangen mehr vor der Bäckerei. Das begeistert die Kunden und lockt neue Kunden in die Bäckerei. Dadurch steigt der tägliche Verkauf von 100 Baguette auf 250 an. Der Output hat sich also bei einer Verdopplung des Inputs mehr als verdoppelt.
Abnehmende Skalenerträge
Für abnehmende Skalenerträge (decreasing returns to scale oder diseconomies of scale) gilt, dass die Produktionsmenge um weniger als den Faktor a, um den der Input erhöht wird, ansteigt. Wird also der Input um 200 Einheiten erhöht, der Output jedoch um maximal 199 Einheiten steigt.
Bei einer Zunahme aller Produktionsfaktoren steigt die Produktionsmenge somit nur unterproportional. Es gilt:

Abnehmende Skalenerträge liegen also vor, wenn bei einer Erhöhung der Inputfaktoren die Produktionsmenge unterproportional ansteigt, z.B.: Produktionsfaktoren steigen um +25% und die Produktionsmenge steigt um +20%.
Abnehmende Skalenerträge können folgende Ursachen haben:
- Schlechte Einarbeitung von neuen Mitarbeitern
- Verwaltungsprobleme bei Unternehmensexpansion
- Schlechtere Standortbedingungen bei neuem Standort im Vergleich zu bisherigen Standorten
- Schlechte interne Kommunikation und daraus resultierende doppelte Ausführung von Arbeitsschritten
Abnehmende Skalenerträge: Beispiel
Für unseren Bäckermeister läuft das Geschäft gut. Besonders die 150 Croissants, die eine Mitarbeiterin täglich produziert, kommen gut an und sind jeden Morgen schnell ausverkauft. Daher entscheidet er sich einen weiteren Mitarbeiter einzustellen. Dieser ist jedoch leider weniger motiviert und arbeitet deutlich langsamer als die erfahrene Mitarbeiterin. Er produziert so täglich nur 110 zusätzliche Croissants, nicht die erhofften 150. Der Output hat sich also bei einer Verdopplung des Inputs gerade einmal um knapp über 70 Prozent erhöht.
Skalenertrag berechnen: Beispiel
Ist die Summe der Exponenten der Produktionsfunktion gleich 1, sind die Skalenerträge konstant. Ist sie größer 1, sind sie steigend und ist sie kleiner 1, sind die Skalenerträge abnehmend.
Zur Berechnung von Skalenerträgen folgendes Beispiel:
In der Bäckerei wird mithilfe von drei Mitarbeitern (a), zwei Knetmaschinen (b) und einem Ofen (c) die tägliche Menge an Backwaren (Output) produziert. Die Produktionsfunktion lautet:

Mit der Eröffnung einer weiteren Filiale werden die eingesetzten Inputfaktoren verdoppelt.
Die neue Produktionsfunktion lautet also:




Der Output kann so durch eine  -fache Erhöhung des Inputs um das
-fache Erhöhung des Inputs um das  -fache gesteigert werden.
-fache gesteigert werden.
Auf unser Beispiel bezogen heißt das:

Setzt man nun a = 3, b= 2 und c = 1 für die Mitarbeiter, die Knetmaschinen und den Ofen ein und λ=2 erhält man:




56 ist größer als 28. Die Bäckerei produziert also mit steigenden Skalenerträgen.
Output vor der Erhöhung der Inputfaktoren: 
Output nach der Erhöhung der Inputfaktoren: 
Der Output vor der Erhöhung der Inputfaktoren beträgt 14. Nach der Erhöhung beträgt er nicht nur das Doppelte, sondern mit 56 sogar viermal so viel wie vor der Erhöhung.
Skalenerträge und Produktionsfunktion
Die Skalenelastizität gibt an, um wieviel Prozent sich, bei einer Erhöhung der Inputfaktoren (Produktionsfaktoren) um ein Prozent, der Output (Produktionsmenge) erhöht.
Bei einer Skalenelastizität mit dem Wert 1, spricht man von konstanten Skalenerträgen. Bei einigen Produktionsfunktionen hat die Skalenelastizität immer den gleichen Wert. Beispiele hierfür sind etwa die Leontief-Produktionsfunktion oder auch die Cobb-Douglas-Produktionsfunktion . Sie haben durchgehend eine Skalenelastizität von 1. Und bei jeder Vervielfachung des Inputs vervielfacht sich der Output um die gleiche Menge. Diese Produktionsfunktionen werden homogene Produktionsfunktionen genannt. Für konstante Skalenerträge ist die Produktionsfunktion linear homogen vom Grad 1. Homogenitätsgrad und Skalenelastizität stimmen also überein.
Bei einer Skalenelastizität von mehr als 1 spricht man von steigenden Skalenerträgen. Die Produktion steigt hier relativ gesehen stärker an als die eingesetzten Faktoren. Das heißt im Umkehrschluss, dass der Faktorverbrauch pro Stück wie auch die durchschnittlichen Kosten sinken.
Bei konstanten Skalenerträgen hat also die Produktionsfunktion einen Homogenitätsgrad von 1. Die Produktionsfunktion ist linear homogen. Ob eine Produktionsfunktion unter- oder überlinear homogen ist lässt sich im Isoquanten Diagramm folgendermaßen ermitteln: Zeichnet man einen Strahl durch den Ursprung, sind bei konstanten Skalenerträgen die Abstände zwischen den Isoquanten gleichbleibend.