Hydrostatischer Druck
Wenn du schon einmal Tauchen warst, dann bist du dem hydrostatischen Druck begegnet. Was der hydrostatische Druck ist und was er mit dem Tauchen zu tun hat, erfährst du hier.
Du kannst besser lernen, wenn du die entsprechende Thematik in einem Video sehen kannst? Keine Sorge, denn auch zum hydrostatischen Druck haben wir ein Video , das du dir gerne ansehen kannst.
Inhaltsübersicht
Hydrostatischer Druck einfach erklärt
Beginnen wir damit, was hydrostatischer Druck ist und welche wichtigen Formeln es in diesem Zusammenhang gibt.
Hydrostatischer Druck ist der Druck innerhalb eines ruhenden Fluids, der aufgrund der Gravitationswechselwirkung zwischen den Fluidteilchen und der Erde entsteht.
Hydrostatischer Druck hat zwei wesentliche Charakteristiken. Erstens besitzt er innerhalb eines Fluids in allen Richtungen denselben Betrag, und zweitens wirkt er immer senkrecht auf jede Fläche, die im Kontakt mit dem Fluid steht. Als eine Form des Drucks besitzt der hydrostatische Druck die Einheit bar oder Pascal (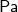
).
Wenn wir den Boden eines Behälters mit einem Fluid durch 
beschreiben und uns zwei Punkte 
und 
oberhalb des Bodens wählen, dann gilt für die Differenz im hydrostatischen Druck 
zwischen diesen zwei Punkten
.
Hier ist 
die Dichte des Fluids und 
die Schwerebeschleunigung.
Häufig wird als Referenz die Oberfläche des Fluids genommen, d.h. man betrachtet den hydrostatischen Druck in Abhängigkeit der Tiefe unterhalb der Fluidoberfläche. In diesem Fall ergibt sich für den Druck 
im Punkt
,
wobei 
die Tiefe unterhalb der Fluidoberfläche, also die Höhe der Wassersäule oberhalb des Punktes , beschreibt und 
der Umgebungsdruck ist, der auf der Oberfläche des Fluids wirkt. Befindet sich die Fluidoberfläche im Kontakt mit Luft, dann entspricht dieser Umgebungsdruck gerade dem Atmosphärendruck, welcher häufig durch einen Wert von 
approximiert wird.
Allgemeine Formel
Wir stellen uns einen Behälter mit Wasser vor. Innerhalb des Wassers betrachten wir ein kleines quaderförmiges Wasservolumen mit dem Volumen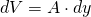 
, wobei 
die große Fläche des Volumenelementes ist. Dieses kleine Volumen wird in keine Richtung beschleunigt und befindet sich daher in einem Kräftegleichgewicht. Von Interesse ist das Kräftegleichgewicht in 
-Richtung.
Es wirken drei Kräfte auf das Volumenelement: Einerseits die Gravitationskraft, die mit 
gegeben ist und andererseits die Kräfte, die auf der oberen und unteren Fläche wirken, die durch
für die untere Fläche und
für die obere Fläche
gegeben sind. Wenn die Summe dieser drei Kräft gleich Null setzt, erhält man durch Umstellen
.
Hydrostatischer Druck nimmt also mit zunehmender Höhe ab, was zu erwarten war, da die Menge an Wasser oberhalb eine Punktes mit steigender Höhe abnimmt. Durch Lösen dieser Differentialgleichung unter der Annahme einer von der Höhe unabhängigen Dichte kann man die zu Beginn genannten Formeln erhalten. Eine detaillierte Rechnung hierzu kannst du in unserem Beitrag zum Druck in ruhenden Flüssigkeiten
finden. Ebenso kannst du in diesem Zusammenhang bei unserem Beitrag zur Auftriebskraft
vorbeischauen.
Pascal’sches Gesetz
Die Gleichung für den hydrostatischen Druck zeigt uns, dass sich bei Änderung des Umgebungsdruck der Druck innerhalb des Fluids unabhängig von der Höhe um den selben Betrag ändert. Diese Beobachtung wird als Pascal’sches Gesetz (oder auch Pascal’sches Prinzip) genannt und kann folgendermaßen präzisiert werden
Druck, der auf ein eingeschlossenes Fluid ausgeübt wird, verteilt sich unverändert auf jeden Teil des Fluids.
Eine sehr anschauliche Anwendung, die sich das Pascal’sche Gesetz zu Nutze macht, ist die hydraulische Hebebühne. Dabei erzeugt eine Kraft 
die auf die Fläche 
des kleinen Kolbens wirkt eine Änderung im hydrostatischen Druck, die auf die Fläche 
des großen Kolbens übertragen wird. Es resultiert dadurch eine Kraft 
auf den großen Kolben. Da nach dem Pascal’schen Gesetz der Druck gleichmäßig im gesamten Fluid verteilt wird, gilt
oder
und umgestellt auf
.
Da die Fläche des großen Kolbens viel größer als die Fläche des kleinen Kolbens ist, ist die auf den großen Kolben wirkende Kraft ebenfalls viel größer als . Dadurch kann eine kleine Kraft zu einer großen Kraft verstärkt werden. Somit braucht man beispielsweise keine allzu große Kraft, um ein PKW zu heben.
Hydrostatisches Paradoxon
Die Gleichung für den hydrostatischen Druck sagt aber auch aus, dass hydrostatischer Druck nur von der Höhe der Fluidsäule abhängt. Das heißt, für eine gegebene Höhe spielt die Form des Behälters keine Rolle. Eine sehr elegante Methode das zu beobachten, sind die sogenannten kommunizierenden Röhren. Dabei handelt es sich um verschieden geformte Röhren, die miteinander verbunden sind. Abhängig von der Form, würde man unterschiedliche Werte des hydrostatischen Drucks am Boden erwarten. Entsprechend der Gleichung müsste dann die Höhe des Fluidspiegels unterschiedlich sein. Tatsächlich beobachtet man aber, dass die Höhe in allen Röhren gleich ist. Diese Beobachtung bezeichnet man als hydrostatisches Paradoxon, dessen Aussage wie folgt lauten kann
Hydrostatischer Druck innerhalb eines Fluids hängt nur von der Fluidhöhe ab und nicht von der Form des Gefäßes, indem sich das Fluid befindet.
Berechnungsbeispiel
Als ein kleines Berechnungsbeispiel schauen wir uns eine Hebebühne an. Der große Kolbe habe einen Radius von 
, der kleine Kolben einen Radius von 
. Mit welcher Kraft musst du dann auf den kleinen Kolben drücken, damit der große Kolben einen Wagen der Masse 
heben kann?
Nach der Formel im Unterabschnitt zum Pascal’schen Gesetz gilt
.
Wir interessieren uns hier für die Kraft , die auf den kleinen Kolben ausgeübt werden muss. Umgestellt auf erhalten wir also
.
Die Kraft , die auf den großen Kolben wirkt, entspricht gerade der Gewichtskraft des Wagens. Es ergibt sich somit für die gesucht Kraft
.
Ist das nicht erstaunlich? Um einen Wagen mit einer Masse von zu heben, musst du nur eine Kraft von etwa 
aufwenden. Das entspricht ungefähr das Heben eines Objektes der Masse 
.
Anwendungsgebiete
Zum Abschluss schauen wir uns ein paar Lebensbereiche an, wo hydrostatischer Druck eine wesentliche Rolle spielt.
Wir hatten am Anfang das Tauchen erwähnt. An diesem Punkt sollte dir bekannt sein, dass der hydrostatische Druck mit steigender Wasserhöhe ebenfalls steigt. Beim Tauchen macht es sich dadurch bemerkbar, dass du einen umso größeren Druck verspürst, je tiefer du tauscht.
Eine weitere wichtige Anwendung sind Wassertürme. Durch Verwendung von Pumpen füllt man diese mit Wasser. Aufgrund des hydrostatischen Drucks kann sich dann das Wasser auf die Wohnungen verteilen, die tiefer liegen, ohne Verwendung von Pumpen.
Beim Trinken mit einem Strohhalm befördern wir dir die Luft innerhalb des Strohhalms durch das Saugen in unseren Mund. Dadurch reduziert sich der Druck im Strohhalm. Am Boden des Glases ist der hydrostatische Druck höher als im Strohhalm, wodurch die Flüssigkeit über den Strohhalm in unseren Mund gelangt.