Wie leitet man die Kontinuitätsgleichung her?

Die Kontinuitätsgleichung leitet man her, indem man für einen abgegrenzten Kontrollraum die Massenerhaltung als Bilanz formuliert: Bei stationärer Strömung ist die zeitliche Massenänderung im Kontrollraum null, daher ist der einströmende Massenstrom gleich dem ausströmenden. Mit und folgt .

Was ist der Unterschied zwischen Massenstrom und Volumenstrom?

Der Massenstrom gibt an, wie viel Masse pro Zeit durch einen Querschnitt fließt (Einheit: ). Der Volumenstrom gibt an, wie viel Volumen pro Zeit durchfließt (Einheit: ). Beide hängen über die Dichte zusammen: .

Was bedeutet der Punkt über einer Größe wie der Masse oder dem Volumen bei der Kontinuitätsgleichung?

Der Punkt über einer Größe bedeutet die zeitliche Ableitung dieser Größe, also „pro Zeit“. ist deshalb nicht die Masse , sondern die Änderungsrate der Masse und wird als Massenstrom in verwendet. Entsprechend ist die zeitliche Änderung des Volumens und wird als Volumenstrom in genutzt.

Woran erkennt man in Aufgaben, ob man ein Fluid als inkompressibel annehmen darf?

Ein Fluid darf man in Aufgaben als inkompressibel annehmen, wenn die Dichte als konstant behandelt werden kann. Das ist oft der Fall, wenn ausdrücklich „inkompressibel“ oder angegeben ist oder wenn es sich um eine Flüssigkeit wie Wasser bei üblichen Rohrströmungen handelt. Bei Gasen muss die Aufgabe kleine Dichteänderungen nahelegen.

Video

Zurück zum Text

Weiter lernen Empfohlenes passendes Video

Kontinuitätsgleichung

In diesem Beitrag erklären wir dir die Kontinuitätsgleichung (auch bekannt als Konti Gleichung) in der Strömungslehre. Wir leiten die Massen- und Volumenströme her und zeigen den Zusammenhang zur Kontinuitätsgleichung. Ebenso gehen wir auf die Unterscheidung zwischen kompressiblen und inkompressiblen Fluiden ein. Abschließend betrachten wir die Anwendung des Erhaltungssatzes anhand von anschaulichen Beispielen.

Inhaltsübersicht

Kontinuitätsgleichung Strömungslehre Definition

Die Kontinuitätsgleichung der Strömungslehre beschreibt ein Prinzip der Massenerhaltung. Der Massenstrom bei stationärer oder inkompressibler Strömung durch einen Volumenkörper (Stromröhre) bleibt konstant. Die Summe der eintretenden und der austretenden Massenströme ist somit identisch und unabhängig der Querschnitte der durchströmten Stromröhre. Es ändert sich einzig die Strömungsgeschwindigkeit. Deshalb stellt die Kontinuitätsgleichung auch einen Erhaltungssatz in der Strömungslehre dar.

Kontinuitätsgleichung Volumenstrom und Massenstrom

Die Herleitung der Kontinuitätsgleichung kann anhand eines abgegrenzten Kontrollraums, zum Beispiel einer Stromröhre, durch die ein Fluid fließt, vorgenommen werden.

Kontinuitätsgleichung - Stromröhre, Massen- und Volumenstrom — Kontinuitätsgleichung – Stromröhre

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Nach Beantwortung speichern wir deine Antwort, um Studyflix zu verbessern. Mehr dazu erfährst du in unserer Datenschutzerklärung.

Kontiniutätsgleichung Massenstrom

In diese Stromröhre fließt vorne durch den Querschnitt A_1 das Fluid mit einer bestimmten Geschwindigkeit v_1 und einer Dichte $\rho_1$ hinein und am Austrittsquerschnitt A_2 mit der Geschwindigkeit v_2 und der Dichte $\rho_2$ wieder hinaus. Die Massenerhaltung in dem Kontrollvolumen bedeutet, dass der eintretende sowie der austretende Strom gleich groß sein muss. Bezogen auf den Kontrollraum erhält man unter Berücksichtigung des Massengleichgewichts:

$\.m = 0$

Der Punkt auf einer physikalischen Größe entspricht Notation für die Ableitung dieser Größe nach der Zeit. Die Summe aus ein- und austretenden Massenströmen ist demnach gleich Null. Die einströmenden Massenströme sind dabei positiv und die ausströmenden Massenströme negativ definiert, woraus sich obige Gleichung umformen lässt zu:

$\.m_1 = \.m_2$

Die zeitliche Ableitung der Masse $\.m$ ergibt sich aus dem Produkt aus der Dichte $\rho$ und der zeitlichen Veränderung des Volumens $\.V$ :

$\.m =\rho \cdot \.V$

Kontinuitätsgleichung Volumenstrom

Mit folgender Gleichung lässt sich der Volumenstrom berechnen:

$\.V = v \cdot A$

Setzen wir dies in die Gleichung des Massenstroms ein, erhalten wir schlussendlich die Kontinuitätsgleichung in der Strömungsmechanik:

$\rho_1\ \cdot \ v_1\ \cdot \ A_1\ =\rho_2\ \cdot \ v_2\ \cdot \ A_2$

Mit der Kontinuitätsgleichung können die verschiedenen Parameter eines Fluids, welches durch einen definierten Kontrollraum, z.B. eine Rohrleitung fließt, berechnet werden. Sind die Dichte und die Volumina des Fluids am Eintritts- und Austrittsquerschnitt gegeben, kann daraus beispielsweise die Änderung der Fließgeschwindigkeit des Stroms ermittelt werden.

Kompressible und imkompressible Fluide

In der Strömungslehre wird zwischen inkompressiblen und kompressiblen Fluiden unterschieden. Hat ein Druck, der auf ein Fluid wirkt, keinen Einfluss auf die Dichte dieses Fluids, so nennt man dieses Fluid inkompressibel. Inkompressible Fluide sind jedoch nur eine Idealisierung und existieren in der Realität nicht. Die Annahme eines inkompressiblen Fluids vereinfacht viele Berechnungen in der Strömungslehre. Bei imkompressiblen Fluiden gilt:

$\rho_1 = \rho_2$

Womit sich die Kontinuitätsgleichung vereinfacht zu:

$v_1\ \cdot \ A_1\ =\ v_2\ \cdot \ A_2\ \rightarrow\ {\dot{V}}_1={\dot{V}}_2$

Kontinuitätsgleichung Beispiel: Verjüngung einer Rohrleitung

Kontinuitätsgleichung - Berechnungen anhand einer Rohrleitung — Kontinuitätsgleichung – Berechnungen anhand einer Rohrleitung

Gegeben sei eine Verjüngung an einer kreisförmigen Rohrleitung wie im obigen Bild. Das Fluid, welches durch das Rohr fließt, ist Wasser mit der Dichte 997 $\frac{kg}{m^3}$ . Der Massenstrom $\.m_1$ fließt in den Querschnitt A_1 mit dem Radius r_1 = 6 cm und einer Geschwindigkeit von $v_1 = 0,3 \frac{m}{s}$ . Der Massenstrom $\.m_2$ tritt am Ausgangsquerschnitt A_2 mit Radius r_2 = 2 cm wieder heraus. Mit welcher Geschwindigkeit v_2 tritt der Massenstrom aus der Rohrleitung aus? Wie groß sind die Massenströme $\.m_1$ und $\.m_2$ ?

Lösung:

Bei Wasser handelt es sich näherungsweise um ein inkompressibles Fluid, weswegen wir von einer inkompressiblen Strömung ausgehen können. Die Kontinuitätsgleichung vereinfacht sich zu:

$\rho_1\ \cdot \ v_1\ \cdot \ A_1\ =\rho_2\ \cdot \ v_2\ \cdot \ A_2\ =const.$

$\downarrow$

$v_1\ \cdot \ A_1\ =\ v_2\ \cdot \ A_2\ =const.$

Stellen wir die Gleichung nach v_2 um erhalten wir:

$v_2=\ \frac{v_1\cdot A_1}{A_2}$

Die Querschnittsflächen können über die Radien berechnet werden:

$A_1=\ \pi{r_1}^2=\pi\cdot \left(0,06m\right)^2=0,0113m^2$

$A_2=\ \pi{r_2}^2=\pi\cdot \left(0,02m\right)^2=0,00126m^2$

Durch Einsetzen der Werte kann die Austrittsgeschwindigkeit v_2 ermittelt werden:

$v_2=\ \frac{0,3 \frac{m}{s} \ \cdot \ 0,0113m^2}{0,00126m^2}=2,69 \frac{m}{s}$

$\rigtharrow$ Die Austrittsgeschwindigkeit beträgt also $2,69 \frac{m}{s}$ .

Im nächsten Schritt können die Massenströme über die Kontinuitätsgleichung ermittelt werden. Da die Massenströme nach der Kontinuitätsgleichung identisch sein müssen, lässt sich folgender Zusammenhang aufstellen:

$\rho_1\ \cdot \ v_1\ \cdot \ A_1\ =\rho_2\ \cdot \ v_2\ \cdot \ A_2=\ \dot{m}=const.$

$\rightarrow\ \ {\dot{m}}_1=\rho_1\ \cdot \ v_1\ \cdot \ A_1=997\frac{kg}{m^3}\ \cdot 0,3\frac{m}{s}\cdot \ 0,0113m^2=3,38\frac{kg}{s}$

$\rightarrow\ \ {\dot{m}}_2=\rho_2\ \cdot \ v_2\ \cdot \ A_2=997\frac{kg}{m^3}\ \cdot 2,69\frac{m}{s}\cdot \ 0,00126\ m^2=3,38\frac{kg}{s}$

Kontinuitätsgleichung Beispiel: Rohrleitungssystem

Drei Rohrleitungen (1,2 und 3) schließen sich zu einer Sammelleitung (4) zusammen. Gegeben seien folgende Daten:

Mittlere Geschwindigkeit im Rohrleitungssystem: $\bar{v} = 4 \frac{m}{s}$
Volumenströme $\.V_1 = 0,6 \frac{m^3}{s}$ ; $\.V_2 = 0,3 \frac{m^3}{s}$ ; $\.V_3 = 0,4 \frac{m^3}{s}$
Annahme: Wasser als Fluid, stationäre Strömung, Dichte = $997 \frac{kg}{m13}$

Welche Mindestradien müssen die Rohrleitungen haben und wie groß sind die Massenströme an jedem der vier Querschnitte des Rohrsystems?

Lösung:

Als Lösungsansatz dient die Kontinuitätsgleichung für imkompressible Fluide:

$A \cdot \bar{v} = \.V = const. \rightarrow A = \frac{\.V}{\bar{v}}$

Für die Querschnitte ergibt sich:

$A_1=\frac{{\dot{V}}_1}{\bar{v}}=\ \frac{0,6\frac{m^3}{s}}{4\frac{m}{s}}=0,15m^2$

$A_2=\frac{{\dot{V}}_2}{\bar{v}}=\ \frac{0,3\frac{m^3}{s}}{4\frac{m}{s}}=0,075m^2$

$A_3=\frac{{\dot{V}}_3}{\bar{v}}=\ \frac{0,4\frac{m^3}{s}}{4\frac{m}{s}}=0,1m^2$

Wegen der Massenerhaltung gilt:

${\dot{m}}_1+{\dot{m}}_2{\ +\ \dot{m}}_3\ =\ {\dot{m}}_4$

${\dot{V}}_1+{\dot{V}}_2+{\dot{V}}_3={\dot{V}}_4$

Der Austrittsquerschnitt A_4 errechnet sich zu:

$A_4=\frac{{\dot{V}}_4}{\bar{v}}=\frac{1,3\frac{m^3}{s}}{4\frac{m}{s}}=0,325m^2$

Womit die Radien der Rohre ermittelt werden können:

$A=\pi\cdot \ r^2\rightarrow\ r=\sqrt{\frac{A}{\pi}}$

Daraus folgt für die Radien der Leitungen:

$r_1=0,22m\ ;r_2=0,15m\ ;r_3=0,18m\ ;r_4=0,32m$

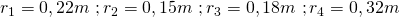
Im letzten Schritt können die Massenströme berechnet werden:

${\dot{m}}_1=A_1\cdot \bar{v}\cdot \rho=0,15\ m^2\cdot 4\frac{m}{s}\cdot 997\frac{kg}{m^3}=598,2\frac{kg}{s}$

${\dot{m}}_2=A_2\cdot \bar{v}\cdot \rho=0,075\ m^2\cdot 4\frac{m}{s}\cdot 997\frac{kg}{m^3}=299,1\frac{kg}{s}$

${\dot{m}}_3=A_3\cdot \bar{v}\cdot \rho=0,1\ m^2\cdot 4\frac{m}{s}\cdot 997\frac{kg}{m^3}=398,8\frac{kg}{s}$

$\rightarrow{\dot{m}}_4=\ {\dot{m}}_1+{\dot{m}}_2{\ +\ \dot{m}}_3=1296,1\frac{kg}{s}$

Gültigkeit der Kontinuitätsgleichung

Die Kontinuitätsgleichung verknüpft die zeitliche Änderung der Dichte einer Erhaltungsgröße mit der räumlichen Änderung ihrer Stromdichte. Die Erhaltungsgrößen kann dabei die Masse, die elektrische Ladung, die Energie, die Wahrscheinlichkeit oder die elektrische Teilchenzahl sein. Demnach findet die Kontinuitätsgleichung in allen Feldtheorien der Physik Anwendung. Sie gilt immer dann, wenn eine ladungsartige mit einer stromartigen Größe verknüpft wird.

Kontinuitätsgleichung — häufigste Fragen

(ausklappen)

Wie leitet man die Kontinuitätsgleichung her?

Die Kontinuitätsgleichung leitet man her, indem man für einen abgegrenzten Kontrollraum die Massenerhaltung als Bilanz formuliert: Bei stationärer Strömung ist die zeitliche Massenänderung im Kontrollraum null, daher ist der einströmende Massenstrom gleich dem ausströmenden. Mit $\dot{m}=\rho\,\dot{V}$ und $\dot{V}=vA$ folgt $\rho_1v_1A_1=\rho_2v_2A_2$ .
Was ist der Unterschied zwischen Massenstrom und Volumenstrom?

Der Massenstrom $\dot{m}$ gibt an, wie viel Masse pro Zeit durch einen Querschnitt fließt (Einheit: $\text{kg}/\text{s}$ ). Der Volumenstrom $\dot{V}$ gibt an, wie viel Volumen pro Zeit durchfließt (Einheit: $\text{m}^3/\text{s}$ ). Beide hängen über die Dichte zusammen: $\dot{m}=\rho\,\dot{V}$ .
Was bedeutet der Punkt über einer Größe wie der Masse oder dem Volumen bei der Kontinuitätsgleichung?

Der Punkt über einer Größe bedeutet die zeitliche Ableitung dieser Größe, also „pro Zeit“. $\dot{m}$ ist deshalb nicht die Masse , sondern die Änderungsrate der Masse und wird als Massenstrom in $\text{kg}/\text{s}$ verwendet. Entsprechend ist $\dot{V}$ die zeitliche Änderung des Volumens und wird als Volumenstrom in $\text{m}^3/\text{s}$ genutzt.
Woran erkennt man in Aufgaben, ob man ein Fluid als inkompressibel annehmen darf?

Ein Fluid darf man in Aufgaben als inkompressibel annehmen, wenn die Dichte als konstant behandelt werden kann. Das ist oft der Fall, wenn ausdrücklich „inkompressibel“ oder $\rho=\text{konstant}$ angegeben ist oder wenn es sich um eine Flüssigkeit wie Wasser bei üblichen Rohrströmungen handelt. Bei Gasen muss die Aufgabe kleine Dichteänderungen nahelegen.

Strömungslehre verstehen

Die Kontinuitätsgleichung ist ein Grundgesetz der Strömungslehre und spielt in vielen technischen Anwendungen eine zentrale Rolle. Wer sich mit Strömungslehre beschäftigt, rechnet mit Größen wie Dichte, Querschnitt und Geschwindigkeit und setzt sie in saubere Gleichungen ein. Wenn du solche Zusammenhänge sicher nutzt, erkennst du schnell, wie sich Ströme in Rohrleitungen anpassen und welche Werte in einem System zusammenpassen. Weitere Videos dazu findest du in unserem Ingenieurwissenschaftenbereich.

zur Videoseite: Kontinuitätsgleichung