Navier Stokes Gleichung
Die Navier Stokes Gleichung ist eine universelle Formel, um die Strömung von Fluiden zu beschreiben. In diesem Beitrag zeigen wir dir die Navier Stokes Gleichung und dessen Herleitung. Außerdem schauen wir, was der Unterschied zwischen kompressiblen und inkompressiblen Fluiden ist und wie man die Navier Stokes Gleichung für bestimmte Systeme vereinfachen kann.
Du willst die Navier Stokes Gleichung verstehen? Dann schau dir doch unser Video an, in dem wir dir alles Wichtige zur Navier Stokes Gleichung erklären.
Inhaltsübersicht
Navier Stokes Gleichung einfach erklärt
In der Strömungsmechanik befasst man sich mit dem physikalischen Verhalten von Gasen und Flüssigkeiten. Diese Stoffe werden als Fluide bezeichnet und werden durch die Navier Stokes Gleichung beschrieben. Bei inkompressiblen Fluiden hängt die Dichte nicht vom Druck ab. Die Navier Stokes Gleichung für inkompressible Fluide ist

Die Gleichung entspricht dem 2. Newtonsches Gesetz
. Die Masse eines Objekts ersetzen wir hierbei durch die Dichte  des Fluids. Das Geschwindigkeitsfeld
des Fluids. Das Geschwindigkeitsfeld  beschreibt die Geschwindigkeit
zu jeder Zeit
beschreibt die Geschwindigkeit
zu jeder Zeit  und an jedem Ort
und an jedem Ort 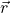 . Der Term
. Der Term  bezeichnet die Änderung des statischen Drucks.
bezeichnet die Änderung des statischen Drucks.  repräsentiert die Viskosität des Fluids und ist ein Maß für die Zähflüssigkeit eines Stoffes. Dies beeinflusst die Reibung des Fluids. Äußere Kräfte wie zum Beispiel die Erdanziehungskraft werden durch den Term
repräsentiert die Viskosität des Fluids und ist ein Maß für die Zähflüssigkeit eines Stoffes. Dies beeinflusst die Reibung des Fluids. Äußere Kräfte wie zum Beispiel die Erdanziehungskraft werden durch den Term  berücksichtigt.
berücksichtigt.
Herleitung Navier Stokes Gleichung
Jetzt wollen wir nachvollziehen, wie sich die Navier Stokes Gleichung aus dem Newtonschen Gesetz ergibt. Um die Strömung eines Volumenelements  mit Masse
mit Masse  beschreiben zu können, gehen wir vom 2. Newtonschen Gesetz aus:
beschreiben zu können, gehen wir vom 2. Newtonschen Gesetz aus:

Dabei bezeichnet  die totale Änderung der Geschwindigkeit
die totale Änderung der Geschwindigkeit

Wir berücksichtigen damit zum einen die zeitliche Änderung von  am selben Ort und die zeitliche Änderung, wenn das Fluid von einem Ort zum anderen strömt. Daher nennt man den Term auch substantielle Beschleunigung. Weil wir die rechte Seite des 2. Newtonschen Axioms nun kennen, benötigen wir jetzt die Kräfte, welche auf ein Volumenelement
am selben Ort und die zeitliche Änderung, wenn das Fluid von einem Ort zum anderen strömt. Daher nennt man den Term auch substantielle Beschleunigung. Weil wir die rechte Seite des 2. Newtonschen Axioms nun kennen, benötigen wir jetzt die Kräfte, welche auf ein Volumenelement  des Fluides wirken. Druckdifferenzen zwischen zwei verschiedenen Orten führen zu einer Druckkraft
des Fluides wirken. Druckdifferenzen zwischen zwei verschiedenen Orten führen zu einer Druckkraft

Wenn du dir das Fluid als Stapelung von Schichten vorstellst, führt die Bewegung der Schichten zu Reibung zwischen den Schichten, wenn die Geschwindigkeit der Schichten unterschiedlich ist. Die Reibungskraft ist

Alle anderen Kräfte zählen zu den äußeren Kräften und schreiben wir allgemein

wobei  die Kraftdichte ist. Wenn wir zum Beispiel die Erdbeschleunigung
die Kraftdichte ist. Wenn wir zum Beispiel die Erdbeschleunigung  mit einbeziehen, erhält man
mit einbeziehen, erhält man

Wenn du im 2. Newtonschen Axiom die Kraft  und die substantielle Beschleunigung
und die substantielle Beschleunigung  einsetzt, führt das auf
einsetzt, führt das auf

Die Navier Stokes Gleichung erhältst du nun durch Division vom Volumenelement  .
.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Navier Stokes Gleichung Kompressible Fluide
Wenn sich die Dichte eines Fluids durch Druckeinwirkung ändert, sprechen wir von kompressiblen Fluiden. Das ist vor allem bei Gasen der Fall. Die Navier Stokes Gleichung muss dann neben der Impulserhaltung auch die Energieerhaltung und die Zustandsgleichung des Gases berücksichtigen. Für kompressible Fluide lautet die Navier Stokes Gleichung

Die Lamé-Zahl  gibt einen Zusammenhang zwischen Dehnung und daraus resultierender Spannung in einem Fluid an und ist eine Materialkonstante. Um zu zeigen, wie sich aus der Navier Stokes Gleichung für kompressible Fluide die Gleichung für inkompressible Fluide ergibt, betrachten wir zunächst die Kontinuitätsgleichung
gibt einen Zusammenhang zwischen Dehnung und daraus resultierender Spannung in einem Fluid an und ist eine Materialkonstante. Um zu zeigen, wie sich aus der Navier Stokes Gleichung für kompressible Fluide die Gleichung für inkompressible Fluide ergibt, betrachten wir zunächst die Kontinuitätsgleichung



Nun erkennt man, dass auf der linken Seite das totale Differential der Funktion  steht
steht
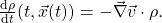
Betrachten wir inkompressible Fluide, so ist die Dichte entlang jeder Teilchenbahn konstant, das heißt

Daraus erhalten wir direkt die Divergenzfreiheit des Geschwindigkeitsfeldes
 denn
denn

Somit haben wir die Navier Stokes Gleichung für inkompressible Fluide direkt aus der Navier Stokes Gleichung für kompressible Fluide abgeleitet

Eulersche Gleichung
Kann man die innere Reibung des Fluids vernachlässigen ( ), vereinfacht sich die Navier Stokes Gleichung zu
), vereinfacht sich die Navier Stokes Gleichung zu

Diese Näherung heißt Eulersche Gleichung und wird zum Beispiel bei der Entwicklung von Flugsystemen oder Rohrströmungen angewendet.
Stokes-Gleichung
Für sehr zähe Fluide kann die Zeitabhängigkeit des Geschwindigkeitsfelds und der Trägheitsterm vernachlässigt werden ( , sodass sich die Navier Stokes Gleichung zu
, sodass sich die Navier Stokes Gleichung zu

vereinfacht. Das ist die Stokes-Gleichung und beschreibt sehr viskose Fluide, wie sie zum Beispiel im Erdmantel vorzufinden sind.
Navier Stokes Gleichung Entdimensionalisierung
Wenn wir die physikalischen Größen in der Navier Stokes Gleichung transformieren, lässt sich eine dimensionslose Gleichung herleiten. Dazu schreiben wir

wobei  eine charakteristische Geschwindigkeit,
eine charakteristische Geschwindigkeit,  eine charakteristische Länge und
eine charakteristische Länge und  eine charakteristische Zeit ist. Setzt man das ein, bekommen wir
eine charakteristische Zeit ist. Setzt man das ein, bekommen wir

Wir vereinfachen diese Gleichung durch Division von  :
:
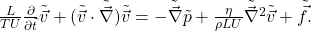
Damit erhalten wir für inkompressible Fluide die dimensionslose Navier Stokes Gleichung

Dabei ist  die Strouhal-Zahl und bezeichnet eine Kennzahl für nichtstationäre Strömungen.
die Strouhal-Zahl und bezeichnet eine Kennzahl für nichtstationäre Strömungen.  heißt Reynolds-Zahl
und beschreibt stationäres Strömungsverhalten. Die beiden Kenngrößen sind von einander abhängig.
heißt Reynolds-Zahl
und beschreibt stationäres Strömungsverhalten. Die beiden Kenngrößen sind von einander abhängig.
Navier Stokes Gleichung Lösung
Die Navier Stokes Gleichung konnte im dreidimensionalen Fall bis heute nicht gelöst werden und zählt zu den Millenium Problemen der Mathematik. Analytisch lässt sich die Navier Stokes Gleichung bislang nur unter vereinfachenden Annahmen lösen. Im zweidimensionalen Fall konnte die Existenz von Lösungen schon erfolgreich untersucht werden. Man kann die Navier Stokes Gleichung jedoch numerisch lösen, was zum Beispiel für die Simulation von Flüssigkeiten genutzt wird.
