Volumenstrom
Was genau ist eigentlich ein Volumenstrom? In diesem Beitrag erklären wir die seine Formel und zeigen dir, wie er mit der Strömungsgeschwindigkeit zusammenhängt.
Damit du diese Thematik leichter verstehst, erklären wir das alles in unserem Video . Also worauf wartest du noch? Schau rein!
Inhaltsübersicht
Volumenstrom Definition
Der Volumenstrom oder Durchfluss ist eine wichtige Komponente in der Strömungsmechanik. Er definiert die Menge eines Mediums in Bewegung.
Das Medium wird innerhalb einer bestimmten Zeitspanne durch einen gewissen Querschnitt transportiert und sozusagen in eine strömende Bewegung versetzt. Man spricht vom Volumenstrom 
oder auch 
.
In diesem Artikel behandeln wir den Volumenstrom bezogen auf inkompressible, also idealisierte Fluide, wie beispielsweise Wasser und arbeiten mit dem Formelzeichen 
.
Volumenstrom Formel
Je nachdem welche Angaben beziehungsweise Ausgangswerte gegeben sind, kann die Berechnung des Volumenstroms variieren.
Die folgenden Absätze behandeln drei verschiedene Methoden und Formeln zur Berechnung des Volumenstroms. Zu beachten ist, dass es sich hierbei immer um idealisierte Angaben und Berechnungen handelt.
Massenstrom und Dichte
Ein direkter Zusammenhang besteht zwischen dem Massenstrom, dem Volumenstrom und der Dichte. Für den Massenstrom haben wir hier ein Video mit allen nötigen Informationen für dich. Zu dieser Thematik ist zusätzlich unser Video zur Kontinuitätsgleichung für dich interessant. Darin wird der Bezug zwischen Volumenstrom und Massenstrom und das Prinzip der Massenerhaltung hergestellt.
Querschnittsfläche und Strömungsgeschwindigkeit
Ist der Querschnitt des durchströmten Rohres und die Strömungsgeschwindigkeit bekannt ergibt sich eine weitere Berechnungsmöglichkeit. Als Alternative für den Querschnitt kann beispielsweise auch der Durchmesser gegeben sein. Mit der passenden Flächenformel kann dementsprechend der Querschnitt ausgerechnet werden.
Damit kann man den Volumenstrom ausrechnen.
oder 
Volumenstrom Einheit
Die SI-Einheit für den Volumenstrom ist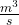 
, wird also über die Grundeinheiten des Volumens und der Zeit gebildet. Eine Alternative bildet sich durch die Nutzung der Einheit Liter 
. Dabei wird bei der Umrechnung von zu 
durch 
geteilt. Ebenfalls oft gebraucht wird die Umrechnung von in 
. In diesem Fall wird mit multipliziert. So entsprechen beispielsweise 
genau 
. Je nach Durchflussmenge wird entweder das Volumen oder die Durchflusszeit in der Einheitenrechnung umgeformt. So werden kleine Durchflussmengen oft in 
und ein großer Volumenstrom in 
angegeben.
Volumenstrom und Wärmestrom
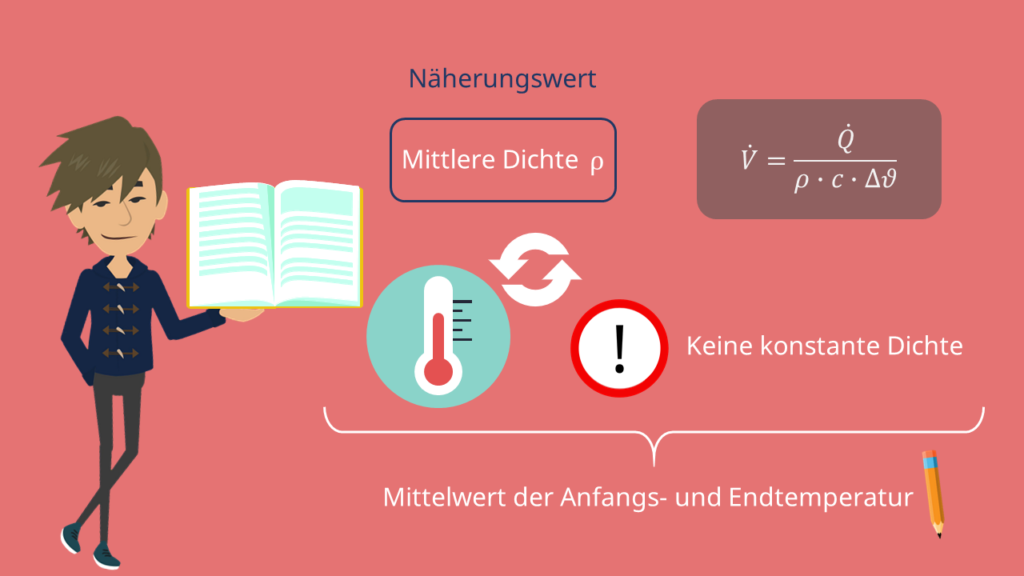
Einen anderer Ansatz zur Berechnung des Volumenstroms bietet die Thermodynamik. Dabei wird der Volumenstrom über den Wärmestrom 
berechnet. Um diese Vorgehensweise zu nutzen sind zusätzlich die mittlere Dichte 
, die spezifische Wärmekapazität 
und die resultierende Temperaturdifferenz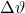 
nötig. Schau dir doch unser Video zur spezifischen Wärmekapazität
an, wenn du nicht mehr genau weißt, was das ist. Da über den zeitlichen Verlauf durch die Temperaturänderung keine konstante Dichte gegeben ist, ist eine zusätzliche Berechnung notwendig.
Formel Volumenstrom und Wärmestrom
Dabei berechnet man die mittlere Temperatur der gegebenen Temperaturunterschiede und liest die, zur Temperatur passende, Dichte aus einer Tabelle aus und erhält die mittlere Dichte. Diese Berechnungsmethodik ist vor allem ein Teil der Auslegung von Heizungsanlagen.
Zu dieser Berechnung gibt es auch noch eine Vereinfachung. Dabei erfolgt eine Zusammenfassung der spezifischen Wärmekapazität und der Dichte. Diese Vorgehensweise gilt aber lediglich als Näherung, da die genaue Dichte nicht beachtet wird.
Die Zusammenfassung der beiden Werte ergibt einen Faktor von 
für 
und 
.
Somit erfolgt eine Umformung der Ausgangsformel zur Berechnung des Volumenstroms.
Es gilt zu beachten, dass diese Näherung nur für Wasser gilt.
Beispiel Volumenstrom berechnen über Wärmestrom
Nehmen wir als eine Beispielsituation doch gleich einmal ein Heizungssystem. Dabei wird warmes Wasser durch die Heizkörper und Heizungsrohre gepumpt und gibt die Wärme an die Umgebung ab, man spricht von einem Wärmetauscher . Bei der Berechnung ist die Kontrolle der Einheiten ein wichtiges Element.
Wärmestrom der Heizung: 
Vorlauftemperatur 
: 
Rücklauftemperatur 
: 
Temperaturdifferenz aus Vor- und Rücklauftemperatur: 
spezifische Wärmekapazität von Wasser:
Dichte von Wasser bei 
: 
Eingesetzt in die Formel zur Volumenstromberechnung über den Wärmestrom ergibt sich folgende Gleichung.
Somit ergibt sich ein Volumenstrom 
für das betrachtete Heizsystem.
Strömungsgeschwindigkeit berechnen
Die Formeln und Einheiten des Volumenstroms kennst du bereits. In der Strömungsmechanik kannst du damit weitaus mehr berechnen, als den Volumenstrom an sich – nämlich beispielsweise der Massenstrom oder die Strömungsgeschwindigkeit. Und wie genau man die Strömungsgeschwindigkeit berechnen kann und was genau du dabei berücksichtigen musst, siehst du in unserem nächsten Video !
Strömungsgeschwindigkeit einfach erklärt
Die Strömungsgeschwindigkeit, auch Fließgeschwindigkeit oder Flussgeschwindigkeit, ist die Geschwindigkeit des Fluids im Betrachtungsbereich. Dabei wird zwischen der Strömungsgeschwindigkeit einzelner Teilchen und der mittleren Strömungsgeschwindigkeit unterschieden. Das ist wichtig, da die Strömungsgeschwindigkeit bei laminaren Strömungen über den Querschnitt nicht immer konstant ist. Deswegen wird mit Hilfe der Integrationsrechnung die mittlere Strömungsgeschwindigkeit beschrieben. Als Formelzeichen nutzen wir ein 
, wobei das 
genauso üblich ist.
So ist beispielsweise die Fließgeschwindigkeit eines Fluids in einem Rohr dessen mittlere Strömungsgeschwindigkeit. Sie ist unter anderem ein Teil der Bernoulli-Gleichung, einer der Grundsteine der Strömungsmechanik. Falls du die Bernoulli-Gleichung noch nicht kennst oder sie dir nochmals ins Gedächtnis rufen möchtest haben wir hier bereits das passende Video für dich.
Die Strömungsgeschwindigkeit besitzt die SI-Einheit 
.
Durch eine Venturi-Düse lässt sich die Strömungsgeschwindigkeit messtechnisch ermitteln. Dabei wird über den maximalen dynamischen und minimalen statischen Druck über die Bernoulli-Gleichung die Fließgeschwindigkeit berechnen.
Die Strömungsgeschwindigkeit besitzt einen großen Einfluss auf die Reynolds – und Froude-Zahl, da beide geschwindigkeitsabhängige Kenngrößen sind. Diese sind wichtige Kennzahlen in der Thermodynamik und der Strömungsmechanik.
In der Praxis haben sich Richtwerte für die Strömungsgeschwindigkeit etabliert. Dabei spielen unter anderem die Leitungsart, das Medium und das Leitungsmaterial eine Rolle.
Beispiel 1
Ein Rohr mit einem Innendurchmesser von 3,0 cm soll pro Minute 20 Liter Wasser befördern. Mit welcher mittleren Strömungsgeschwindigkeit muss das Wasser fließen und welcher Volumen- und welcher Massenstrom ergibt sich dabei?
Analysieren wir zuerst einmal unsere Angaben. Gegeben haben wir einen Innendurchmesser 
. Daraus können wir bereits den Rohrquerschnitt 
berechnen.
Als Nächstes wissen wir, dass 20 Liter Wasser pro Minute durch das Rohr fließen müssen. Das klingt ganz nach dem Volumenstrom.
Nutzen wir nun die Formel aus dem Beitrag zum Volumenstrom ergibt sich folgende Gleichung mit eingesetzten Werten.
-> 
Unser Ziel ist ein Ergebnis mit 
, was mit der richtigen Einheitenrechnung erreicht werden soll.
Als letzten Punkt möchten wir noch den Massenstrom ausrechnen. Aus der Kontinuitätsgleichung ergibt sich der Zusammenhang von Massenstrom, Volumenstrom und Dichte.
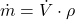
Die Dichte ist in der Aufgabenstellung nicht gegeben. Üblicherweise nimmt man in solchen Fällen eine Temperatur von 
an und schlägt den Dichtewert in Tabellenbüchern nach. Somit ergibt sich eine Dichte von 
. Damit hat man alle nötigen Angaben und kann den Massenstrom berechnen.
Beispiel 2
Versuchen wir uns an einer weiteren Aufgabe.
Mithilfe einer Hydraulikpumpe wird ein kontinuierlicher Strom von 30 Liter pro Minute durch ein Rohr gepumpt. Dabei herrscht eine mittlere Strömungsgeschwindigkeit von 
. Welchen Durchmesser muss das Rohr mindestens besitzen?
Wir haben einen Volumenstrom und eine Strömungsgeschwindigkeit gegeben. Der Zusammenhang mit dem Querschnitt sollte dir mittlerweile bekannt sein.
Aus dem Querschnitt können wir den Durchmesser berechnen.
Jetzt weißt du, dass du ein Rohr oder einen Schlauch mit einem Innendurchmesser von mindestens 12,6 mm benötigst und kannst dir im nächsten Baumarkt das Passende heraussuchen. Dabei musst du auf die richtige Angabe achten. Eine Bemaßung von Rohren erfolgt üblicherweise in Zoll. Hast du nun deinen Durchmesser kannst du dir die passende Zollangabe aus Tabellenbüchern auslesen und das nächstgrößere Rohr kaufen.