Bernoulli-Gleichung
Dieser Artikel behandelt die Bernoulli-Gleichung. Dabei wird erläutert, wo das Gesetz von Bernoulli Anwendung findet, wie man es herleitet und wie die Bernoulli-Gleichung mit der Energieerhaltung zusammenhängt. Aber das ist schon wieder so viel Text zu lesen, geht das nicht einfacher? Ja, geht es! Unser Video erklärt dir die Bernoulli-Gleichung anschaulich innerhalb kürzester Zeit!
Inhaltsübersicht
Bernoulli-Gleichung Definition
Die Bernoulli-Gleichung der Strömungslehre besagt, dass die spezifische Energie von Teilchen in einer Stromröhre nach dem Energieerhaltungssatz konstant bleibt. Passiert das Teilchen die Stromröhre, ändern sich zwar die Energieanteile, die Summe aus potentieller , kinetischer und Druckenergie bleibt jedoch konstant. Gültigkeit hat die Bernoulli-Gleichung bei stationären, reibungsfreien und inkompressiblen Strömungen. Im Falle einer stationären, reibungsfreien Strömung in einem Kontrollvolumen (z.B. Stromröhre) ist die Summe aus potentieller Energie, kinetischer Energie und Druckenergie konstant:


Unter Zuhilfenahme von  ergibt sich für jeden beliebigen Abschnitt in der Röhre:
ergibt sich für jeden beliebigen Abschnitt in der Röhre:

Da das Volumen  der Flüssigkeit ebenfalls konstant ist, dividiert man durch das Volumen
der Flüssigkeit ebenfalls konstant ist, dividiert man durch das Volumen  und erhält das Gesetz von Bernoulli:
und erhält das Gesetz von Bernoulli:

Bernoulli-Gleichung Herleitung
Um die Bedeutung und Anwendung des Satz von Bernoulli nachvollziehen zu können, ist es sinnvoll, die Herleitung anhand eines konkreten Beispiels vorzunehmen. In den anderen Videos der Playlist wurde bereits erklärt, wie sich Drücke in einem ruhig stehenden Behälter verhalten. Noch einmal kurz zur Wiederholung: Der Druck hängt vom Umgebungsdruck bzw. allgemein vom Druck auf eine Fläche und der Höhe bzw. Tiefe ab. Die Gleichung dafür lautet:

Da wir jetzt aber ein bewegtes Fluid betrachten, muss man noch etwas zusätzlich berücksichtigen. Im letzten Video wurde mit der Kontinuitätsgleichung bereits die erste Grundgleichung der dynamischen Fluide behandelt. Dieser Beitrag deckt die zweite Gleichung ab: Die Bernoulli-Gleichung. Diese Gleichung beruft sich auf die Energieerhaltung in einem Kontrollvolumen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Bernoulli-Gleichung: Teilchen in einer Stromröhre
Hier ist ein kleines Teilchen dargestellt, das sich entlang einer Stromlinie bewegt. Diese Stromlinie läuft durch ein Rohr, welches das Kontrollvolumen ist. Das Teilchen bewegt sich durch die Einwirkung verschiedener Kräfte. Das sind die Kräfte, die durch den Druck auf die Fläche A1 und auf die Fläche A2 sowie durch die Erdschwere hervorgerufen werden. Werden diese Kräfte addiert, summieren sie sich zur Gesamtkraft, die für die Bewegung verantwortlich ist. Diese lässt sich mit  ausdrücken. Und da, wie bereits erwähnt, die Gesamtkraft aus der Summe der Einzelkräfte entsteht, kann der Zusammenhang mit folgender Gleichung ausgedrückt werden:
ausdrücken. Und da, wie bereits erwähnt, die Gesamtkraft aus der Summe der Einzelkräfte entsteht, kann der Zusammenhang mit folgender Gleichung ausgedrückt werden:

Herleitung der Bernoulli-Gleichung durch Umformung
Für  kannst du dabei
kannst du dabei  schreiben.
schreiben.  steht dabei für die Länge des Teilchens im Kontrollvolumen. Da die Querschnittsfläche des Teilchens überall gleich ist, sind A1 und A2 gleichzusetzen. Die Formel vereinfacht sich zu:
steht dabei für die Länge des Teilchens im Kontrollvolumen. Da die Querschnittsfläche des Teilchens überall gleich ist, sind A1 und A2 gleichzusetzen. Die Formel vereinfacht sich zu:

Durch Ausmultiplizieren des Terms in der Klammer mit der Fläche  und Kürzungen ergibt sich:
und Kürzungen ergibt sich:

Der Ausdruck  wird durch das Volumen
wird durch das Volumen  ersetzt, wodurch sich die Gleichung weiter vereinfacht:
ersetzt, wodurch sich die Gleichung weiter vereinfacht:

Der Faktor f bezieht sich auf die Volumenkraft der Erdschwere und lässt sich am besten anhand einer Skizze veranschaulichen.
Da die Kraft in z-Richtung für die Berechnung interessant ist, wird der Sinus benötigt. Also  . Da
. Da  ist, kannst für f auch
ist, kannst für f auch  geschrieben werden. Wird f nun wieder in die Grundgleichung eingesetzt, ergibt sich:
geschrieben werden. Wird f nun wieder in die Grundgleichung eingesetzt, ergibt sich:

Die Beschleunigung lässt sich auch mit der Geschwindigkeit in Abhängigkeit der Zeit beschreiben, also  . Wird dieser Term mit
. Wird dieser Term mit  erweitert, so kann er so umgeformt werden, dass die Geschwindigkeit vom Weg abhängt. Man erhält also
erweitert, so kann er so umgeformt werden, dass die Geschwindigkeit vom Weg abhängt. Man erhält also 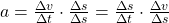 . Da ja
. Da ja  ist, ergibt sich für
ist, ergibt sich für  . Setzt man das wieder in die Hauptgleichung ein, sieht diese so aus:
. Setzt man das wieder in die Hauptgleichung ein, sieht diese so aus:

Bevor das ganze integriert werden kann, muss noch für die Masse  eingesetzt werden. Das Volumen kann daraufhin aus der Gleichung gekürzt werden, womit die zu integrierende Gleichung folgendermaßen lautet:
eingesetzt werden. Das Volumen kann daraufhin aus der Gleichung gekürzt werden, womit die zu integrierende Gleichung folgendermaßen lautet:

Jetzt integriert man nur noch nach dem Weg woraus die fertige Bernoulli-Gleichung resultiert:

Dabei ist  der Anteil vom statischen Druck,
der Anteil vom statischen Druck,  der Druck aus Erdschwere und
der Druck aus Erdschwere und  der dynamische Druck. Der Faktor z ist dabei identisch zur Höhe h.
der dynamische Druck. Der Faktor z ist dabei identisch zur Höhe h.
Energieerhaltung bei der Bernoulli-Gleichung
Der Zusammenhang mit der Energieerhaltung im Kontrollvolumen kann ganz einfach beschrieben werden. Das Teilchen auf der Stromlinie besitzt beim Eintritt in das Kontrollvolumen eine gewisse Bewegungs- und Höhenenergie, die sich während der Bewegung ändern kann. Sie können sich aber nur so weit ändern, dass die Summe der Energie beim Austritt wieder genauso so groß ist wie am Anfang. Also:

Dabei beschreibt  die kinetische Energie und
die kinetische Energie und  die potentielle Höhenenergie.
die potentielle Höhenenergie.
Angenommen die Höhenenergie bleibt gleich, aber die kinetische Energie wird zum Ende hin kleiner. In diesem Fall muss sich auch der Druck beim Durchlaufen des Kontrollvolumens verändern. Dieser muss nämlich dann am Anfang kleiner sein als am Ende. Nur so bleibt die Summe der eintretenden Energien genau so groß wie die Summe der austretenden Energien.
Folgerungen aus der Bernoulli-Gleichung
Der Effekt, dass an einem Ort, an dem die Strömung tendenziell schneller ist, der Druck aber kleiner wird, ist als Bernoulli-Effekt bekannt. Er wird auch hydrodynamisches Paradoxon genannt und kann beobachtet werden, wenn man beispielsweise Luft zwischen zwei parallel angeordneten Papierblättern einbläst. Durch den verringerten Druck im Luftstrom werden die Blätter durch den höheren Umgebungsdruck zusammengepresst. Allgemein ausgedrückt, werden Objekte, die an Strömungslinien von Gasen und Flüssigkeiten angrenzen, in diese hineingezogen.
Bernoulli-Gleichung Anwendung
Der Bernoulli-Effekt wird sich in zahlreichen Anwendungen zu Nutze gemacht. So basieren die Perlatoren (Strahlregler), die am Austritt eines Wasserhahns den Wasserdurchsatz durch Beimischung von Luft reduzieren auf dem Satz von Bernoulli. Ein weiteres Beispiel sind Airbrushpistolen, oder allgemein Druckluftpistolen für Farben und Lacke. Durch den Bernoulli-Effekt wird hierbei die Farbe aus einem Reservoir in den Luftstrom gesogen. In der Chemie wird er auch dafür verwendet, um Gase in Flüssigkeiten aufzulösen. Der Bernoulli-Effekt kann andererseits auch negative Effekte mit sich bringen. So ist er dafür verantwortlich, dass es bei Sturm passieren kann, dass Häuser abgedeckt werden. Dies ist darauf zurückzuführen, dass die Luft sehr schnell über das Dach strömt, wodurch es zu Druckunterschieden zwischen der Außen- und Innenseite des Dachs kommt. Das Dach deckt sich ab.


