Reynoldszahl
Die Reynoldszahl hilft unter anderem bei der Bestimmung der Strömungsart. Wie das funktioniert und mehr erfährst du in diesem Beitrag.
Du hättest eher Lust alles in einem Video erklärt zu bekommen? Dann haben wir eine gute Nachricht: Wir haben zur Reynoldszahl ein eigenes Video, das du dir gerne ansehen kannst.
Inhaltsübersicht
Reynoldszahl einfach erklärt
Die Reynoldszahl ist eine nach dem Physiker Osborne Reynolds benannte Kenngröße, die unter anderem in der Strömungslehre zur Unterscheidung von laminarer und turbulenter Strömung herangezogen wird.
Je nach Bezugsquelle findet man verschiedene Definitionen der Reynoldszahl. Der Unterschied liegt aber darin, welche Größen zusammengefasst werden und welche nicht. Wir geben hier zwei der gängigsten Definitionen.
Die Reynoldszahl ist eine dimensionslose Kenngröße und lässt sich ausrechnen mit
 .
.
Hier ist  das Symbol für die Reynoldszahl,
das Symbol für die Reynoldszahl,  die Dichte des Fluids in
die Dichte des Fluids in  ,
,  die mittlere Strömungsgeschwindigkeit des Fluids
in
die mittlere Strömungsgeschwindigkeit des Fluids
in  relativ zum Körper, in dem es fließt,
relativ zum Körper, in dem es fließt,  die charakteristische Länge des Körpers in
die charakteristische Länge des Körpers in  und
und  die dynamische Viskosität
des Fluids in
die dynamische Viskosität
des Fluids in  .
.
Fasst man die Dichte  und die dynamische Viskosität
und die dynamische Viskosität  zusammen zur kinematischen Viskosität
zusammen zur kinematischen Viskosität
 , dann erhält man eine weitere gängige Darstellung
, dann erhält man eine weitere gängige Darstellung
 .
.
Die kinematische Viskosität besitzt dabei die Einheit  .
.
Übersteigt die Reynoldszahl einen vom Problem abhängigen Wert, die sogenannten kritische Reynoldszahl  , dann ist mit einem Wechsel von laminarer zu turbulenter Strömung zu rechnen. Für eine Rohrströmung wird häufig der kritische Wert auf 2300 gesetzt. Für ideale Flüssigkeiten
ist die Reynoldszahl unendlich, da diese keine Viskosität per Annahme vorweisen.
, dann ist mit einem Wechsel von laminarer zu turbulenter Strömung zu rechnen. Für eine Rohrströmung wird häufig der kritische Wert auf 2300 gesetzt. Für ideale Flüssigkeiten
ist die Reynoldszahl unendlich, da diese keine Viskosität per Annahme vorweisen.
Reynoldszahl Formel
In diesem Abschnitt schauen wir uns die Formel für die Reynoldszahl genauer an. Wir werden dabei zwischen einem zylindrischen Rohr und allgemeinen Körpern unterscheiden. Im Fall des zylindrischen Rohrs gehen wir kurz auf das Experiment von Osborne Reynolds ein.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Zylindrisches Rohr
Osborne Reynolds experimentierte mit gefärbtem Wasser in einem zylindrischen Rohr. Er wollte mit diesem Experiment feststellen, wann der Wechsel einer stationären Strömung von laminarer zu turbulenter Strömung stattfindet.
Dazu hatte er ein gläsernes Zylinderrohr, in der Wasser mit einer veränderbaren Strömungsgeschwindigkeit floss. In diese stationäre Strömung injizierte er gefärbtes Wasser über eine kleinere Röhre in die Mitte der Strömung. Solange die Strömungsgeschwindigkeit des Wassers niedrig war, ließ sich die gefärbte Wasserschicht entlang der gesamten Länge des großen Rohrs deutlich erkennen. Wurde die Geschwindigkeit erhöht, konnte man ab einem bestimmten Punkt die gefärbte Wasserschicht nicht mehr erkennen. Die Schicht löste sich auf und diffundierte über den gesamten Querschnitt des Wassers im großen Rohr. An diesem Punkt geschah der Wechsel von laminarer zu turbulenter Strömung.
Für das zylindrische Rohr entspricht die charakteristische Länge  gerade dem Durchmesser des Rohrs. Häufig wird stattdessen auch der Radius
gerade dem Durchmesser des Rohrs. Häufig wird stattdessen auch der Radius  verwendet und man schreibt für die Reynoldszahl
verwendet und man schreibt für die Reynoldszahl
 .
.
In diesem Fall wird die kritische Reynoldszahl  auf 2300 gesetzt. In der Praxis erwartet man dann eine laminare Strömung, wenn die Reynoldszahl kleiner als 2000 ist. Für Reynoldszahlen zwischen 2000 und 4000 ist die laminare Strömung aufgrund von Turbulenzen instabil. Übersteigt die Reynoldszahl den Wert 4000, dann kann man von einer turbulenten Strömung ausgehen.
auf 2300 gesetzt. In der Praxis erwartet man dann eine laminare Strömung, wenn die Reynoldszahl kleiner als 2000 ist. Für Reynoldszahlen zwischen 2000 und 4000 ist die laminare Strömung aufgrund von Turbulenzen instabil. Übersteigt die Reynoldszahl den Wert 4000, dann kann man von einer turbulenten Strömung ausgehen.
Im Fall der laminaren Strömung gilt innerhalb des Rohrs das Gesetz von Hagen-Poiseuille . Wenn du dich für dieses Gesetz mehr interessierst oder mehr über die Strömung eines Fluids durch ein zylindrisches Rohr erfahren möchtest, dann erreichst du unsere Beiträge dazu durch Anklicken der Verlinkungen.
Allgemeiner Körper
Für Körper, die nicht gerade die Form eines Zylinders besitzen (oder durch eine solche angenähert werden können), bestimmt man die Reynoldszahl mit
 .
.
Der Unterschied zum zylindrischen Rohr liegt in der Festlegung der charakteristischen Länge, manchmal auch Bezugslänge genannt. Die genaue Definition dieser Länge hängt von der jeweiligen Problemstellung ab. Dennoch möchten wir ein paar gängige Festlegungen auflisten:
- Strömungskörper: Hier wird die Länge des Körpers in Strömungsrichtung als Bezugslänge gewählt;
- Widerstandskörper: Hier wird die Breite oder Höhe quer zur Strömungsrichtung als Bezugslänge genommen;
- Rohströmungen: Hier wird der Radius oder Durchmesser des Rohres als Bezugslänge gewählt.
Die charakteristische Länge soll das Ausmaß eines – nicht notwendigerweise – dreidimensionalen Körpers charakterisieren und besitzt die Dimension einer Länge. Das Turbulenzverhalten geometrisch ähnlicher Körper ist bei gleicher Reynoldszahl identisch. Dies macht man sich beispielsweise bei der Flugzeugmodellierung zur Nutze, um das Turbulenzverhalten von Flugzeugen anhand kleinerer Modelle zu untersuchen.
Die Reynoldszahl findet aber auch Anwendung in der Wärmelehre . Beispiel hierzu ist die erzwungene Konvektion bei einer längsumströmten Platte oder bei einem querumströmten Körper . Aber auch in der Berechnung des Wärmeübergangskoeffizienten spielt die Reynoldszahl eine Rolle.
Reynoldszahl berechnen
Wir wollen uns hier ein kleines Zahlenbeispiel für den Fall einer Strömung innerhalb eines zylindrischen Rohres anschauen. Das Rohr besitze einen Durchmesser von  . Innerhalb des Rohres fließe Wasser mit einer Geschwindigkeit von
. Innerhalb des Rohres fließe Wasser mit einer Geschwindigkeit von  . Die Dichte des Wassers ist
. Die Dichte des Wassers ist  , die dynamische Viskosität
, die dynamische Viskosität  .
.
Vielleicht wunderst du dich an dieser Stelle über die Einheit der dynamischen Viskosität  , da wir zu Beginn gesagt hatten. dass diese die Einheit
, da wir zu Beginn gesagt hatten. dass diese die Einheit  besitzt. Schauen wir uns das kurz an, um mögliche Verwirrungen zu beseitigen. Die Abkürzung
besitzt. Schauen wir uns das kurz an, um mögliche Verwirrungen zu beseitigen. Die Abkürzung  steht für Pascal und ist die Einheit für den Druck. In SI-Einheiten ausgedrückt sieht das Pascal folgendermaßen aus
steht für Pascal und ist die Einheit für den Druck. In SI-Einheiten ausgedrückt sieht das Pascal folgendermaßen aus
 .
.
Das Produkt aus  und
und  ergibt also gerade
ergibt also gerade  , die Einheit der Viskosität, die wir zu Beginn des Beitrags erwähnt hatten.
, die Einheit der Viskosität, die wir zu Beginn des Beitrags erwähnt hatten.
Wenn wir jetzt alle Zahlenwerte mit entsprechender Umwandlung der Einheiten in die Formel für die Reynoldszahl eines zylindrischen Rohres einsetzen erhalten wir
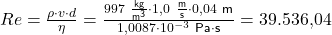 .
.
Die berechnete Reynoldszahl ist daher deutlich größer als 4000 und wir würden eine turbulente Strömung erwarten.
