Kovarianz
Hier erklären wir dir alles zur Kovarianz. Danach kannst du die Kovarianz berechnen und weißt über die Kovarianz Formel und Definition Bescheid. Außerdem kennst du den Unterschied zwischen Kovarianz und Korrelation und die Interpretation ist ein leichtes für dich!
Solltest du also im Durcheinander der verschiedenen Koeffizienten der Statistik also den Überblick verloren haben und dich fragen „Was ist Kovarianz?“ bist du hier genau richtig. Denn wie du das Thema auch ohne großen Leseaufwand erfolgreich meisterst, zeigen wir dir im Video zur Kovarianz!
Inhaltsübersicht
Kovarianz Definition
Die Kovarianz als statistische Größe ist ein nicht standardisiertes Zusammenhangsmaß zur Darstellung linearer Zusammenhänge zwischen zwei kardinalskalierten Variablen. In seltenen Fällen können dir auch die Schreibweisen Covarianz oder Cov(X,Y) begegnen, da sich der Begriff vom englischen Wort covariance ableitet.
Kovarianz Statistik
Die Kovarianz als statistische Messeinheit wird vordergründig zur Überprüfung des Vorliegens eines linearen, monotonen Zusammenhangs zwischen zwei Zufallsvariablen verwendet. Dabei ist es zwingend notwendig zu beachten, dass nur ein linearer Zusammenhang zwischen mindestens kardinalskalierten Variablen bestimmt werden kann, da die Formel sich zum Teil des arithmetischen Mittels der Datensätze bedient. Beispielsweise kann man die Kovarianz anwenden, um den Zusammenhang zwischen der Anzahl der Mitarbeiter in einem Unternehmen und der produzierten Waren (z.B. Joghurt) zu untersuchen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Kovarianzanalyse
Bei der Beschäftigung mit der Kovarianz ist es nicht nur wichtig, die Berechnung gut und schnell zu beherrschen, sondern gleichzeitig auch das gelieferte Ergebnis einzuordnen, analysieren und interpretieren zu können. Nur so kann die Kovarianz als statistisches Zusammenhangsmaß ihr volles Potenzial ausschöpfen und auch konkrete Aussagen zum Zusammenhang zweier Variablen als rechnerischer Beweis unterstützen. Allgemein sollte man sich merken, dass ein positives Ergebnis bei Kovarianzberechnungen einen positiv linearen Zusammenhang indiziert, ein negatives Ergebnis im Gegenzug einen negativ linearen Zusammenhang angibt und bei einem Ergebnis gleich oder nahe 0 zumindest im Hinblick auf den Zusammenhang nicht von Linearität ausgegangen werden kann.
Kovarianz berechnen
Zur Erklärung der praktischen Anwendung der Kovarianz Formel soll mit einer vereinfachten Schreibweise gearbeitet werden, die die Formel in einem Bruch darstellt und in der Praxis gut zu handhaben ist.

Zusammensetzung der Formel:
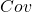 steht für Kovarianz und leitet sich aus dem Englischen von covariance ab.
steht für Kovarianz und leitet sich aus dem Englischen von covariance ab.
 und
und  stehen für die Ausprägung der Zufallsvariablen
stehen für die Ausprägung der Zufallsvariablen
 und
und 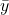 stehen für die Mittelwerte der jeweiligen Datensätze der x- und y-Variable
stehen für die Mittelwerte der jeweiligen Datensätze der x- und y-Variable
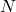 steht für die Größe der Stichprobe und wird durch die Subtraktion mit 1 im Nenner einer Anpassung unterzogen, da die Stichprobe in vielen Fällen nicht der Grundgesamtheit entspricht. Bei der Behandlung einer stichprobenbasierten Datenmenge spricht man auch von der sog. empirischen Kovarianz. Gilt hingegen Stichprobe ist gleich Grundgesamtheit, fand also eine Vollerhebung statt, dann steht nur
steht für die Größe der Stichprobe und wird durch die Subtraktion mit 1 im Nenner einer Anpassung unterzogen, da die Stichprobe in vielen Fällen nicht der Grundgesamtheit entspricht. Bei der Behandlung einer stichprobenbasierten Datenmenge spricht man auch von der sog. empirischen Kovarianz. Gilt hingegen Stichprobe ist gleich Grundgesamtheit, fand also eine Vollerhebung statt, dann steht nur 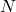 im Nenner.
im Nenner.
Kovarianz Rechenregeln
Als praktische Rechenanleitung, um die Kovarianzberechnung schnell und einfach zu erledigen, folgst du am besten diesen 4 Schritten:
- Zuerst ermittelst du für alle Merkmalsausprägungen deiner X- und Y- Variable die Abweichungen, indem du die Differenz aus den jeweiligen Werten und dem zugehörigen Mittelwert ermittelst
- Während eines zweiten Schrittes bildest du durch Multiplikation der Abweichungen der zusammengehörenden X- und Y- Ausprägungen sogenannte Abweichprodukte.
- Danach summierst du alle Abweichprodukte auf.
- Zum Schluss teilst du, je nachdem ob du mit der kompletten Grundgesamtheit als Fallgröße oder mit einer Stichprobe arbeitest, entweder durch die Anzahl der Fälle (
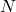 ) oder durch die Anzahl der Fälle minus 1 (
) oder durch die Anzahl der Fälle minus 1 ( ).
).
Kovarianz Beispiel
Um dir nun den Rechenvorgang ausführlich zu erklären, soll ein anschauliches, praktisches Beispiel Abhilfe schaffen: Die Punktetabelle einer Fußballliga. Hierbei handelt es sich um ein stetiges Verteilungsmuster. Untersucht werden soll, ob ein linearer Zusammenhang zwischen der Anzahl der geschossenen Tore (X) und der Anzahl der Punkte ist hier durch unser Vorwissen über Fußball auf jeden Fall ein positiv linearer Zusammenhang.
Stichprobengröße N = 6 (Grundgesamtheit größer, da sich die fiktive Fußballliga hier an der Bundesliga orientiert und daher 18 Mannschaften umfasst, daher im Nenner N-1)
Bevor in die Berechnung gestartet wird, erweitert man die Tabelle, um die Mittelwerte, die Differenzen, das jeweilige Ergebnis aus dem Produkt und den Endwert eintragen zu können.
Kovarianz berechnen Beispiel
Die Berechnung ist dann ganz einfach: Zuerst ermittelt man auf Basis der Tabelle die Mittelwerte für Tore und Punkte, indem die Summe aller Wertausprägungen durch die Anzahl der betrachteten Werte geteilt wird. Für  ergibt sich (6 + 5 + 4 + 1 + 3 + 2) / 6 = 3,5. Für
ergibt sich (6 + 5 + 4 + 1 + 3 + 2) / 6 = 3,5. Für 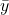 ist der Wert 2,5. Mit den Mittelwerten lassen sich nun die Abweichungen ermitteln. Hier ergibt sich also beispielsweise für Verein 1 die Differenz für X durch 6 – 3,5 = 2,5 und die Differenz für Y durch 6 – 2,5 = 3,5.
ist der Wert 2,5. Mit den Mittelwerten lassen sich nun die Abweichungen ermitteln. Hier ergibt sich also beispielsweise für Verein 1 die Differenz für X durch 6 – 3,5 = 2,5 und die Differenz für Y durch 6 – 2,5 = 3,5.
Es sollte darauf geachtet werden, die Werte nicht durcheinander zu bringen. Die beiden Abweichungen werden im nächsten Schritt multipliziert, man rechnet also 2,5 · 3,5 = 8,75. Somit ist die erste Zeile ausgefüllt. Für die anderen Vereine erfolgt die Berechnung analog. Am Ende muss man nur noch alle Werte der letzten Spalte zusammenrechnen, um auf das Ergebnis von 22,5 zu kommen.
| X=Tore | Y=Punkte | Diff. X | Diff. Y | Produkt | |
| Verein 1 | 6 | 6 | 2.5 | 3.5 | 8.75 |
| Verein 2 | 5 | 6 | 1.5 | 3.5 | 5.25 |
| Verein 3 | 4 | 2 | 0.5 | -0.5 | -0.25 |
| Verein 4 | 1 | 1 | -2.5 | -1.5 | 3.75 |
| Verein 5 | 3 | 0 | -0.5 | -2.5 | 1.25 |
| Verein 6 | 2 | 0 | -1.5 | -2.5 | 3.75 |
| N = 6 |  |
 |
 |
Danach folgt die Übertragung der ermittelten Werte aus der Tabelle auf die Formel. Man setzt also das Zwischenergebnis der Aufsummierung von 22,5 in den Zähler und übernimmt die Stichprobengröße 6 für 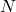 im Nenner, sodass sich am Ende ein Gesamtergebnis von 4,5 ergibt.
im Nenner, sodass sich am Ende ein Gesamtergebnis von 4,5 ergibt.


Das Ergebnis zeigt deutlich, dass der anfangs geäußerte Initialgedanke richtig war und ein positiv linearer Zusammenhang vorliegt. Was dies genau bedeutet und wie du dieses Ergebnis interpretieren solltest, kannst du in einem späteren Abschnitt herausfinden.
Kovarianz Formel
Die reguläre Formel zur Berechnung hast du bereits genauer kennengelernt.

Zusätzlich zu der Kovarianz Formel aus dem Rechenbeispiel können dir alternative Schreibweisen begegnen. Die klassische Formel zur Kovarianzberechnung setzt sich zusammen aus dem Erwartungswert des Produktes der Abweichungen der zwei Zufallsvariablen X und Y von ihrem Erwartungswert E. Sie kommt oft bei diskreten Verteilungen zum Einsatz. Als Formel sieht dieser Zusammenhang so aus:
![Rendered by QuickLaTeX.com Cov\left(X,Y\right)=E\left[\left(X-E(X)\right)\cdot\ \left(Y-E(Y)\right)\right]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8aba594afb20eff07b55d9dcbb4f6d07_l3.png)
Diese Formel wird besonders dann herangezogen, wenn in der Berechnung zwischen stetiger und diskreter Verteilung unterschieden werden soll. Vor allem bei diskreten Verteilungen, unter die zum Beispiel Urnenziehungen oder Würfelexperimente fallen, ist es wichtig in der Berechnung über die Erfahrungswerte zu gehen, um die Wahrscheinlichkeiten (p) mit einzukalkulieren.
Über den sogenannten Verschiebungssatz lässt sich diese Formel durch grundlegende Umformung deutlich vereinfachen, sodass sie zur Veranschaulichung der Zusammenhänge, die über Kovarianzberechnungen festgestellt werden können, beitragen kann.
Verschiebungssatz:
![Rendered by QuickLaTeX.com Cov\left(X,Y\right)=\ E\left[\left(X-E\left(X\right)\right)\cdot\left(Y-E\left(Y\right)\right)\right]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3ef269e6bc6cd5f85ad2444eee58cd68_l3.png)
![Rendered by QuickLaTeX.com Cov\left(X,Y\right)=\ E\left[\left(XY-XE\left(Y\right)-YE\left(X\right)+E\left(X\right)E\left(Y\right)\right)\right]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-24e1d1ba776f948b4674c56bd551fe46_l3.png)


Die Auflösung der Formel durch Multiplikation führt schrittweise zu einer vereinfachten Formel als Endprodukt, die vor allem ein wesentliches Charakteristikum der Kovarianz verdeutlicht: zwei Zufallsgrößen , die voneinander unabhängig sind, sind nicht kovariant.
Positive Kovarianz
Ergibt sich am Ende deiner Berechnungen eine positive Ausprägung der Kovarianz, so lässt sich davon ableiten, dass hohe Werte der betrachteten X-Variable mit ebenfalls hohen Werten der Y-Variable einhergehen. Gleichzeitig kann eine positive Ausprägung auch bedeuten, dass niedrige Werte der betrachteten X-Variable mit ebenfalls niedrigen Werten der Y-Variable einhergehen.
Ausschlaggebend ist auf jeden Fall, dass sich bei einer positiven Kovarianz die beiden betrachteten Variablen gleichgerichtet bewegen.
Negative Kovarianz
Die möglichen Ergebnisse deiner Berechnungen bewegen sich im Rahmen der reellen Zahlen und können somit auch negativ sein. Eine negative Kovarianz impliziert im Hinblick auf die Variablen, dass sich diese entgegen gerichtet zueinander bewegen. Während als Werte der X-Variable einen hohen (niedrigen) Wert annehmen, entstehen für die Y-Variable im Gegenzug niedrige (hohe) Werte.
Unkorreliertheit
Als Alternative zur positiven und negativen Kovarianz kann immer auch der Fall auftreten, dass das Ergebnis 0 ist. Aus diesem Szenario lässt sich für die Interpretation ableiten, dass die beiden über die Variablen betrachteten Merkmale unkorreliert sind und somit in keinem linearen Zusammenhangsverhältnis stehen. Unkorreliertheit heißt jedoch nicht automatisch, dass auch stochastische Unabhängigkeit besteht, da der Zusammenhang zwar bewiesenermaßen nicht linear ist, aber dafür zum Beispiel exponentiell sein kann.
Kovarianz und Korrelation
Man kann über die Berechnung und Interpretation der Kovarianz wichtige Aussagen über die Richtung und Linearität des Zusammenhangs zweier Variablen tätigen. Die zentrale Schwäche dieser statistischen Größe liegt aber darin, dass keine zuverlässige Einschätzung über die Stärke des Zusammenhangs auf Grundlage der Kovarianz getroffen werden kann.
Standardisierte Kovarianz
An diesem Punkt kommt die Korrelation ins Spiel: durch eine Standardisierung der Kovarianz entsteht die sog. Korrelation, die in einem Wertebereich zwischen -1 und 1 operiert und somit auch die Stärke des linearen Zusammenhangs bestimmen kann. Die Kovarianz wird aus diesem Grund oft nur als Teil oder Basis weiterer Korrelationsberechnungen verwendet.
Kovarianz Korrelation Unterschied
Merke dir also: Korrelation ist standardisierte Kovarianz. Ist nur die Richtung des Zusammenhangs gefragt, ist es vollkommen ausreichend, die Kovarianz zu berechnen. Sollst du zusätzlich jedoch auch eine Aussage über die Stärke des linearen Zusammenhangs treffen, benötigst du hierzu den Korrelationskoeffizienten .
Kovarianzmatrix
Die rechnerische Ermittlung der Kovarianz läuft ausschließlich über die Kombination in Paaren, also mit zwei Zufallsvariablen. Will man jedoch den Zusammenhang zwischen mehr als zwei verschiedenen Variablen betrachten, bedient man sich der Darstellung in einer sogenannten Kovarianzmatrix (auch Varianz-Kovarianz-Matrix).
Im Folgenden siehst du eine beispielhafte Verteilung einer Kovarianzmatrix für drei Zufallsgrößen:


Die Abbildung in der Kovarianzmatrix hilft unterdessen auch, eine wesentliche Charakteristik der Kovarianz zu verstehen: ihre Symmetrie. Da bei der Formel im Zähler die jeweiligen Abweichprodukte aufsummiert werden, spielt die Reihenfolge der Variablen keine Rolle. Die Kovarianzen sind also symmetrisch, was sich durch die Spiegelung der Werte an der diagonalen Varianzachse zeigt (zweite Matrix, von links oben nach rechts unten).






