Video

Quiz

Effektivwert

Wichtige Inhalte in diesem Video

Effektivwert einfach erklärt

Effektivwert Formel

Effektivwerte von Wechselspannungen

Effektivwert berechnen Beispiel

In diesem Beitrag erfährst du, wie die Formel für den Effektivwert aussieht, wie du ihn berechnen kannst und wie die Effektivwerte für wichtige Signalformen aussehen.

Wenn du das Ganze anschaulich erklärt haben willst, schau einfach in unser Video rein.

Inhaltsübersicht

Effektivwert einfach erklärt

im Videozur Stelle im Video springen

Der Effektivwert oder auch im Englischen RMS (root mean square)-Wert gibt für elektrische Wechselspannungen und Wechselströme den Wert an, den eine Gleichspannung, beziehungsweise Gleichstrom haben müsste, um die selbe Wärmeleistung in einem rein ohmschen Verbraucher umzusetzen.

Merke

Eine Gleichspannung von 5V erzeugt in einem Widerstand also die selbe Leistung wie eine Wechselspannung mit einem Effektivwert von 5V. Dabei ist die Berechnung des Effektivwerts abhängig von der Signalform der Wechselspannung (Sinus, Rechteck, Dreieck).

Effektivwert Formel

im Videozur Stelle im Video springen

Im folgenden Stellen wir dir die allgemeine Formel zur Berechnung des Effektivwerts vor und zeigen dir außerdem ihre Lösung für häufige Signalformen.

Effektivwert Formel. Effektivwert, Effektivwert periodische Signale, Effektivwert berechnen — Allgemeine Formel für den Effektivwert

Allgemeine Formel des Effektivwerts

Der Effektivwert der Spannung eines beliebigen kontinuierlichen Signal ergibt sich aus folgender Formel.

$U_{eff}=\sqrt{\frac{1}{T}\int_{0}^{T} u(t)^2 dt}$

Gleiches gilt auch für den Strom:

$I_{eff}=\sqrt{\frac{1}{T}\int_{0}^{T} i(t)^2 dt}$

Mathematisch betrachtet entspricht der Effektivwert also dem quadratischen Mittel. Handelt es sich um ein nicht periodisches Signal muss das Integral strenggenommen über die komplette Signaldauer T erfolgen. In diesem Fall geht die T gegen unendlich(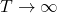 $T \rightarrow \infty$ ).

Effektivwert periodischer Signale

Häufig werden allerdings periodische Signale betrachtet. Für sie ist es ausreichend über eine Periode T zu integrieren um ihren Effektivwert zu erhalten.

$U_{eff}=\sqrt{\frac{1}{T}\int_{t_0}^{t_0+T} u(t)^2 dt}$

$I_{eff}=\sqrt{\frac{1}{T}\int_{t_0}^{t_0+T} i(t)^2 dt}$

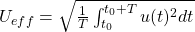
Effektivwerte von Wechselspannungen

im Videozur Stelle im Video springen

Für gängige periodische Signalformen (Sinusspannung, Rechteckspannung, Dreieckspannung) ist die Berechnung über die allgemeine Formel nicht zwingend erforderlich. Der Effektivwert dieser Signale ist von ihrer Amplitude abhängig. Es folgt eine Übersicht über die wichtigsten Wechselspannungen.

Effektivwert, Effektivwert Rechteck, Effektivwert Dreieck, Effektivwert Sägezahn, Effektivwert berechnen — Effektivwert von Rechtecks, Dreiecks und Sägezahn Signalen

Sinusspannung

Für eine Sinusspannung ergibt sich der Effektivwert aus der Amplitude beziehungsweise dem Spitzenwert $\hat{U}$ .

$U_{eff}=\frac{\hat{U}}{\sqrt{2}}$

Symmetrische Rechteckspannung

Für eine periodisches symetrische Rechteckspannung entspricht der Effektivwert der Amplitude beziehungsweise dem Spitzenwert $\hat{U}$ :

$U_{eff}=\hat{U}}$

Dreieckspannung

Für eine Dreieckspannung ergibt sich der Effektivwert aus der Amplitude beziehungsweise dem Spitzenwert $\hat{U}$ .

$U_{eff}=\frac{\hat{U}}{\sqrt{3}}$

Sägezahnspannung

Für eine Sägezahnspannung ergibt sich der Effektivwert aus der Amplitude beziehungsweise dem Spitzenwert $\hat{U}$ .

$U_{eff}=\frac{\hat{U}}{\sqrt{3}}$

Pulssignal/Rechteckssignal

Effektivwert, Effektivwert Puls, Effektivwert Rechteck, Effektivwert berechnen — Effektivwert eines gepulsten Rechtecksignals

Für ein Pulssignal der Amplitude $\hat{U}$ und dem Duty Cycle beziehungsweise Taskgrad D ergibt sich der Effektivwert als.

$U_{eff}= \hat{U} \cdot \sqrt{D}$

Effektivwert berechnen Beispiel

im Videozur Stelle im Video springen

In diesem Beispiel wird der Effektivwert einer weniger häufig vorkommenden Spannungsverlaufs ermittelt. Hier ist es wichtig darüber klarzuwerden, dass die Funktion dieses Spannungsverlaufs abschnittsweise definiert werden kann.

Effektivwert Beispiel, Effektivwert berechnen — Effektivwert Beispiel

In diesem Fall können die beiden Abschnitte durch Geradengleichungen beschrieben werden:

$u(t)=\begin{cases} \frac{20V}{T} \cdot t , & 0 \leq t \leq \frac{T}{2}} \\ \frac{-10V}{T} \cdot t , & \frac{T}{2} \leq t \leq T \end{cases}$

Im ersten Schritt wird die allgemeine Berechnungsformel angesetzt.

$U_{eff}=\sqrt{\frac{1}{T}\int_{0}^{T} u(t)^2 dt}$

Bei Spannungsverläufen die Abschnittsweise definiert werden können, ist es sinnvoll auch das Integral abschnittsweise zu bilden. Mit dieser Überlegung folgt:

$U_{eff}=\sqrt{\frac{1}{T}\int_{0}^{T} u(t)^2 dt}=\sqrt{\frac{1}{T} \left( \int_{0}^{\frac{T}{2}} \left( \frac{20V}{T}\cdot t \right)^2 dt + \int_{\frac{T}{2}}^{T} \left( \frac{-10V}{T}\cdot t \right)^2 dt} \right)$

Nach dem Quadrieren der Klammern ergibt sich:

$U_{eff}=\sqrt{\frac{1}{T} \left(\int_{0}^{\frac{T}{2}} \frac{400V^2}{T^2}\cdot t^2 dt + \int_{\frac{T}{2}}^{T} \frac{100V^2}{T^2}\cdot t^2 dt} \right)$

An dieser Stelle können die Integrale gelöst werden:

$U_{eff}= \sqrt{\frac{1}{T} \left(\left[\left \frac{400V^2}{3T^2}\cdot t^3\right]_0^\frac{T}{2} + \left[\left\frac{100V^2}{3T^2}\cdot t^3\right]_\frac{T}{2}^T } \right) }$

Nach Einsetzten der Integrationsgrenzen ergibt sich:

$U_{eff}= \sqrt{\frac{1}{T} \left( \frac{400V^2}{3T^2}\cdot \left(\frac{T}{2} \right) ^3 - 0 + \frac{100V^2}{3T^2}\cdot T^3 - \frac{100V^2}{3T^2}\cdot \left( \frac{T}{2} \right)^3 \right) }$

$= \sqrt{\frac{1}{T} \left( \frac{400V^2}{3T^2}\cdot \frac{T^3}{8} -0 + \frac{100V^2}{3T^2}\cdot T^3 - \frac{100V^2}{3T^2}\cdot \frac{T^3}{8} \right)}$

Nun können die einzelnen Brüche multipliziert und T gekürzt werden:

$U_{eff}= \sqrt{\frac{1}{T} \left( \frac{400V^2 T}{24} -0 + \frac{100V^2 T}{3} - \frac{100V^2 T}{24}\right) }\\ = \sqrt{ \frac{400V^2 }{24} -0 + \frac{100V^2 }{3} - \frac{100V^2 }{24}}$

Im letzten Schritt können die Brüche einfach addiert werden. Die Einheit des Ergebnisses, in diesem Fall Volt kann als Hinweis für die korrekte Berechnung herangezogen werden.

$U_{eff}= \sqrt{\frac{275}{6}}V =6,77V$

Weitere Anwendungen des Effektivwerts

im Videozum Video springen

Der Effektivwert ist eine zentrale Größe in der Elektrotechnik. Mit ihm kannst du zum Beispiel die Scheinleistung berechnen. Das ist die Leistung, die eine Quelle einem Verbraucher zu Verfügung stellen muss. Du berechnest sie aus dem Produkt der Effektivwerte von elektrischer Spannung und Stromstärke $S = U \cdot I$ .

In unserem Beitrag zur Schein-, Blind- und Wirkleistung erfährst du mehr darüber, was sie ausmacht und wie genau du sie berechnest!

Zum Video: Scheinleistung, Wirkleistung, Blindleistung

zur Videoseite: Effektivwert

Beliebte Inhalte aus dem Bereich Elektrotechnik Grundlagen

Scheinleistung, Blindleistung, Wirkleistung

Phasenverschiebung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .