Zeigerdiagramm
In diesem Artikel lernst du die komplexen Zahlen kennen und wir erklären dir die Impedanz und Phasenverschiebung im Zeigerdiagramm. Um einen Überblick über das Thema zu erhalten schau doch einfach in unser Video rein.
Inhaltsübersicht
Zeigerdiagramm einfach erklärt
Das Zeigerdiagramm in der Elektrotechnik hilft dir dabei das Phasenverhältnis, also den Winkel zwischen Strömen und Spannungen einer Schaltung darzustellen. Es findet vor allem Anwendung in der Wechselstromtechnik, da hier komplexe Zeiger von großer Bedeutung sind. Anstatt Ströme und Spannungen zu berechnen, kannst du sie also direkt mit dem Zeigerdigramm bestimmen.
Komplexe Zahlen
Im den folgenden Abschnitten frischen wir kurz dein Wissen über die komplexen Zahlen auf, da sie als Grundlage für das Verständnis des Zeigerdiagramms dienen. Komplexe Zahlen können auf zwei verschiedene Weisen dargestellt werden. Zum einen in der algebraischen Form und zum anderen in der eulerschen Form.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Algebraische Form
Aus der algebraischen Form kannst du direkt den Realteil und den Imaginärteil einer komplexen Zahl ablesen, da sie aus deren Summe gebildet wird:
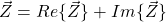
Beispielsweise kannst du dadurch eine komplexe Spannung folgendermaßen angeben:

Eulersche Form
Die eulersche Form wird aus dem Betrag und dem Winkel des Vektors bestimmt den die komplexe Zahl mit dem Ursprung der Gaußschen Zahlenebene aufspannt.

Entsprechend kann eine komplexe Spannung wie folgt ausgedrückt werden:

Zeigerdiagramm
Mit diesem Wissen kannst du nun den Vektor beziehungsweise Zeiger deiner Spannung in einem Zeigerdiagramm einzeichnen.
Bei der Darstellung als Zeiger in einem Zeigerdiagramm gibt es eine Realteil-Achse, üblicherweise die x-Achse, und eine Imaginärteil-Achse. Im kartesischen Koordinatensystem entspricht sie der y-Achse.


Komplexe Impedanz
Bisher haben wir nur Gleichstrom betrachtet, aber aus der Steckdose kommt bekanntlich Wechselstrom. Die Wechselstromlehre wird auch als komplexe Wechselstromlehre bezeichnet, denn der sinusförmige Verlauf von Strom oder Spannung kann als komplexer Zeiger interpretiert werden. Dazu machen wir folgende Annahmen:
- Der Widerstand einer Spule ist
 mit
mit 
- Analog dazu gilt für den Widerstandswert eines Kondensators

- Wie du siehst ist der Widerstandswert nun rein imaginär. Komplexe Widerstände bezeichnet man auch als Impedanz. Für sie gilt: Z=
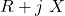
Das ohmsche Gesetz wird in der komplexen Wechselstromlehre damit zu:

Komplexe Zahlen und Impedanz – Beispiel
Um das Rechnen mit komplexen Zahlen und Impedanz zu üben , schauen wir uns ein Beispiel dazu an. Gesucht ist der komplexe Strom für die komplexe Spannung U =  und den komplexen Widerstand Z=j10 Ω .
und den komplexen Widerstand Z=j10 Ω . 
Auch der Strom ist jetzt komplex, denn er besteht aus einem Real- und einem Imaginärteil. Außerdem ist der Imaginärteil unserer Spannung positiv, der des Stromes jedoch negativ
Phasenverschiebung
Spulen und Kondensatoren erzeugen also nicht nur elektrische Felder, sondern bewirken auch, dass das Maximum von Strom und Spannung nicht mehr gleichzeitig auftritt. Das bedeutet eine Phasenverschiebung: Strom und Spannung liegen dann nämlich nicht mehr in Phase. Dazu gibt es zwei Merkregeln:
- Kondensator – Strom eilt vor
- Induktivität – Strom kommt zu spät.
Im Zeigerdiagramm zeigt sich, dass bei Spule und Kondensator die Phasenverschiebung zwischen Strom und Spannung genau 90 Grad ist. Wir fassen nochmal zusammen: Ströme, Spannungen und Widerstände sind komplex und werden als komplexe Zeiger dargestellt. Dazu noch eine Veranschaulichung: Stell dir vor, dass sich die Zeiger mit der Kreisfrequenz Omega bei 50 Hertz, also ungefähr 300 Umdrehungen pro Sekunde gegen den Uhrzeigersinn drehen.



