Ideale Strom- und Spannungsquellen
In diesem Artikel zeigen wir dir was es mit idealen Strom -und Spannungsquellen auf sich hat und erklären dir ihre Anwendung und Kennlinien an einigen Beispielen.
Schau auch am besten gleich in unser Video dazu rein, dort ist alles in kürzester Zeit beschrieben.
Inhaltsübersicht
Ideale Strom und Spannungsquelle einfach erklärt
In vielen Schaltungen und Schaltplänen wirst du ideale Strom und Spannungsquellen antreffen. Tatsächlich gibt es aber keine idealen Quellen dazu. Allerdings ist es oft hilfreich sie zur Modellierung von realen Schaltungen heranzuziehen, da reale Strom und -Spannungsquellen in erster Näherung aus einer idealen Strom bzw. Spannungsquelle und einem Innenwiderstand bestehen.
Stromquelle Schaltsymbol
Zunächst zeigen wir dir, wie die Schaltsymbole solcher Quellen aussehen. Hier siehst du eine ideale Stromquelle:
Die Stromquelle hat zwei Klemmen, welche hier mit 1 und 2 gekennzeichnet sind, an denen sie in einen Stromkreis integriert werden kann. Der Kreis stellt die Stromquelle dar. Charakteristisch für diese Quelle ist der Querstrich in der Mitte des Kreises. Dieser Strich steht immer senkrecht zu den angeschlossenen Leitungen. Außerdem wird der Quellenstrom  eingezeichnet. Teilweise kann auch
eingezeichnet. Teilweise kann auch  geschrieben werden. Dabei handelt sich aber immer um den Strom, den unsere Stromquelle liefert.
geschrieben werden. Dabei handelt sich aber immer um den Strom, den unsere Stromquelle liefert.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
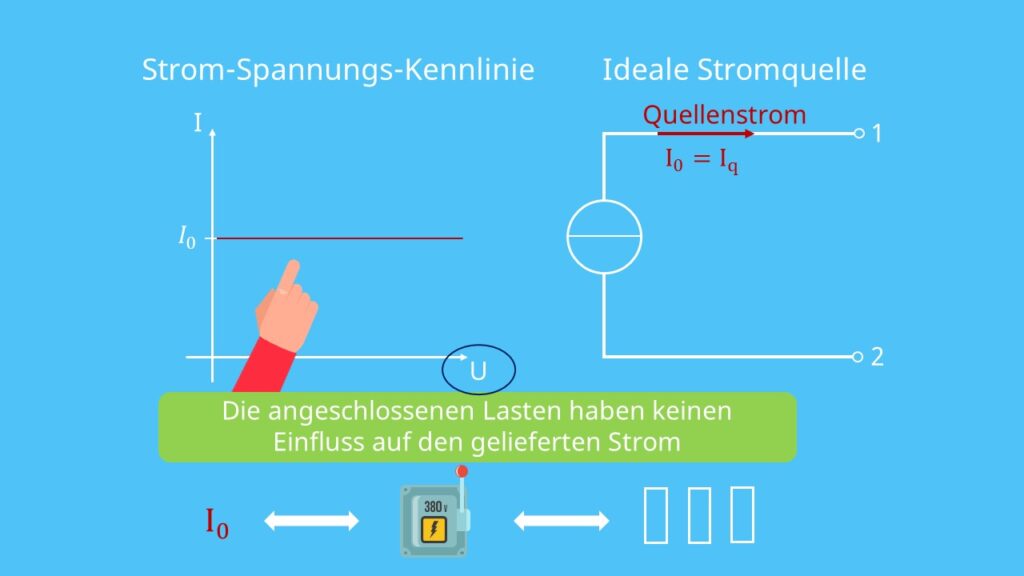
Ideale Stromquelle Kennlinie
Im Folgenden wird die Kennlinie einer idealen Stromquelle betrachtet:
Du siehst, die Stromquelle liefert immer konstant den gleichen Strom  . Das bedeutet, dass die angeschlossenen Lasten keinen Einfluss auf den gelieferten Strom haben. Die anliegende Spannung richtet sich nach dem Quellenstrom und der angeschlossenen Last.
. Das bedeutet, dass die angeschlossenen Lasten keinen Einfluss auf den gelieferten Strom haben. Die anliegende Spannung richtet sich nach dem Quellenstrom und der angeschlossenen Last.
Ideale Stromquelle Beispiel
In einem kleinen Beispiel zeigen wir dir nun die Charakteristiken einer idelen Stromquelle. Wir haben eine ideale Stromquelle mit einem Quellenstrom von  . An diese Quelle hängst du nun einen Lastwiderstand von
. An diese Quelle hängst du nun einen Lastwiderstand von  und danach einen Lastwiderstand von
und danach einen Lastwiderstand von  .
.
Die Spannung, die dann an den jeweiligen Widerständen abfällt, bezeichnen wir als  und
und  . Um sie zu Berechnen nutzt du die Tatsache, dass
. Um sie zu Berechnen nutzt du die Tatsache, dass  durch die angeschlossene Last fließt und konstant ist. Daher kann hier das Ohmsche Gesetz genutzt werden:
durch die angeschlossene Last fließt und konstant ist. Daher kann hier das Ohmsche Gesetz genutzt werden:

Du setzt den Wert  für
für  ein und kannst
ein und kannst  berechnen. Dabei setzt du für
berechnen. Dabei setzt du für 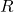 den Wert
den Wert 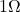 ein und für
ein und für  den Wert
den Wert  . Somit erhältst du für
. Somit erhältst du für 
 und für
und für 
 .
.
Ideale Spannungsquelle Schaltsymbol
Bei einer idealen Spannungsquelle sind die Zusammenhänge sehr ähnlich, wie bei der idealen Stromquelle. Im Folgenden ist das Symbol einer idealen Spanungsquellen zu sehen.
Wie die Stromquelle, wird die ideale Spannungsquelle mit einem Kreis dargestellt. Lediglich der Strich im Kreis ist nun mit den angeschlossenen Leitungen verbunden, quasi durchgezogen. Die Quellenspannung  zeichnet man dabei mit einem Pfeil neben die Spannungsquelle. Diese Spannung liefert unsere Spannungsquelle konstant. An den Punkten 1 und 2 hängt dann die angeschlossene Last.
zeichnet man dabei mit einem Pfeil neben die Spannungsquelle. Diese Spannung liefert unsere Spannungsquelle konstant. An den Punkten 1 und 2 hängt dann die angeschlossene Last.
Ideale Spannungsquelle Kennlinie
Schauen wir uns auch hier die Strom-Spannungs-Kennlinie an:
Wie du sehen kannst, ist die Quellenspannung konstant und unabhängig vom Strom, den die Quelle für die angeschlossene Schaltung liefern muss. Egal welche Widerstände du an die Spannungsquelle hängst, die Spannung an den Klemmen bleibt immer konstant  . Aber werde dir nochmal klar darüber, dass das nur ein Modell ist und in Wirklichkeit immer Verluste auftreten.
. Aber werde dir nochmal klar darüber, dass das nur ein Modell ist und in Wirklichkeit immer Verluste auftreten.
Beispiel ideale Spannungsquelle
Auch bei der Spannungsquelle wollen wir dir ein kleines Beispiel zeigen. Unsere Spannungsquelle hat eine Quellenspannung von  . Wir schließen zuerst einen
. Wir schließen zuerst einen 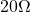 Widerstand an und wollen wissen, wie groß der Strom ist, der in dieser Schaltung fließt. Anschließend machen wir das Gleiche nochmal mit einem
Widerstand an und wollen wissen, wie groß der Strom ist, der in dieser Schaltung fließt. Anschließend machen wir das Gleiche nochmal mit einem  Widerstand.
Widerstand.
Die Widerstände bezeichnen wir als  mit
mit 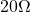 und
und  mit
mit  . Die gesuchten Ströme heißen
. Die gesuchten Ströme heißen  und
und  . Aus der Schaltung geht hervor dass die Spannung an den Lastwiderständen gleich der Quellenspannung
. Aus der Schaltung geht hervor dass die Spannung an den Lastwiderständen gleich der Quellenspannung  sind. Es gilt daher:
sind. Es gilt daher:

Wenn du das Ohmsche Gesetz anwendest, kannst du den Strom im jeweiligen Stromkreis berechnen. Der Strom in der Schaltung ist demnach:

Für  setzt du die Quellenspannung
setzt du die Quellenspannung  von
von  ein. Für
ein. Für 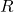 setzt du den Widerstand
setzt du den Widerstand  bzw.
bzw.  ein. Und so erhältst du für den Stromkreis mit dem Widerstand von
ein. Und so erhältst du für den Stromkreis mit dem Widerstand von 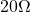 einen Strom von
einen Strom von  und für den mit
und für den mit  einen Strom von
einen Strom von  . Die graphische Lösung sieht dazu so aus:
. Die graphische Lösung sieht dazu so aus: