Drehimpuls
Du möchtest wissen, was es mit dem Drehimpuls und der Drehimpulserhaltung auf sich hat? Das erfährst du in unserem Video und im Beitrag!
Inhaltsübersicht
Drehimpuls einfach erklärt
Mit dem Drehimpuls L beschreibst du den Bewegungszustand eines sich drehenden Körpers. Er ist eine Erhaltungsgröße. Das heißt, der Drehimpuls bleibt immer gleich groß, solange keine Kräfte von außen einwirken. Es liegt also ein abgeschlossenes System vor.
Stell dir dazu einen Kreisel vor, der sich dreht. Ohne Kräfte wie die Reibung würde er sich endlos weiterdrehen, weil der Drehimpuls immer konstant bleibt.
Den Drehimpuls L kannst du mit der Formel Trägheitsmoment J mal Winkelgeschwindigkeit ω berechnen:
L = J ⋅ ω
Das Trägheitsmoment J sagt dir, wie schwer es ist, einen Körper zu drehen. Die Winkelgeschwindigkeit ω beschreibt, wie schnell er sich im Kreis dreht.
Drehimpuls Formel
Um den Drehimpuls L zu berechnen, multiplizierst du sein Trägheitsmoment J mit der Winkelgeschwindigkeit ω.
L = J ⋅ ω
Weil der Drehimpuls und die Winkelgeschwindigkeit Vektoren sind, die senkrecht zur Ebene des sich drehenden Körpers verlaufen, kannst du die Formel auch mit Vektoren schreiben:

Das Trägheitsmoment J sagt dir, wie schwer es ist, die Winkelgeschwindigkeit eines rotierenden Körpers zu verändern. Du berechnest ihn mit J = m ⋅ r² und benutzt dementsprechend die Einheit [kg · m²]. Hierbei ist m die Masse des rotierenden Körpers und r der Radius zwischen dem Mittelpunkt und dem äußersten Punkt des Körpers.
Die Winkelgeschwindigkeit ω gibt an, wie schnell sich der Winkel ( ) in einem Kreis in einer bestimmten Zeit (
) in einem Kreis in einer bestimmten Zeit ( ) verändert. Ihre Einheit ist Rad pro Sekunde [
) verändert. Ihre Einheit ist Rad pro Sekunde [ ], doch du kannst sie laut SI-Einheiten auch als Eins durch Sekunde [
], doch du kannst sie laut SI-Einheiten auch als Eins durch Sekunde [ ] angeben.
] angeben.
Du kannst das Trägheitsmoment und die Winkelgeschwindigkeit auch umformen und erhältst so die Formel für den Drehimpuls L:
L = m · r · v
Also Masse m multipliziert mit Radius r und Geschwindigkeit v.
Multiplizierst du nun die Einheiten von Trägheitsmoment [kg · m²] und Winkelgeschwindigkeit [ ], erhältst du die Drehimpuls Einheit [
], erhältst du die Drehimpuls Einheit [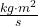 ].
].
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Drehimpulserhaltung
So wie es für den Impuls einen Impulserhaltungssatz gibt, hat auch der Drehimpuls einen entsprechenden Drehimpulserhaltungssatz. Er besagt, dass der Drehimpuls in einem abgeschlossenen System ohne von außen einwirkende Drehmomente immer konstant ist. Das macht sich zum Beispiel ein Eiskunstläufer bei Pirouetten zunutze.
Um sich zu drehen, erfährt zum Beispiel der Eiskunstläufer beim Schwung holen einen Drehimpuls. Wenn er jetzt während der Pirouette seine Arme ausstreckt, wird er langsamer. Das liegt daran, dass der Drehimpuls vom Trägheitsmoment abhängt.
Streckt der Eiskunstläufer nämlich seine Arme (und somit auch die Masse der Arme), wird das Trägheitsmoment größer. Da der Drehimpuls aber immer konstant bleibt, verkleinert sich seine Winkelgeschwindigkeit. Dadurch dreht er sich langsamer. Zieht der Eiskunstläufer die Masse seiner Arme also ganz nah an den Körper, dann wird das Trägheitsmoment kleiner und er dreht sich schneller.
Drehimpulserhaltung Beispiel
Ein Beispiel für den Drehimpulserhaltungssatz ist ein Kinderkarussell auf dem Spielplatz. Das Karussell führt eine Rotationsbewegung um die mittlere Achse aus.
Je weiter sich eine Person (und somit ihre Masse) im Karussell nach außen bewegt, desto größer wird der Radius r und somit auch das Trägheitsmoment J = m⋅ r². Aus der Drehimpulserhaltung folgt, dass der Drehimpuls L = J ⋅ ω in einem abgeschlossenen System immer konstant ist. Das bedeutet, dass sich mit der Vergrößerung des Trägheitsmoments die Winkelgeschwindigkeit ω verringert. Durch den Zusammenhang v = ω ⋅ r wird das Karussell somit langsamer.
Wenn sich die Person nun in Richtung Schwerpunkt bewegt, verkleinert sich der Radius und somit auch das Trägheitsmoment. Die Winkelgeschwindigkeit wird größer und das Karussell wird schneller.
Trägheitsmoment
Wie du jetzt gelernt hast, ist das Trägheitsmoment für den Drehimpuls von entscheidender Bedeutung. Doch was genau kannst du dir darunter vorstellen? Das zeigen wir dir in unserem Video dazu!


