Antiproportionaler Dreisatz
In diesem Beitrag erklären wir dir das Rechnen mit dem antiproportionalen Dreisatz. Anhand von Beispielaufgaben siehst du hier, wie du den antiproportionalen Dreisatz ohne Probleme selbst anwenden kannst!
Inhaltsübersicht
Antiproportionaler Dreisatz einfach erklärt
Der antiproportionale Dreisatz wird auch umgekehrter Dreisatz genannt. Du berechnest dabei Mengen nach der Regel „Je mehr, desto weniger“. Das heißt, je mehr du von der einen Größe hast, desto weniger hast du von der anderen. Diesen Fall findest du beispielsweise, wenn du in der Schule das Klassenzimmer aufräumen musst:
Je mehr Mitschüler dir helfen, desto weniger Zeit benötigt ihr zum Aufräumen.
Das Ergebnis erhältst du immer in drei Schritten – deshalb auch der Name Dreisatz. Wie du bei der Berechnung des antiproportionalen Dreisatzes genau vorgehen musst, erklären wir dir jetzt.
- Beim proportionalen Dreisatz gilt die Regel: „Je mehr desto mehr“. Das bedeutet, wenn die eine Größe mehr wird, wird auch die andere Größe mehr. Diesen Fall hast du zum Beispiel, wenn du im Supermarkt Äpfel kaufst: Je mehr Äpfel du haben möchtest, desto mehr Geld musst du auch bezahlen.
- Beim antiproportionalen Dreisatz lautet die Regel hingegen: „Je mehr desto weniger“. Das heißt, je mehr ich von der einen Größe habe, desto weniger habe ich von der anderen. Diesen Fall findest du beispielsweise, wenn du mit deiner Familie im Auto unterwegs bist. Je höher die durchschnittliche Geschwindigkeit, desto weniger Zeit benötigt ihr für die Fahrt.
Beispiel: Antiproportionaler Dreisatz
Du hast dich bereiterklärt, bei einem Stadtfest den Getränkestand zu betreuen. Dafür musst du erstmal Getränkekisten zum Stand tragen. Das wäre für dich alleine aber ganz schön viel. Daher hast du 8 Freunde gefragt, ob sie dir helfen können. Jeder muss 16 Getränkekisten tragen. Nun haben leider 4 Freunde spontan doch keine Zeit.
Wie viele Getränkekisten muss jeder tragen, wenn nur noch 4 deiner Freunde helfen können?
- Schreibe alles auf, was du über beide Größen weißt
- Berechne das Verhältnis für eine einzige Einheit der einen Größe
- Bestimme nun das Verhältnis zwischen den beiden Größen für eine beliebige Mengenangabe
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Antiproportionaler Dreisatz: Schritt 1
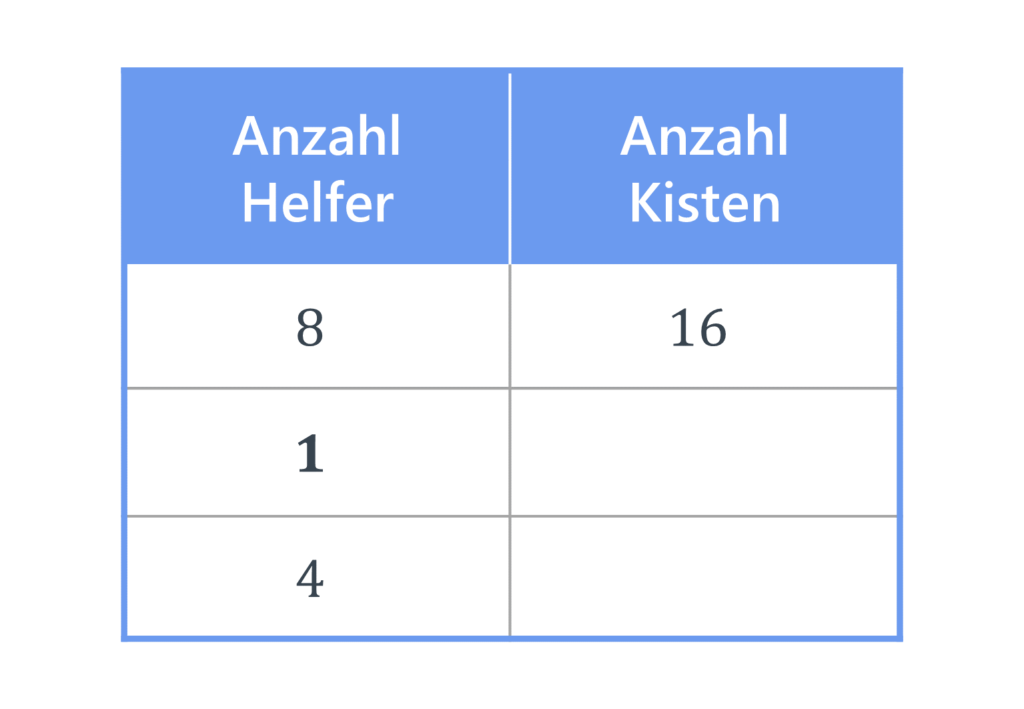
Im ersten Schritt zeichnest du eine Tabelle. Du hast im Beispiel bereits Informationen zu der Anzahl an Helfern und Getränkekisten gegeben. Diese trägst du in die Tabelle ein.
Du weißt, dass bei 8 helfenden Freunden, jeder 16 Getränkekisten tragen muss. Das schreibst du in die erste Zeile der Tabelle. Du möchtest nun das neue Verhältnis an Getränkekisten ausrechnen, wenn nur noch 4 Helfer übrig sind. Das schreibst du in die dritte Zeile.
Da du für diese Rechnung einen Zwischenschritt brauchst, lässt du die zweite Zeile frei.
Antiproportionaler Dreisatz: Schritt 2
Nun folgt der zweite Schritt. Berechne, wie viel von einer einzigen Einheit der einen Größe der anderen Größe entsprechen. Du bestimmst also, wie viele Getränkekisten ein einziger Freund tragen muss, wenn er beim Getränkestand keine Unterstützung hätte. In die zweite Zeile schreibst du daher bei den Helfern eine 1.
Nun musst du noch die Anzahl der Getränkekisten in der zweiten Zeile bestimmen. Bei der Berechnung dieses Werts musst du aufpassen. Denn statt wie beim proportionalen Dreisatz auf beiden Seiten der Tabelle zu teilen, rechnest du jetzt nämlich in einer Spalte geteilt und in der anderen Spalte mal. Das machst du deswegen, weil die eine Größe mehr und die andere Größe weniger wird.
Auf welcher Seite du teilen und auf welcher Seite du malnehmen musst, kannst du an der Tabelle erkennen: In der Spalte der helfenden Freunde steht bereits eine 1.
Um auf diese 1 zu kommen, wurden die 8 Helfer durch 8 geteilt. Da in der Spalte der Helfer geteilt wurde, musst du also die Zahl in der Spalte der Kisten mal 8 nehmen. Wie du siehst, rechnest du aber in beiden Spalten mit der gleichen Zahl mal oder geteilt:
16 · 8 = 128
Ein einzelner Helfer müsste also ganze 128 Getränkekisten tragen!
Antiproportionaler Dreisatz: Schritt 3
Du hast es fast geschafft. Jetzt berechnest du im letzten Schritt nur noch, wie viele Getränkekisten ein Helfer mit insgesamt 4 unterstützenden Freunden tragen müsste. Dafür rechnest du wieder auf einer Seite der Tabelle mal und auf der anderen Seite geteilt.
In der letzten Zeile der Tabelle ist bereits die Zahl 4 eingetragen. Um auf diese Zahl zu kommen, wurde in der Helferspalte also 1 mal 4 gerechnet. Deswegen musst du in der Spalte der Getränkekisten geteilt durch 4 rechnen.
Tipp: Falls das für dich einfacher ist, kannst du dir auch merken, dass du jetzt die Rechenart anwendest, die du im zweiten Schritt in dieser Spalte nicht benutzt hast. Wenn du also zuerst geteilt hast, dann nimmst du jetzt mal und umgekehrt.
Die Zahl, mit der du mal nimmst oder teilst, ist wieder in beiden Spalten dieselbe. Du rechnest also:
128 : 4 = 32
Wenn 4 deiner Freunde dich unterstützen, muss also jeder Helfer 32 Getränkekisten tragen!
Dreisatz Aufgaben
Super! Du weißt jetzt, was ein antiproportionaler Dreisatz ist und wie du ihn berechnest. Möchtest du jetzt dein Wissen noch mit verschiedenen Aufgaben testen? Dann schau in unser Video rein!