Einsetzungsverfahren
In diesem Artikel zeigen wir dir, wie du das Einsetzungsverfahren anwendest. Um das Thema schnell zu verstehen, schau dir unser Video dazu an!
Einsetzungsverfahren Anleitung
Angenommen du hast ein lineares Gleichungssystem gegeben
Wie findest du nun heraus, was x und y ist? Dabei hilft dir das Einsetzungsverfahren. Du löst eine Gleichung nach x oder y auf und setzt sie in die andere Gleichung ein. Gehe dabei wie folgt vor:
Schritt 1: Wähle eine Gleichung aus, die du nach einer Variablen umformst.
Schritt 2: Setze den Wert der Variable in die andere Gleichung ein.
Schritt 3: Berechne die noch enthaltende Variable.
Schritt 4: Setze die in Schritt 3 berechnete Variable in die Gleichung aus Schritt 1 ein und berechne so die übrig gebliebene Variable.
Probe: Setze die ermittelten Werte in die Gleichungen ein und überprüfe, ob die Gleichungen erfüllt sind.
Einsetzungsverfahren Beispiel
Schauen wir uns zum Einsetzungsverfahren das Gleichungssystem von oben an
(I)
(II)
Du sollst nun mithilfe des Einsetzungsverfahrens die Lösung berechnen.
Schritt 1: Wähle eine Gleichung aus, die du nach einer Variablen umformst. Es ist egal, welche Gleichung und welche Variable du auswählst. Wir wählen Gleichung (I) und formen sie nach x um
(I) 
(I) 
(I‘) 
.
Schritt 2: Setze x in Gleichung (II) ein
(II‘) 
(II‘) 
.
Schritt 3: Forme Gleichung (II‘) nach y um, um so den Wert für y zu ermitteln
(II‘) 
.
Schritt 4: Setze 
in Gleichung (I‘) ein und berechne so den Wert für x
(I‘) 
.
Probe: Um zu überprüfen, ob die Lösung und 
richtig ist, setzt du sie in die ursprünglichen Gleichungen (I) und (II) ein
(I) 
(II) 
.
Du siehst, dass beide Gleichungen erfüllt sind. Somit hast du die Lösung richtig berechnet und das Einsetzungsverfahren richtig angewendet.
Einsetzungsverfahren Übungen
Schauen wir uns ein weiteres Beispiel zum Einsetzungsverfahren an. Dafür sei das folgende lineare Gleichungssystem gegeben.
(I) 
(II) 
Schritt 1: Zuerst wählst du eine Gleichung aus, die du nach einer Variablen auflöst. Wenn du zum Beispiel Gleichung (I) nach x umformst, so erhältst du
(I‘) 
.
Schritt 2: Setze x in Gleichung (II) ein und berechne so die Gleichung
x in (II) 
(II‘) 
.
Schritt 3: Um den Wert für y zu bekommen, formst du Gleichung (II‘) nach y um.
(II‘) 
Schritt 4: Jetzt fehlt dir nur noch die Variable x, weshalb du 
in Gleichung (I‘) einsetzt.
y in (I‘) 
Probe: Überprüfe das Ergebnis, indem du und in die ursprünglichen Gleichungen (I) und (II) einsetzt.
(I) 
(II) 
Wie du siehst, sind alle Gleichungen erfüllt, womit du das Einsetzungsverfahren richtig angewendet und die Variablen x und y richtig berechnet hast.
Einsetzungsverfahren: Anzahl der Lösungen
Im nächsten Abschnitt zeigen wir dir anhand von Beispielen, wie viele Lösungen ein lineares Gleichungssystem haben kann, nachdem du das Einsetzungsverfahren angewendet hast.
Keine Lösung
Betrachte als erstes das lineare Gleichungssystem
(I) 
(II) 
.
Darauf wendest du das Einsetzungsverfahren an, das heißt, du formst Gleichung (I) nach x um
und setzt x in Gleichung (II) ein
x in (II) 
.
Damit erhältst du aber mit
eine falsche Aussage, was bedeutet, dass das lineare Gleichungssystem keine Lösung besitzt.
Eindeutige Lösung
Schau dir als nächstes das folgende lineare Gleichungssystem an
(I) 
(II) 
.
Um das Einsetzungsverfahren anzuwenden, formst du lediglich Gleichung (II) nach x um
(II‘) 
Als nächstes setzt du x in Gleichung (I) ein und erhältst
x in (I) 
Setze noch y in (II‘) ein und du erhältst den Wert für x
y in (II‘) 
Damit hast du mit 
und die eindeutige Lösung des linearen Gleichungssystems bestimmt.
Unendlich viele Lösungen
Für diesen Fall sei das folgende lineare Gleichungssystem gegeben
(I) 
(II) 
.
Forme Gleichung (I) nach x um
und setze x in Gleichung (II) ein
x in (II) 
Somit erhältst du mit
eine allgemeingültige Aussage. Das heißt, dass es unendlich viele Lösungen gibt. In diesem Fall kannst du für y jeden beliebigen Wert einsetzen. Somit ist dann die Menge 
die Lösungsmenge des linearen Gleichungssystems.
Weitere Lösungsverfahren linearer Gleichungssysteme
Es gibt verschiedene Verfahren, mit denen du Gleichungssysteme lösen kannst. Schau dir unbedingt auch unsere Videos zu den folgenden Verfahren an:
-
Additionsverfahren
-
Gleichsetzungsverfahren
-
Gaußsches Eliminationsverfahren
- Cramersche Regel
- Lineare Gleichungssysteme Aufgaben .
Einsetzungsverfahren Aufgaben
In diesem Abschnitt geben wir dir zwei Aufgaben mit Lösungen, sodass du das Einsetzungsverfahren üben kannst.
Aufgabe 1: 2 Gleichungen 2 Variablen
Berechne mit dem Einsetzungsverfahren die Lösungen des linearen Gleichungssystems.
(I) 
(II) 
Lösung Aufgabe 1
Forme Gleichung (I) nach y um und erhalte somit die Gleichung
(I‘)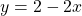 
.
Jetzt setzt du y in Gleichung (II) ein.
y in (II) 
Damit erhältst du
.
Setze nun in Gleichung (I‘) ein.
x in (I‘) 
Damit bekommst du den Wert für y.
Zum Schluss kannst du die Variablen und 
in die Gleichungen (I) und (II) einsetzen, um zu überprüfen, ob du das Einsetzungsverfahren richtig angewendet hast.
(I) 
(II)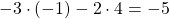 
Da die beiden Gleichungen erfüllt sind, stimmen die beiden Werte für x und y und du hast das Einsetzungsverfahren richtig angewendet.
Aufgabe 2: Einsetzungsverfahren mit 2 Gleichungen
Berechne mit dem Einsetzungsverfahren die Lösungen des linearen Gleichungssystems.
(I) 
(II) 
Lösung Aufgabe 2
Zuerst formst du Gleichung (II) nach x um.
(II‘) 
Nun setzt du x in Gleichung (I) ein, um so eine neue Gleichung zu erhalten, die nur die Variable y enthält.
x in (I) 
(I‘) 
Forme Gleichung (I‘) nach y um und erhalte so den Wert für y.
(I‘) 
Jetzt fehlt nur noch der Wert für x. Dafür setzt du y in die Gleichung (II‘) ein.
y in (II‘) 
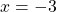
Um zu überprüfen, ob du das Einsetzungsverfahren richtig angewendet hast, setzt du 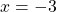und in die Gleichungen (I) und (II) ein und schaust ob die Gleichungen erfüllt sind.
(I) 
(II) 
Da die Gleichungen alle erfüllt sind, hast du das Einsetzungsverfahren richtig angewendet.
