Definitionsmenge bestimmen
Du musst eine Definitionsmenge bestimmen? Hier erfährst du, welche Regeln es dafür gibt und wie du sie auf verschiedene Funktionstypen anwendest.
Inhaltsübersicht
Was ist die Definitionsmenge?
Die Definitionsmenge beschreibt alle Werte, die du für x in eine Funktion einsetzen darfst.
– In die Funktion  darfst du jedes beliebige x einsetzen. Denn egal welche Zahl du einsetzt, du bekommst immer ein Ergebnis. Die Definitionsmenge umfasst daher alle reellen Zahlen.
darfst du jedes beliebige x einsetzen. Denn egal welche Zahl du einsetzt, du bekommst immer ein Ergebnis. Die Definitionsmenge umfasst daher alle reellen Zahlen.
Es gibt aber auch Funktionen, bei denen du nicht alle Zahlen für x einsetzen darfst.
– Bei Brüchen gilt die Regel, dass der Nenner des Bruchs niemals Null sein darf. Bei der Funktion  darfst du für x also nicht 0 einsetzen. Deshalb besteht die Definitionsmenge hier aus allen Zahlen außer 0.
darfst du für x also nicht 0 einsetzen. Deshalb besteht die Definitionsmenge hier aus allen Zahlen außer 0.
Wenn es um die Definitionsmenge geht, überlegst du dir also immer: Welche x-Werte darf ich in die Funktion einsetzen?
Der Definitionsbereich beschreibt alle Zahlen, die du für x in eine Funktion einsetzen darfst. Wenn du alle erlaubten x-Werte in die Funktion einsetzt, bekommst du die entsprechenden y-Werte heraus. Alle diese y-Werte zusammen bilden den Wertebereich, also die Zahlen, die die Funktion annehmen kann.
So schreibst du eine Definitionsmenge auf
Die Definitionsmenge gibst du immer mit dem Zeichen  an. Dahinter beschreibst du genau, welche Zahlen erlaubt sind und welche ausgeschlossen werden müssen.
an. Dahinter beschreibst du genau, welche Zahlen erlaubt sind und welche ausgeschlossen werden müssen.
➡️ Beispiel: Bei der Funktion  darfst du kein x=1 einsetzen, weil der Nenner sonst null wird. In Kurzschreibweise notierst du das so:
darfst du kein x=1 einsetzen, weil der Nenner sonst null wird. In Kurzschreibweise notierst du das so:
![Rendered by QuickLaTeX.com \[ \mathbb{D} = \mathbb{R} \setminus \{1\} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1b7d36038e77f7a21e02ed34f388bdbe_l3.png)
So liest du die einzelnen Zeichen:
-
 steht für die Menge der reellen Zahlen
— also alle Zahlen, die du dir auf einer Zahlengeraden vorstellen kannst (ganze Zahlen, Brüche, Dezimalzahlen usw.).
steht für die Menge der reellen Zahlen
— also alle Zahlen, die du dir auf einer Zahlengeraden vorstellen kannst (ganze Zahlen, Brüche, Dezimalzahlen usw.). - Der Querstrich „∖“ bedeutet „außer“.
- Die geschweiften Klammern {} zeigen die Werte, die nicht erlaubt sind. In diesem Beispiel heißt das also, dass alle reellen Zahlen Teil der Definitionsmenge sind, außer der Wert 1.
Es gibt auch eine zweite Möglichkeit, dieselbe Definitionsmenge aufzuschreiben:
![Rendered by QuickLaTeX.com \[ \mathbb{D} = \{ x \in \mathbb{R} \mid x \neq 1 \} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-18822463c23f8c3f3fcfe7e0b6d02952_l3.png)
Das liest du so: „x gehört zu den reellen Zahlen und ist ungleich 1.“
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Wie bestimmst du die Definitionsmenge für verschiedene Funktionstypen?
Es gibt für jeden Funktionstypen klare Regeln, die du dir für die Definitionsmenge merken kannst. In den nächsten Abschnitten siehst du, wie du sie für die wichtigsten Arten von Funktionen bestimmst.
So bestimmst du die Definitionsmenge für ganzrationale Funktionen
Zu den ganzrationalen Funktionen gehören lineare, quadratische und Funktionen höheren Grades. Sie sind immer gleich aufgebaut und bestehen nur aus Termen mit x, die addiert oder multipliziert werden. Beispiele sind
- lineare Funktionen:

- quadratische Funktionen:

- Funktionen höheren Grades:

Für ganzrationale Funktionen ist die Definitionsmenge ganz einfach zu bestimmen. Denn du darfst jede Zahl für x einsetzen. Die Definitionsmenge ist deshalb immer
![Rendered by QuickLaTeX.com \[ \mathbb{D} = \mathbb{R} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-eceead57bbbef782b9eb82508c85a2dd_l3.png)
Das bedeutet, dass alle reellen Zahlen erlaubt sind — egal ob positiv, negativ, Bruch oder Kommazahl.
So bestimmst du die Definitionsmenge für gebrochenrationale Funktionen
Bei gebrochenrationalen Funktionen gibt es einen wichtigen Unterschied zu ganzrationalen: Sie bestehen immer aus einem Bruch. Grundsätzlich darfst du hier auch alle reellen Zahlen für x einsetzen, es gibt nur eine wichtige Regel: Der Nenner eines Bruchs darf niemals Null sein, denn man darf nicht durch 0 teilen. Du überlegst dir also, bei welchen Zahlen der Nenner der Funktion Null wird. Diese Zahlen gehören nicht zur Definitionsmenge.
Um die Zahlen herauszufinden, bei denen der Nenner gleich Null wird, setzt du den Nenner des Bruchs einfach gleich 0.
➡️ Beispiel:

Der Nenner lautet  . Wenn wir ihn gleich null setzen, ergibt sich:
. Wenn wir ihn gleich null setzen, ergibt sich:

Damit sind die Werte x=2 und x=-2 nicht Teil der Definitionsmenge. Denn wenn du sie in die Funktion einsetzen würdest, würde im Nenner null stehen — das ist nicht erlaubt. Die Definitionsmenge lautet also

Auch im Graphen kannst du die Definitionslücken erkennen.
So bestimmst du die Definitionsmenge für Wurzelfunktionen
Bei Wurzelfunktionen gibt es eine klare Regel. Der Ausdruck unter der Wurzel darf nicht negativ sein. Aus negativen Zahlen kannst du nämlich keine reelle Wurzel ziehen.
Um die Definitionsmenge zu finden, gehst du Schritt für Schritt vor. Zuerst schaust du dir den Term an, der unter der Wurzel steht. Diesen Teil setzt du in eine Ungleichung und schreibst, dass er größer oder gleich null ist. Danach löst du die Ungleichung. Das Ergebnis zeigt dir genau, welche Werte für x erlaubt sind.
Tipp: Wie du Ungleichungen richtig löst, erklären wir dir hier Schritt für Schritt!
➡️ Beispiel 1:

Unter der Wurzel steht x – 2. Diesen Ausdruck setzt du in die Ungleichung. Das heißt, du setzt den Ausdruck größer oder gleich 0:

Um die Ungleichung zu lösen, rechnest du auf beiden Seiten +2.

Damit lautet die Definitionsmenge:

Das bedeutet, dass du alle Zahlen ab 2 einsetzen darfst. Das kannst du hier im Graphen auch nochmal gut sehen.
➡️ Beispiel 2:

Hier steht 5 – x unter der Wurzel. Also stellst du die Ungleichung auf. Du setzt also den Ausdruck wieder größer oder gleich null:

Dann rechnest du +x auf beiden Seiten, um die Gleichung zu lösen.

Wenn du das x links stehen haben möchtest, drehst du das größer oder gleich null Zeichen um.
 .
.
Die Definitionsmenge lautet also:

In diesem Fall sind alle Zahlen bis 5 erlaubt.
So bestimmst du die Definitionsmenge für Exponentialfunktionen und Logarithmusfunktionen
Exponentialfunktionen
Exponentialfunktionen sind unkompliziert. Egal, welche Zahl du für x einsetzt — der Ausdruck im Exponenten ist immer erlaubt. Deshalb gilt für eine Funktion wie 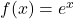 immer die Definitionsmenge
immer die Definitionsmenge
![Rendered by QuickLaTeX.com \[ \mathbb{D} = \mathbb{R} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-eceead57bbbef782b9eb82508c85a2dd_l3.png)
Das bedeutet: x kann jede reelle Zahl annehmen.
Logarithmusfunktionen
Anders sieht es bei Logarithmusfunktionen aus. Hier gibt es eine wichtige Einschränkung: Der Ausdruck in der Klammer des Logarithmus muss größer als null sein. Null oder negative Zahlen sind nicht erlaubt.
➡️ Beispiel:

Hier darf der Ausdruck x – 1 nicht kleiner oder gleich null sein. Du stellst also die Ungleichung auf:

Daraus folgt x > 1. Damit lautet die Definitionsmenge:

Das heißt: x darf jede reelle Zahl sein, solange sie größer als 1 ist. Das kannst du auch am Graphen erkennen.
Gut zu wissen: Die e-Funktion ist die Umkehrfunktion der ln-Funktion. Das bedeutet, dass die Definitionsmenge der e-Funktion der Wertebereich der ln-Funktion ist – und umgekehrt.
So bestimmst du die Definitionsmenge für trigonometrische Funktionen
Sinus und Kosinus
Bei Sinus und Kosinus musst du keine Einschränkungen beachten. Egal, welchen Wert du für x einsetzt — es gibt immer ein Ergebnis. Deshalb gilt:
![Rendered by QuickLaTeX.com \[ \mathbb{D} = \mathbb{R} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-eceead57bbbef782b9eb82508c85a2dd_l3.png)
Tangens
Beim Tangens
sieht es anders aus. Er ist als  definiert. Da der Nenner niemals null werden darf, musst du alle Werte ausschließen, bei denen cos(x)=0 ist. Das ist bei
definiert. Da der Nenner niemals null werden darf, musst du alle Werte ausschließen, bei denen cos(x)=0 ist. Das ist bei

der Fall.
Die Definitionsmenge des Tangens lautet also:
![Rendered by QuickLaTeX.com \[ \mathbb{D} = \mathbb{R} \setminus \left\{ \tfrac{\pi}{2} + k\pi \,\middle|\, k \in \mathbb{Z} \right\} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ac2a903a29ef57b074b995f5c83128b5_l3.png)
Die Definitionslücken siehst du auch nochmal am Graphen.
Das Wichtigste auf einen Blick
Hier findest du eine Übersicht über die Definitionsmengen der wichtigsten Funktionstypen. So kannst du schnell nachschauen, welche Regeln gelten:
| Funktionstyp | Definitionsmenge |
|
Ganzrationale Funktionen |
|
Gebrochenrationale Funktionen
|
|
Wurzelfunktionen
|
|
Exponentialfunktionen
|
|
Logarithmusfunktionen
|
|
Sinus- und Kosinusfunktionen  |
|
Tangensfunktion
|
|
Wertebereich
Neben der Definitionsmenge spielt auch der Wertebereich einer Funktion eine wichtige Rolle. Wie du ihn bestimmst und was es dabei zu beachten gibt, erfährst du in unserem Video dazu.








![Rendered by QuickLaTeX.com \[ \mathbb{D} = \mathbb{R} \setminus \{x \mid \text{Nenner } = 0\} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9cd22a955ba6434270dd05b5b74f25c9_l3.png)
![Rendered by QuickLaTeX.com \[ \mathbb{D} = \{x \in \mathbb{R} \mid x+3 \geq 0\} = [-3,\infty) \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8f1852d02d18b8a502a87d166227d5e7_l3.png)
![Rendered by QuickLaTeX.com \[ \mathbb{D} = \{x \in \mathbb{R} \mid x-1 > 0\} = (1,\infty) \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d5a7b05f089f682f87e844bb48e7e0e4_l3.png)
