Tschebyscheff Ungleichung
Hier erfährst du alles zur Ungleichung von Tschebyscheff. Die dazugehörige Formel wird dir anhand eines anschaulichen Beispiels einfach erklärt.
Du schaust gerne Filme? Wir auch! Unser Video erklärt dir sofort was es mit der Ungleichung von Tschebyscheff auf sich hat.
Inhaltsübersicht
Ungleichung von Tschebyscheff einfach erklärt
Mithilfe der Tschebyscheff Ungleichung kann die maximale Wahrscheinlichkeit geschätzt werden, dass der Wert einer Zufallsvariable X sich außerhalb bestimmter Intervallgrenzen befindet. Die sich ergebende Wahrscheinlichkeit ist eine obere Abschätzung. Sie wird das errechnete Ergebnis also nicht übersteigen, kann aber darunter liegen.
Alternativ kann auch die Gegenwahrscheinlichkeit als untere Abschätzung bestimmt werden, also die Mindestwahrscheinlichkeit, dass der Wert einer Zufallsvariable  sich innerhalb der Intervallgrenzen befindet.
sich innerhalb der Intervallgrenzen befindet.
Tschebyscheff Ungleichung Formel
Schauen wir uns nun zunächst die Formel für die Tschebyscheff Ungleichung an. Diese lautet:
Ungleichung 1: 
Wobei  für den Erwartungswert steht,
für den Erwartungswert steht,  die Varianz (Zur Erinnerung: V(X) äquivalent zu
die Varianz (Zur Erinnerung: V(X) äquivalent zu  ) bezeichnet und
) bezeichnet und  die Breite des Intervalls bestimmt.
die Breite des Intervalls bestimmt.
Äquivalent zu Ungleichung 1 kann aber auch die folgende alternative Darstellung verwendet werden.
Ungleichung 2: 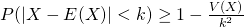
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Tschebyscheff Ungleichung Erklärung
Mit der Ungleichung 1 kann die obere Wahrscheinlichkeit (Maximalwahrscheinlichkeit) dafür geschätzt werden, dass der Wert einer Zufallsvariable X außerhalb des durch k und den Erwartungswert E(X) definierten Intervalls liegt.
Mit anderen Worten: es wird die Wahrscheinlichkeit P gesucht, dass

Mit der Ungleichung 2 kann man die entsprechende Gegenwahrscheinlichkeit bestimmen, also die untere Wahrscheinlichkeit (Minimalwahrscheinlichkeit). Es wird geschätzt, dass der Wert einer Zufallsvariable  innerhalb des durch
innerhalb des durch  und den Erwartungswert definierten Intervalls liegt. Anders beschrieben wird die Wahrscheinlichkeit
und den Erwartungswert definierten Intervalls liegt. Anders beschrieben wird die Wahrscheinlichkeit  gesucht, dass
gesucht, dass

Aus Gründen der Vereinfachung werden wir im nun folgenden Beispiel ausschließlich auf Ungleichung 1 eingehen. Die Berechnung der Gegenwahrscheinlichkeit mithilfe von Ungleichung 2 erfolgt äquivalent.
Tschebyscheff Ungleichung Beispiel
Zur Veranschaulichung erläutern wir die Funktionsweise der Ungleichung von Tschebyscheff anhand eines Binnenschiffes, welches einen großen Fluss befährt. Das Schiff sollte sich im Optimalfall möglichst in der Mitte des Flusses befinden, um nicht dem Risiko ausgesetzt zu sein auf Grund zu laufen. Die Fahrrinne ist jeweils nach links und rechts begrenzt.
Mit der Formel der Tschebyscheff Ungleichung kann man jetzt die maximale Wahrscheinlichkeit bestimmen, ob sich das Schiff außerhalb der Fahrrinne befindet.
Tschebyscheff Ungleichung Aufgaben: Beispiel Rechnung
Verdeutlichen wir den Sachverhalt anhand eines Rechenbeispiels. Im Erwartungswert sollte sich das Schiff in der Mitte des Flusses aufhalten und damit eine Abweichung von der Flussmitte von 0 haben.
Daraus ergibt sich 
Die Fahrrinne ist 20 m breit, also 10 m in jede Richtung. Daraus ergibt sich  . Die Varianz
ist gegeben und beträgt
. Die Varianz
ist gegeben und beträgt  . Durch Einsetzen erhalten wir:
. Durch Einsetzen erhalten wir:
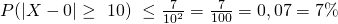
Die Wahrscheinlichkeit, dass sich das Schiff außerhalb der Fahrrinne befindet, also um mehr als 10 m in die eine oder andere Richtung vom Erwartungswert (Flussmittelpunkt) entfernt ist, liegt damit bei 7%.
Tschebyscheff Ungleichung Aufgaben: Beispiel umgekehrte Rechnung
Es kann vorkommen, dass bei bestimmten Aufgaben nur die Wahrscheinlichkeit bekannt ist, mit der dein Zufallsvariablenwert die Grenzen verletzt, aber nicht die Größe der Grenzen. Demzufolge ist  unbekannt und muss bestimmt werden. In diesem Beispiel ist also die Breite der Fahrrinne gesucht.
unbekannt und muss bestimmt werden. In diesem Beispiel ist also die Breite der Fahrrinne gesucht.
Es wird davon ausgegangen, dass die Varianz mit  und der Erwartungswert mit
und der Erwartungswert mit  unverändert zur vorherigen Aufgabe sind. Die Wahrscheinlichkeit, dass der Wert deiner Zufallsvariable sich außerhalb des Intervalls befindet, ist mit 10 % angegeben. Mithilfe der Tschebyscheff Ungleichung ergibt sich daraus folgende Rechnung:
unverändert zur vorherigen Aufgabe sind. Die Wahrscheinlichkeit, dass der Wert deiner Zufallsvariable sich außerhalb des Intervalls befindet, ist mit 10 % angegeben. Mithilfe der Tschebyscheff Ungleichung ergibt sich daraus folgende Rechnung:


Um mit einer Wahrscheinlichkeit von 10 % die Fahrrinne zu verlassen, müsste die Fahrrinne laut Tschebyscheff Ungleichung also eine Abweichung von weniger als  zulassen. Die Fahrrinne ist also insgesamt 16,74 m breit.
zulassen. Die Fahrrinne ist also insgesamt 16,74 m breit.
Tschebyscheff Ungleichung Beweis
Es ist möglich, die tschebyscheffsche Ungleichung mithilfe der Markow-Ungleichung herzuleiten.
Markow-Ungleichung: ![Rendered by QuickLaTeX.com \ P[Y\geq k]\leq \frac{E[h(Y)]}{h(k)}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-812304f79924117f50256830743146bb_l3.png)
Häufig wird die Ungleichung von Tschebyscheff daher als Sonderfall der Markow-Ungleichung beschrieben.
Tschebyscheff Ungleichung Variante Standardabweichung
Eine zusätzliche, häufig zitierte Variante der Tschebyscheff Ungleichung ist die Folgende:

Dabei ergibt sich die Standardabweichung aus der Wurzel der Varianz:



