Kombinatorik
Du fragst dich wie du Aufgaben zur Kombinatorik lösen kannst? Hier bekommst du eine Übersicht und lernst wann du welche Formel verwenden musst.
Nach unserem Video zur Kombinatorik ist die Berechnung der Anzahl der Anordnungsmöglichkeiten bei Permutationen, Variationen und Kombinationen kein Problem mehr für Dich!
Inhaltsübersicht
Kombinatorik einfach erklärt
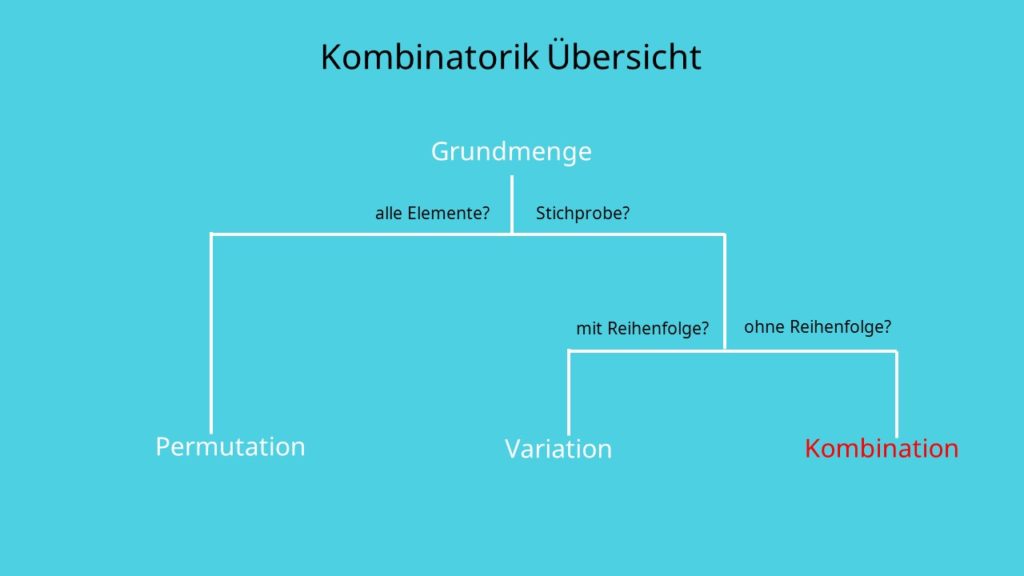
Einfach gesagt hilft dir die Kombinatorik dabei die Anzahl der möglichen Anordnungen von Objekten zu bestimmen. Innerhalb der abzählenden Kombinatorik gibt es Permutationen, Variationen und Kombinationen. In erster Linie musst du unterscheiden, ob man alle Elemente der Grundmenge betrachtet oder nicht. Falls ja, handelt es sich um eine Anordnung, also eine Permutation. Handelt es sich um eine Stichprobe, hast du es mit einer Auswahl zu tun und unterscheidest zwischen Variationen und Kombinationen. Spielt die Reihenfolge eine Rolle, ist es eine Variation, falls nicht ist es eine Kombination. Bei jedem der drei Fälle gibt es dann noch die beiden Möglichkeiten mit oder ohne Wiederholung. Wiederholung heißt, ob die Elemente unterscheidbar sind oder nicht beziehungsweise, ob du die Elemente nach dem Ziehen zurück legst.
Kombinatorik Formeln
Wie bereits gesagt ist das Ziel in der Kombinatorik die Anzahl der möglichen Anordnungen zu bestimmen. Für diese Berechnungen brauchst du verschiedene Formeln bei Permutationen, Kombinationen und Variationen. Je nachdem, wo wir uns nach dieser Unterscheidung befinden, gibt es eine andere Formel zur Berechnung. Das n in den Formeln steht immer für die Anzahl aller Elemente, also für die Grundgesamtheit. Das k gibt die Anzahl an Ziehungen an. Daher kommen auch die Begriffe k-Tupel, k-Mengen, k-Permutation oder k-Kombination, welche ganz einfach eine Aufzählung der Objekte im jeweiligen Fall beschreiben. Je nach Fall sind auch die Fakultät oder der Binomialkoeffizient relevant für die Berechnung. Um herauszufinden, welche Formel du verwenden musst, stellst du dir am besten folgende Fragen:
- Betrachte ich alle Elemente oder nur eine Stichprobe?
- Spielt die Reihenfolge eine Rolle?
- Können die Elemente mit Wiederholung vorkommen?
Die folgende Grafik liefert dir einen Überblick, welche Formel du wann verwenden musst.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Kombinatorik Tabelle
Hier hast du nochmal alle Formeln auf einen Blick. Tabellarisch dargestellt sieht das Ganze dann so aus:
| ohne Wiederholung | mit Wiederholung | |
| Permutation |
|
|
| Variation |
|
|
| Kombination |
|
|
Kombinatorik Permutation
Wie du inzwischen weißt, gilt bei Permutationen allgemein, dass du alle Elemente der Grundgesamtheit beachten musst. Es gilt also n = k. Das heißt, dass du also alle vorhandenen Objekte berücksichtigst. Auch die Reihenfolge wird hier immer berücksichtigt. Was genau das bedeutet wird klarer, wenn wir uns die beiden Fälle mit oder ohne Wiederholung anschauen.
Permutation ohne Wiederholung
Hier handelt es sich um die Anordnung von Objekten, welche alle verschieden sind. Das Ziel ist es, alle Objekte in einer bestimmten Reihenfolge anzuordnen. Zu Beginn sind noch alle Plätze frei. Für das zweite Objekt verbleiben jedoch nur noch (n-1) Möglichkeiten, für das dritte analog dann (n-2) und so weiter….Führst du diese Reihe fort, so ergibt sich die Fakultät, also die Formel zur Berechnung der Anzahl der Möglichkeiten: n!
Beispiel Permutation ohne Wiederholung: Hast du zum Beispiel 3 gute Freunde und sollst ein Ranking bilden, wen du am liebsten magst, dann solltest du auch alle 3 in deiner Liste berücksichtigen und dich nicht nur zwischen zweien entscheiden. Hier handelt es sich um eine Permutation ohne Wiederholung, wobei mit ohne Wiederholung gemeint ist, dass du deine Freunde voneinander unterscheiden kannst und keiner „wiederholt“ vorkommt. Fachlich ausgedrückt sagt man, dass alle Objekte der Menge verschieden sind und dadurch kein Objekt mit den gleichen Merkmalen zwei mal vorkommen kann. Ein weiteres Beispiel zu Permutationen ohne Wiederholung findest du in unserem gleichnamigen Video!
Permutation mit Wiederholung
Im Falle einer Permutation mit Wiederholung sind nicht mehr alle Objekte voneinander unterscheidbar. Es kann also vorkommen, dass sich die Reihenfolge an sich nicht ändert, auch wenn zwei Objekte mit den gleichen Merkmalen getauscht werden. Man kann dabei Gruppen bilden, welche die Objekte mit gleichen Merkmalen zusammenfassen. Die Anzahl der Möglichkeiten wird dann mit der Formel  berechnet.
berechnet.
Beispiel Permutation mit Wiederholung: Du hast insgesamt 9 Gummibärchen: 2 rote, 4 gelbe und 3 grüne Exemplare. Du könntest also zuerst alle roten, dann alle gelben und zum Schluss alle grünen Bärchen essen. Dabei spielt es keine Rolle, ob du zuerst den einen oder den anderen roten Bären isst, da du diese sowieso nicht unterscheiden kannst. MitWiederholung ist hier nicht gemeint, dass du ein Bärchen ableckst und dann wieder zurücklegst, sondern eben die Tatsache, dass sich verschiedene „Gruppen“ in der Tüte befinden. Die Anzahl deiner Gummibärchenspeisepläne kannst du also folgendermaßen berechnen:  . Auch zu Permutationen mit Wiederholung
haben wir in dem dazugehörigen Video ein weiteres anschauliches Beispiel für dich!
. Auch zu Permutationen mit Wiederholung
haben wir in dem dazugehörigen Video ein weiteres anschauliches Beispiel für dich!
Variation ohne Wiederholung
Betrachtet man den Fall ohne Wiederholung, muss dir bewusst sein, dass jedes Objekt nur einmal vorkommt, beziehungsweise, dass das Objekt nicht zurück gelegt werden darf. Daraus ergibt sich, dass es für das erste Objekt noch n Plazierungsmöglichkeiten gibt. Für das zweite bleiben dann noch (n-1) und so weiter. Für das letzte Objekt bleiben dann noch (n-k+1) Möglichkeiten. Du erhältst also du folgende Formel:
 …
… 
Kombinatorik Beispiel Variation ohne Wiederholung:
Ein anschauliches Beispiel hierfür ist, wie viele Möglichkeiten es gibt die ersten drei Plätze bei einem Turnier mit mehreren Gruppen zu besetzen. Hier macht es nämlich natürlich einen Unterschied, ob eine Gruppe auf dem ersten oder auf dem dritten Platz landet. Wir betrachten also eine Variation ohne Wiederholung. Genau dieses Szenario berechnen wir in unserem Video Ziehen ohne Zurücklegen mit Reihenfolge !
Variation mit Wiederholung
In diesem Fall können Objekte auch mehrmals ausgewählt werden. Das heißt also, dass manche nicht unterscheidbar sind. Das kann auch der Fall sein, wenn du das Objekt nach der Auswahl wieder zu den anderen Elementen zurück legst. Wieder gibt es für das erste Objekt n Auswahlmöglichkeiten. Aufgrund der Mehrfachauswahl gilt das aber auch für alle weiteren Objekte. Du rechnest also  …
… 
Kombinatorik Beispiel Variation mit Wiederholung:
Ein anschauliches Beispiel hierfür ist der Code eines Fahrradschlosses. Die Reihenfolge der Zahlen macht einen Unterschied, allerdings kann jede Zahl beliebig oft vorkommen. Überträgt man das Ganze auf ein Urnenmodell, dann handelt es sich um Ziehungen mit Zurücklegen, bei denen die Reihenfolge einen Unterschied macht. Du hast es also mit einer Variation mit Wiederholung zu tun. Auch hier bleiben nach dem Video Ziehen mit Zurücklegen mit Reihenfolge keine Fragen mehr offen.
Kombination ohne Wiederholung
Hast du ein Objekt nun einmal ausgewählt, so kann dieses nicht wieder vorkommen. Es können also die ausgewählten Objekte k nur auf k! verschiedene Plätze verteilt werden. Mit der Formel für Variationen ohne Wiederholung im Hinterkopf kannst du dir ganz einfach die Formel für diesen Fall herleiten, welche dann folgendermaßen aussieht:

Dieser Ausdruck ist auch als n über k, oder eben als Binomialkoeffizient bekannt.
Kombinatorik Beispiel Kombination ohne Wiederholung:
Am einfachsten ist es, wenn du dir hierzu wieder ein Urnenmodell vorstellst. Wir haben eine Kiste mit 8 schwarzen und 4 weißen Kugeln. Jetzt ziehen wir 4 Kugeln und legen diese nicht wieder zurück. Die Reihenfolge ist dir egal. Auch zu Kombination ohne Wiederholung bleiben nach unserem Video Ziehen ohne Zurücklegen ohne Reihenfolge keine Fragen mehr offen.
Kombination mit Wiederholung
Du hast es mit dem Szenario zu tun, dass die Reihenfolge der Ergebnisse des Zufallsexperimentes keine Rolle spielt und das Ergebnis erneut eintreten kann, wenn es bereits aufgetreten ist. Schaue dir nochmal die Formel für den Fall ohne Wiederholung an. Passen wir die Formel anhand dieser Anforderungen an, so ergibt sich folgende Formel:

Kombinatorik Beispiel Kombination mit Wiederholung:
Stell dir dazu wieder das Urnenmodell vor. Du ziehst also die Kugeln aus der Urne und legst sie nach jedem Zug wieder zurück. Es handelt sich also um eine Kombination mit Wiederholung. Um dein Wissen zu allen verschiedenen Fällen komplett zu machen, hilft dir unser Video Ziehen mit Zurücklegen ohne Reihenfolge weiter.
Kombinatorik Aufgaben
In der Theorie klingt das alles einleuchtend, aber wie sieht es mit dem Lösen konkreter Aufgaben aus? Übung macht den Meister! Merke dir am besten alle Kombinatorik Formeln oder schreibe sie dir in deine Formelsammlung. Bevor du loslegen kannst, ist es wichtig, dass du dich mit den Basics zum Binomialkoeffizient, der Fakultät und dem Urnenmodell auskennst. Mit den Hilfsfragen vom Anfang kannst du dann für jede Aufgabe ganz leicht erkennen, welche Formel du verwenden musst, um auf die richtige Lösung zu kommen.
Binomialkoeffizient und Fakultät
Damit auch bei der Berechnung mit den Formeln nichts schief geht, beginnen wir mit einem kurzen Exkurs zum Binomialkoeffizient und der Fakultät. Diese sind zwei zentrale Elemente in der Kombinatorik, an welchen du bei der Berechnung der Auswahl und Anordnungsmöglichkeiten nicht vorbei kommst.
Fakultät:
Die Fakultät wird als n! notiert und lässt sich ermitteln, indem man alle natürlichen Zahlen von 1 bis n miteinander multipliziert. Eine alternative Schreibweise ist also auch 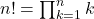 .
.
Binomialkoeffizient: Der Binomialkoeffizient wird auch als n über k oder k aus n bezeichnet und ist dir vielleicht auch schon in der Formel der Binomialverteilung begegnet. Es gibt eine Kurzschreibweise und eine ausgeschriebene Version der Formel.

n über k setzt sich zusammen aus der Fakultät von n, geteilt durch die Fakultät von k, multipliziert mit der Fakultät von n-k.
Urnenmodell
Typische Aufgaben in der Kombinatorik sind Zufallsexperimente mit Urnenmodellen. Man verwendet dazu eine Kiste, einen Beutel oder eben eine Urne, in der sich verschiedene Kugeln befinden. Nun werden aus dem Behälter, ohne hineinzusehen, Kugeln gezogen und es wird notiert, welche Farbe diese haben. Dabei gibt es verschiedene Varianten wie dieses Zufallsexperiment durchgeführt wird. Man unterscheidet, ob eine gezogene Kugel wieder zurückgelegt wird und ob die Reihenfolge eine Rolle spielt oder nicht. Das Urnenmodell wird oft verwendet, um Alltagssituationen vereinfacht darzustellen und Wahrscheinlichkeiten leichter berechnen zu können. In unserer Kombinatorik Playlist haben wir für jeden Fall ein anschauliches Beispiel für dich!
Kombinatorik Aufgaben mit Lösungen
Jetzt bist du dran! Im Folgenden kannst du testen, ob du in einem ersten Schritt auf den richtigen Lösungsweg und in einem zweiten Schritt auf die richtige Lösung kommst.
Aufgabe :
Du hast den Code für dein Handy vergessen. Wie viele Möglichkeiten gibt es, wenn du zumindest noch weißt, dass dein Code 4 Zeichen lang war?
Lösung 1:
- Betrachte ich alle Elemente oder nur eine Stichprobe?
Man betrachtet nur eine Stichprobe, da du ja von den 10 möglichen Ziffern von 0-9 nur 4 auswählst. - Spielt die Reihenfolge eine Rolle?
Die Reihenfolge spielt logischerweise eine Rolle, da du nur so dein Handy entsperren kannst. - Können die Elemente mit Wiederholung vorkommen?
Ja, du kannst rein theoretisch auch 1111 als Code verwenden. Nicht clever, aber möglich.
Folgst du dem Lösungsbaum, gelangst du zu folgender Formel  und der dazugehörigen Lösung mit
und der dazugehörigen Lösung mit 
Aufgabe 2:
Stell dir nun vor, dass du vor dir einen Teller Buchstabensuppe hast. Du siehst, dass in deinem Teller noch genau die Buchstaben schwimmen, um das Wort Mississippi zu bilden. Wie viele Möglichkeiten hast du die Buchstaben anzuordnen?
Lösung 2:
- Betrachte ich alle Elemente oder nur eine Stichprobe?
Du betrachtest alle Elemente, da du ja in deinem neuen Wort (welches nicht unbedingt einen Sinn haben muss) auch alle Buchstaben verbauen willst. - Spielt die Reihenfolge eine Rolle? Ja die Reihenfolge spielt eine Rolle, da Mississippi offensichtlich etwas anderes als Pipimississ ist.
- Können die Elemente mit Wiederholung vorkommen?
Hier wird es knifflig. Es handelt sich hier nicht etwa um ein Urnenmodell mit Zurücklegen, aber deine Elemente können trotzdem wiederholt vorkommen! Du musst also wissen, dass es keinen Unterschied macht, ob du zuerst das erste oder das zweite s verwendest. Innerhalb des Wortes kannst du diese nicht unterscheiden! Du benutzt zur Berechnung also folgende Formel  und kommst auf dieses Ergebnis
und kommst auf dieses Ergebnis 


![Rendered by QuickLaTeX.com \[n!\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-42dee5a3fb4bd7ea51f1e8dd2a3c18bf_l3.png)
![Rendered by QuickLaTeX.com \[\frac{n!}{k_1!\cdot k_2!\cdots k_n!}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f7d17bb905615b310b6d9a8843b391d7_l3.png)
![Rendered by QuickLaTeX.com \[\frac{n!}{(n-k)!}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-21616eb86344b64a21bea319cd8b30ca_l3.png)
![Rendered by QuickLaTeX.com \[n^k\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-967415464ef9a4db6121d96d92cb1f53_l3.png)
![Rendered by QuickLaTeX.com \[\frac{n!}{k!\cdot(n-k)!}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-84ec2cddbf513cc0d88387672f83e75c_l3.png)
![Rendered by QuickLaTeX.com \[\frac{(n+k-1)!}{(n-1)!\cdot k!}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-db95ab34d2fab18d59a9982acf1691d6_l3.png)