Definitionsbereich
Du fragst dich, was es mit dem Definitionsbereich auf sich hat und wie man ihn für verschiedene Funktionen bestimmt? Hier erklären wir es dir leicht verständlich und mit vielen Beispielen. Wenn dir die anschauliche Version lieber ist und du direkt sehen willst, wie du den Definitionsbereich bestimmen kannst, dann schau dir unser Video an!
Inhaltsübersicht
Definitionsbereich einfach erklärt
In eine Funktion
, zum Beispiel in  , kannst du verschiedene Zahlen einsetzen und es kommen unterschiedliche Funktionswerte
heraus. Bei manchen Funktionen darfst du einfach jede beliebige Zahl einsetzen — manchmal sind aber einige Zahlen nicht erlaubt.
, kannst du verschiedene Zahlen einsetzen und es kommen unterschiedliche Funktionswerte
heraus. Bei manchen Funktionen darfst du einfach jede beliebige Zahl einsetzen — manchmal sind aber einige Zahlen nicht erlaubt.
Wenn du den Definitionsbereich einer Funktion bestimmst, beantwortest du die Frage:
Welche x-Werte darf ich in die Funktion einsetzen?
Schau dir dazu ein Beispiel an: In die Funktion  darfst du alle Zahlen einsetzen außer x = 0. Für x = 0 würde nämlich
darfst du alle Zahlen einsetzen außer x = 0. Für x = 0 würde nämlich  dastehen, du würdest also 1 durch 0 teilen — und das darfst du nicht! Deshalb ist der maximale Definitionsbereich „alle Zahlen außer 0„. Die 0 nennst du dann Definitionslücke.
dastehen, du würdest also 1 durch 0 teilen — und das darfst du nicht! Deshalb ist der maximale Definitionsbereich „alle Zahlen außer 0„. Die 0 nennst du dann Definitionslücke.
Übrigens: Alle Zahlen, die bei einer Funktion als y-Werte herauskommen können, nennst du Wertebereich
. Der Wertebereich von  ist also „alle Zahlen außer 1“ .
ist also „alle Zahlen außer 1“ .
Je nach Art der Funktion bestimmst du die Zahlen, die in die Funktion eingesetzt werden können, auf unterschiedliche Weise. Wie genau, erfährst du jetzt!
Definitionsbereich bestimmen
Für den Definitionsbereich schaust du dir an, welche Zahlen du in deine Funktion einsetzen darfst. Oft kannst du diese Zahlenmengen mit Symbolen darstellen. Die wichtigsten Zahlenmengen findest du hier:
| natürliche Zahlen |  |
{1; 2; 3; …} |
| ganze Zahlen |  |
{… ; -2; -1; 0; 1; 2; 3; …} |
| rationale Zahlen |  |
 |
| reelle Zahlen |  |
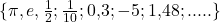 |
Aber wie kannst du die Zahlen herausfinden, die du in eine Funktion einsetzen darfst? Dazu musst du dir immer deine konkrete Funktion anschauen, denn für verschiedene Funktionstypen gibt es verschiedene Regeln.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Ganzrationale Funktionen
Bei ganzrationalen Funktionen musst du dir nicht viele Gedanken machen:
Ganzrationale Funktion haben den Definitionsbereich  . Du darfst also jede Zahl in eine ganzrationale Funktion einsetzen.
. Du darfst also jede Zahl in eine ganzrationale Funktion einsetzen.
Zu den ganzrationalen Funktionen zählen
- lineare Funktionen wie f(x) = 2x + 5 oder f(x) = x – 3
- quadratische Funktionen wie f(x) = x2 + 2x + 4
- alle anderen Polynome wie f(x) = x4 – 6x2 + 5x
Hier ist der Definitionsbereich immer der gleiche: Du darfst alle reellen Zahlen einsetzen!
Schon gewusst? Eine Ausnahme ist dabei natürlich, wenn der Definitionsbereich von vornherein eingeschränkt wird. Dann betrachtest du beispielsweise f(x) nur auf dem Intervall [a,b]. Das findet insbesondere bei abschnittsweise definierten Funktionen oder in der Integralrechnung Anwendung.
Gebrochen rationale Funktion
Anders sieht es bei gebrochen rationalen Funktionen
aus. Das sind Funktionen mit einem Bruch, bei denen im Nenner (also unten im Bruch) ein x vorkommt: zum Beispiel  oder
oder  .
.
- Schritt 1: Berechne die Nullstellen des Nenners.
-
Schritt 2: Schreibe den Definitionsbereich
 auf. Das \ steht für „ohne“ :
auf. Das \ steht für „ohne“ :  ist also die reellen Zahlen ohne die Nullstellen des Nenners.
ist also die reellen Zahlen ohne die Nullstellen des Nenners.

Die Nullstellen des Nenners darfst du also nicht in die Funktion einsetzen. Wenn du nämlich eine der Nullstellen einsetzt, kommt ja im Nenner 0 heraus und du würdest durch 0 teilen — und das darfst du in der Mathematik nicht!
Beispiel 1
Du sollst den Definitionsbereich der Funktion  bestimmen. Um die Definitionslücken zu ermitteln, berechnest du die Nullstellen des Nenners:
bestimmen. Um die Definitionslücken zu ermitteln, berechnest du die Nullstellen des Nenners:

Die beiden Definitionslücken sind somit x1 = -2 und x2 = 2. Du kannst also den Definitionsbereich angeben:

Das siehst du auch direkt, wenn du den Graphen von  zeichnest. Der Funktionsgraph hat bei
zeichnest. Der Funktionsgraph hat bei  und bei
und bei  jeweils eine senkrechte Asymptote
, an die der Graph sich nach oben und unten hin immer mehr annähert.
jeweils eine senkrechte Asymptote
, an die der Graph sich nach oben und unten hin immer mehr annähert.
Beispiel 2
Wir wollen den Definitionsbereich von 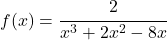 bestimmen. Dazu berechnest du wieder zuerst die Definitionslücken, das heißt die Nullstellen des Nenners.
bestimmen. Dazu berechnest du wieder zuerst die Definitionslücken, das heißt die Nullstellen des Nenners.
x3 + 2x2 – 8x = 0
Dafür klammerst
du ein x aus. Dann steht in der Klammer eine quadratische Funktion
, die du mit der Mitternachtsformel
lösen kannst. Du erhältst also:
x(x2 + 2x – 8) = 0
⇒ x1 = 0, x2 = 2 und x3 = -4
Für den Definitionsbereich gilt also  Der Funktionsgraph sieht hier folgendermaßen aus.
Der Funktionsgraph sieht hier folgendermaßen aus.
E Funktion und ln-Funktion
Auch bei der e-Funktion
und der ln-Funktion
 gibt es einige Besonderheiten.
gibt es einige Besonderheiten.
- Die e-Funktion hat den Definitionsbereich
 . Du darfst also alle reellen Zahlen einsetzen.
. Du darfst also alle reellen Zahlen einsetzen. - Die ln-Funktion ln(x) hat den Definitionsbereich
 . Im ln dürfen also nur positive Zahlen stehen!
. Im ln dürfen also nur positive Zahlen stehen!
Achtung: Bei komplizierteren ln-Ausdrücken ist der Definitionsbereich meist nicht einfach  ! Schau dir dazu ein Beispiel an:
! Schau dir dazu ein Beispiel an:
Angenommen, du möchtest den Definitionsbereich von  angeben. Weil du in den ln nur positive Zahlen einsetzen darfst, muss hier das Innere der Funktion, das heißt
angeben. Weil du in den ln nur positive Zahlen einsetzen darfst, muss hier das Innere der Funktion, das heißt  , positiv sein. Dann gehst du so vor:
, positiv sein. Dann gehst du so vor:
-
Schritt 1: Berechne die Nullstellen der inneren Funktion:

-
Schritt 2: Finde heraus, wann
 und wann
und wann  ist. Dafür kannst du dir zum Beispiel den Graphen von
ist. Dafür kannst du dir zum Beispiel den Graphen von  anschauen.
anschauen.
Du siehst, dass  im Intervall
im Intervall ![Rendered by QuickLaTeX.com [\textcolor{red}{-2,2}]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8ecf9b3a08f258943365eb31e23525fa_l3.png) negativ ist und sonst positiv. Alle Zahlen, für die
negativ ist und sonst positiv. Alle Zahlen, für die  positiv ist, bilden jetzt deinen Definitionsbereich der ln-Funktion:
positiv ist, bilden jetzt deinen Definitionsbereich der ln-Funktion:

Das  -Zeichen ist ein „und„. Du darfst also alles einsetzen von minus unendlich bist -2 und alles von 2 bis plus unendlich! Die runden Klammern sagen dir, dass du auch die 2 und die -2 nicht einsetzen darfst.
-Zeichen ist ein „und„. Du darfst also alles einsetzen von minus unendlich bist -2 und alles von 2 bis plus unendlich! Die runden Klammern sagen dir, dass du auch die 2 und die -2 nicht einsetzen darfst.
Wurzelfunktion
Auch in die Wurzelfunktion
 darfst du nicht alle x-Werte einsetzen.
darfst du nicht alle x-Werte einsetzen.
Die Wurzelfunktion hat den Definitionsbereich  . Du darfst also alle positiven Zahlen und die 0 einsetzen.
. Du darfst also alle positiven Zahlen und die 0 einsetzen.
Achtung: Für kompliziertere Wurzel-Funktionen gibt es noch mehr zu beachten. Schau dir das Vorgehen am Beispiel an:
Gesucht sind alle Zahlen, die du in  einsetzen darfst. Das ist eine sehr steile Wurzelfunktion, deren Graph um 2 nach rechts in x-Richtung verschoben ist.
einsetzen darfst. Das ist eine sehr steile Wurzelfunktion, deren Graph um 2 nach rechts in x-Richtung verschoben ist.
-
Schritt 1: Berechne die Nullstellen des Ausdrucks unter der Wurzel:
![Rendered by QuickLaTeX.com \begin{align*} x^3-8 &= 0 &|+8 \\ x^3 &=8 &|\sqrt[3]{...} \\ x &=2 \end{align*}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-4dd150c4ffa0e8544d1bd95637aa485f_l3.png)
-
Schritt 2: Finde heraus, wann
 positiv ist und wann negativ. Dafür schaust du dir den Graphen von
positiv ist und wann negativ. Dafür schaust du dir den Graphen von  an. Daran siehst du, dass
an. Daran siehst du, dass  für
für  positiv ist.
positiv ist.
- Schritt 3: Definitionsbereich angeben:

Schon gewusst? Etwas aufpassen musst du, wenn du die n-ten Wurzeln ![Rendered by QuickLaTeX.com \sqrt[n]{f(x)}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-825f54cd8afb4c11469f67f39559bd79_l3.png) untersuchst. Ist n ungerade, also zum Beispiel
untersuchst. Ist n ungerade, also zum Beispiel ![Rendered by QuickLaTeX.com \sqrt[\textcolor{orange}{3}]{f(x)}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3bd57a5f2768e6e86964e4b52660ceaf_l3.png) , so sind negative Ausdrücke unter der Wurzel erlaubt und du darfst jede reelle Zahl einsetzen. (
, so sind negative Ausdrücke unter der Wurzel erlaubt und du darfst jede reelle Zahl einsetzen. ( ). Für gerades n, also zum Beispiel für
). Für gerades n, also zum Beispiel für ![Rendered by QuickLaTeX.com \sqrt[\textcolor{teal}{4}]{f(x)}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f74a0b22350623cd83d05cdad4d691fe_l3.png) ergibt der Ausdruck keinen Sinn, sobald
ergibt der Ausdruck keinen Sinn, sobald  ist. Der Definitionsbereich ist somit
ist. Der Definitionsbereich ist somit  .
.
Trigonometrische Funktionen
Manchmal musst du bei trigonometrischen Funktionen angeben, welche Zahlen du einsetzen darfst. Bei Sinus und Cosinus ist das jeweils kein Problem:
-
 hat den Definitionsbereich
hat den Definitionsbereich 
-
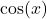 hat den Definitionsbereich
hat den Definitionsbereich 
Das siehst du auch direkt an den beiden Funktionsgraphen:
Betrachtest du nun den Tangens , so ist die Sache etwas komplizierter, da
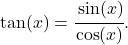
Die Definitionslücken sind daher alle Nullstellen der Cosinusfunktion, d. h. bei allen  mit
mit  . Diese erkennst du am Graphen: Es sind die Werte
. Diese erkennst du am Graphen: Es sind die Werte  ,
, 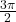 ,
,  usw. Somit ergibt sich für den Definitionsbereich:
usw. Somit ergibt sich für den Definitionsbereich:

Bei Umkehrfunktionen
sind Wertebereich und Definitionsbereich immer vertauscht. Weil der Wertebereich von  und
und 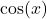 das Intervall
das Intervall ![Rendered by QuickLaTeX.com [-1, 1]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c7eedfc68f155bcb4cde8057b5e7740f_l3.png) ist, gilt für die Umkehrfunktionen:
ist, gilt für die Umkehrfunktionen:
 und
und  haben den Definitionsbereich
haben den Definitionsbereich ![Rendered by QuickLaTeX.com \mathbb{D}=[-1, 1]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-eee98566fdcbe474b53335608fb52e59_l3.png) .
.
Zusammengefasst findest du die Definitionsbereiche der trigonometrischen Funktionen nochmals in dieser Tabelle:
| Funktion | Definitionsbereich |
| sin(x) |  |
| cos(x) |  |
| tan(x) |  |
| arcsin(x) = sin-1(x) |
 = [-1,1] = [-1,1] |
| arccos(x) = cos-1(x) |
 = [-1,1] = [-1,1] |
Wertebereich
Der Definitionsbereich gibt an, welche Werte du für x in eine Funktion einsetzen darfst. Im Gegensatz dazu ermittelst du für den Wertebereich die Menge aller möglichen y-Werte einer Funktion. Auch dazu haben wir ein eigenes Video für dich. Schau es dir gleich an!








